Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Scott, R. K.
and
Tissier, A.-S.
2012.
The generation of zonal jets by large-scale mixing.
Physics of Fluids,
Vol. 24,
Issue. 12,
Parker, Jeffrey B.
and
Krommes, John A.
2013.
Zonal flow as pattern formation.
Physics of Plasmas,
Vol. 20,
Issue. 10,
Bakas, Nikolaos A.
and
Ioannou, Petros J.
2013.
Emergence of Large Scale Structure in Barotropicβ-Plane Turbulence.
Physical Review Letters,
Vol. 110,
Issue. 22,
Bakas, Nikolaos A.
and
Ioannou, Petros J.
2013.
On the Mechanism Underlying the Spontaneous Emergence of Barotropic Zonal Jets.
Journal of the Atmospheric Sciences,
Vol. 70,
Issue. 7,
p.
2251.
Dritschel, David G.
2013.
Waves and Turbulence: Their Cooperative Role in Structure Formation.
Procedia IUTAM,
Vol. 8,
Issue. ,
p.
85.
Constantinou, Navid C.
Farrell, Brian F.
and
Ioannou, Petros J.
2014.
Emergence and Equilibration of Jets in Beta-Plane Turbulence: Applications of Stochastic Structural Stability Theory.
Journal of the Atmospheric Sciences,
Vol. 71,
Issue. 5,
p.
1818.
Verhoeven, Jan
and
Stellmach, Stephan
2014.
The compressional beta effect: A source of zonal winds in planets?.
Icarus,
Vol. 237,
Issue. ,
p.
143.
Harnik, Nili
Dritschel, David G.
and
Heifetz, Eyal
2014.
On the equilibration of asymmetric barotropic instability.
Quarterly Journal of the Royal Meteorological Society,
Vol. 140,
Issue. 685,
p.
2444.
Zhang, Y.
and
Afanasyev, Y. D.
2014.
Beta-plane turbulence: Experiments with altimetry.
Physics of Fluids,
Vol. 26,
Issue. 2,
Turner, M. R.
2014.
Temporal evolution of vorticity staircases in randomly strained two-dimensional vortices.
Physics of Fluids,
Vol. 26,
Issue. 11,
Parker, Jeffrey B
and
Krommes, John A
2014.
Generation of zonal flows through symmetry breaking of statistical homogeneity.
New Journal of Physics,
Vol. 16,
Issue. 3,
p.
035006.
Dritschel, David G.
Qi, Wanming
and
Marston, J. B.
2015.
On the late-time behaviour of a bounded, inviscid two-dimensional flow.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
1.
Read, P. L.
Jacoby, T. N. L.
Rogberg, P. H. T.
Wordsworth, R. D.
Yamazaki, Y. H.
Miki-Yamazaki, K.
Young, R. M. B.
Sommeria, J.
Didelle, H.
and
Viboud, S.
2015.
An experimental study of multiple zonal jet formation in rotating, thermally driven convective flows on a topographic beta-plane.
Physics of Fluids,
Vol. 27,
Issue. 8,
Hsu, Pei-Chun
Diamond, P. H.
and
Tobias, S. M.
2015.
Nonperturbative mean-field theory for minimum enstrophy relaxation.
Physical Review E,
Vol. 91,
Issue. 5,
Chen, Changheng
Kamenkovich, Igor
and
Berloff, Pavel
2015.
On the Dynamics of Flows Induced by Topographic Ridges.
Journal of Physical Oceanography,
Vol. 45,
Issue. 3,
p.
927.
Suhas, D. L.
and
Sukhatme, Jai
2015.
Low frequency modulation of jets in quasigeostrophic turbulence.
Physics of Fluids,
Vol. 27,
Issue. 1,
Williams, Paul D.
and
Kelsall, Christopher W.
2015.
The Dynamics of Baroclinic Zonal Jets*.
Journal of the Atmospheric Sciences,
Vol. 72,
Issue. 3,
p.
1137.
Hsu, Pei-Chun
and
Diamond, P. H.
2015.
On calculating the potential vorticity flux.
Physics of Plasmas,
Vol. 22,
Issue. 3,
Constantinou, Navid C.
Farrell, Brian F.
and
Ioannou, Petros J.
2016.
Statistical State Dynamics of Jet–Wave Coexistence in Barotropic Beta-Plane Turbulence.
Journal of the Atmospheric Sciences,
Vol. 73,
Issue. 5,
p.
2229.
Durston, Sam
and
Gilbert, Andrew D.
2016.
Transport and instability in driven two-dimensional magnetohydrodynamic flows.
Journal of Fluid Mechanics,
Vol. 799,
Issue. ,
p.
541.
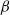 -plane is investigated using high-resolution, long-time numerical integrations, with particular emphasis on the late-time distribution of potential vorticity. The structure of the jets is found to depend in a simple way on a single non-dimensional parameter, which may be conveniently expressed as the ratio
-plane is investigated using high-resolution, long-time numerical integrations, with particular emphasis on the late-time distribution of potential vorticity. The structure of the jets is found to depend in a simple way on a single non-dimensional parameter, which may be conveniently expressed as the ratio 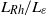 , where
, where  and
and 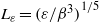 are two natural length scales arising in the problem; here
are two natural length scales arising in the problem; here 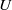 may be taken as the r.m.s. velocity,
may be taken as the r.m.s. velocity, 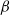 is the background gradient of potential vorticity in the north–south direction, and
is the background gradient of potential vorticity in the north–south direction, and  is the rate of energy input by the forcing. It is shown that jet strength increases with
is the rate of energy input by the forcing. It is shown that jet strength increases with 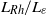 , with the limiting case of the potential vorticity staircase, comprising a monotonic, piecewise-constant profile in the north–south direction, being approached for
, with the limiting case of the potential vorticity staircase, comprising a monotonic, piecewise-constant profile in the north–south direction, being approached for 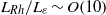 . At lower values, eddies created by the forcing become sufficiently intense to continually disrupt the steepening of potential vorticity gradients in the jet cores, preventing strong jets from developing. Although detailed features such as the regularity of jet spacing and intensity are found to depend on the spectral distribution of the forcing, the approach of the staircase limit with increasing
. At lower values, eddies created by the forcing become sufficiently intense to continually disrupt the steepening of potential vorticity gradients in the jet cores, preventing strong jets from developing. Although detailed features such as the regularity of jet spacing and intensity are found to depend on the spectral distribution of the forcing, the approach of the staircase limit with increasing 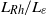 is robust across a variety of different forcing types considered.
is robust across a variety of different forcing types considered.
