Article contents
Surface thermodynamics and wetting condition in the multiphase lattice Boltzmann model with self-tuning equation of state
Published online by Cambridge University Press: 19 April 2022
Abstract
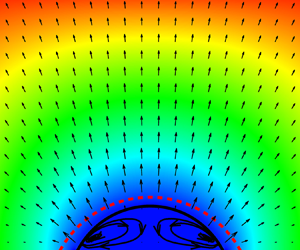
The surface thermodynamics and wetting condition are investigated for the recent multiphase lattice Boltzmann model with a self-tuning equation of state (EOS), where the multiphase EOS is specified in advance and the reduced temperature is set to a relatively low value. The surface thermodynamics is first explored starting from the free-energy functional of a multiphase system and a theoretical expression for the contact angle is derived for the general multiphase EOS. The conventional free-energy density for the solid surface, which is in linear form, is analysed, and it is found that the fluid density on the solid surface significantly deviates from that in the bulk phase when the reduced temperature is relatively low. A new free-energy density for the solid surface, which is in hyperbolic tangent form, is then proposed. Two independent parameters are introduced, which can dramatically reduce the density deviation and effectively adjust the contact angle, respectively. Meanwhile, the contact angle, surface tension and interface thickness can be independently adjusted in the present theoretical framework. Based on the analysed surface thermodynamics, a thermodynamically consistent treatment for the wetting condition is proposed for both straight and curved walls. Numerical tests of droplets on straight and curved walls validate the theoretical analysis of the surface thermodynamics and the present wetting condition treatment. As further applications, a moving droplet on an inclined wall, which is vertically and sinusoidally oscillated, and the evaporation of a droplet on an adiabatic substrate are simulated, and satisfying results consistent with previous studies are obtained.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 19
- Cited by


