Article contents
Transient perturbation growth in time-dependent mixing layers
Published online by Cambridge University Press: 01 February 2013
Abstract
We investigate numerically the transient linear growth of three-dimensional (3D) perturbations in a homogeneous time-evolving mixing layer in order to identify which perturbations are optimal in terms of their kinetic energy gain over a finite, predetermined time interval. We model the mixing layer with an initial parallel velocity distribution 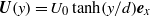 $\mathbi{U}(y)= {U}_{0} \tanh (y/ d)\mathbi{e}_{x}$ with Reynolds number
$\mathbi{U}(y)= {U}_{0} \tanh (y/ d)\mathbi{e}_{x}$ with Reynolds number 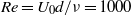 $Re= {U}_{0} d/ \nu = 1000$ , where
$Re= {U}_{0} d/ \nu = 1000$ , where  $\nu $ is the kinematic viscosity of the fluid. We consider a range of time intervals on both a constant ‘frozen’ base flow and a time-dependent two-dimensional (2D) flow associated with the growth and nonlinear saturation of two wavelengths of the most-unstable eigenmode of linear theory of the initial parallel velocity distribution, which rolls up into two classical Rayleigh instabilities commonly referred to as Kelvin–Helmholtz (KH) billows, which eventually pair to form a larger vortex. For short times, the most-amplified perturbations on the frozen
$\nu $ is the kinematic viscosity of the fluid. We consider a range of time intervals on both a constant ‘frozen’ base flow and a time-dependent two-dimensional (2D) flow associated with the growth and nonlinear saturation of two wavelengths of the most-unstable eigenmode of linear theory of the initial parallel velocity distribution, which rolls up into two classical Rayleigh instabilities commonly referred to as Kelvin–Helmholtz (KH) billows, which eventually pair to form a larger vortex. For short times, the most-amplified perturbations on the frozen 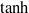 $\tanh $ profile are inherently 3D, and are most appropriately described as oblique wave ‘OL’ perturbations which grow through a combination of the Orr and lift-up mechanisms, while for longer times, the optimal perturbations are 2D and similar to the KH normal mode, with a slight enhancement of gain. For the time-evolving KH base flow, OL perturbations continue to dominate over sufficiently short time intervals. However, for longer time intervals which involve substantial evolution of the primary KH billows, two broad classes of inherently 3D linear optimal perturbation arise, associated at low wavenumbers with the well-known core-centred elliptical translative instability, and at higher wavenumbers with the braid-centred hyperbolic instability. The hyperbolic perturbation is relatively inefficient in exploiting the gain of the OL perturbations, and so only dominates the smaller wavenumber (ultimately) core-centred perturbations when the time evolution of the base flow or the start time of the optimization interval does not allow the OL perturbations much opportunity to grow. When the OL perturbations can grow, they initially grow in the braid, and then trigger an elliptical core-centred perturbation by a strong coupling with the primary KH billow. If the optimization time interval includes pairing of the primary billows, the secondary elliptical perturbations are strongly suppressed during the pairing event, due to the significant disruption of the primary billow cores during pairing.
$\tanh $ profile are inherently 3D, and are most appropriately described as oblique wave ‘OL’ perturbations which grow through a combination of the Orr and lift-up mechanisms, while for longer times, the optimal perturbations are 2D and similar to the KH normal mode, with a slight enhancement of gain. For the time-evolving KH base flow, OL perturbations continue to dominate over sufficiently short time intervals. However, for longer time intervals which involve substantial evolution of the primary KH billows, two broad classes of inherently 3D linear optimal perturbation arise, associated at low wavenumbers with the well-known core-centred elliptical translative instability, and at higher wavenumbers with the braid-centred hyperbolic instability. The hyperbolic perturbation is relatively inefficient in exploiting the gain of the OL perturbations, and so only dominates the smaller wavenumber (ultimately) core-centred perturbations when the time evolution of the base flow or the start time of the optimization interval does not allow the OL perturbations much opportunity to grow. When the OL perturbations can grow, they initially grow in the braid, and then trigger an elliptical core-centred perturbation by a strong coupling with the primary KH billow. If the optimization time interval includes pairing of the primary billows, the secondary elliptical perturbations are strongly suppressed during the pairing event, due to the significant disruption of the primary billow cores during pairing.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 49
- Cited by

