Article contents
Triglobal resolvent analysis of swept-wing wakes
Published online by Cambridge University Press: 09 January 2023
Abstract
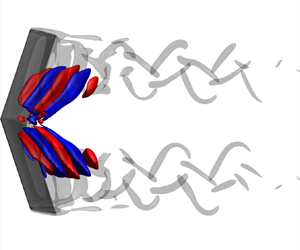
Through triglobal resolvent analysis, we reveal the effects of wing tip and sweep angle on laminar separated wakes over swept wings. For the present study, we consider wings with semi-aspect ratios from  $1$ to
$1$ to  $4$, sweep angles from
$4$, sweep angles from  $0^\circ$ to
$0^\circ$ to  $45^\circ$ and angles of attack of
$45^\circ$ and angles of attack of  $20^\circ$ and
$20^\circ$ and  $30^\circ$ at a chord-based Reynolds number of
$30^\circ$ at a chord-based Reynolds number of  $400$ and a Mach number of
$400$ and a Mach number of  $0.1$. Using direct numerical simulations, we observe that unswept wings develop vortex shedding near the wing root with a quasi-steady tip vortex. For swept wings, vortex shedding is seen near the wing tip for low sweep angles, while the wakes are steady for wings with high sweep angles. To gain further insights into the mechanisms of flow unsteadiness, triglobal resolvent analysis is used to identify the optimal spatial input–output mode pairs and the associated gains over a range of frequencies. The three-dimensional forcing and response modes reveal that harmonic fluctuations are directed towards the root for unswept wings and towards the wing tip for swept wings. The overlapping region of the forcing–response mode pairs uncovers triglobal resolvent wavemakers associated with self-sustained unsteady wakes of swept wings. Furthermore, we show that for low-aspect-ratio wings optimal perturbations develop globally over the entire wingspan. The present study uncovers physical insights on the effects of tip and sweep on the growth of optimal harmonic perturbations and the wake dynamics of separated flows over swept wings.
$0.1$. Using direct numerical simulations, we observe that unswept wings develop vortex shedding near the wing root with a quasi-steady tip vortex. For swept wings, vortex shedding is seen near the wing tip for low sweep angles, while the wakes are steady for wings with high sweep angles. To gain further insights into the mechanisms of flow unsteadiness, triglobal resolvent analysis is used to identify the optimal spatial input–output mode pairs and the associated gains over a range of frequencies. The three-dimensional forcing and response modes reveal that harmonic fluctuations are directed towards the root for unswept wings and towards the wing tip for swept wings. The overlapping region of the forcing–response mode pairs uncovers triglobal resolvent wavemakers associated with self-sustained unsteady wakes of swept wings. Furthermore, we show that for low-aspect-ratio wings optimal perturbations develop globally over the entire wingspan. The present study uncovers physical insights on the effects of tip and sweep on the growth of optimal harmonic perturbations and the wake dynamics of separated flows over swept wings.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 18
- Cited by


