Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Watanabe, Tomoaki
Sakai, Yasuhiko
Nagata, Kouji
Ito, Yasumasa
and
Hayase, Toshiyuki
2014.
Vortex stretching and compression near the turbulent/non-turbulent interface in a planar jet.
Journal of Fluid Mechanics,
Vol. 758,
Issue. ,
p.
754.
Philip, Jimmy
Meneveau, Charles
de Silva, Charitha M.
and
Marusic, Ivan
2014.
Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers.
Physics of Fluids,
Vol. 26,
Issue. 1,
Kwon, Y. S.
Philip, J.
de Silva, C. M.
Hutchins, N.
and
Monty, J. P.
2014.
The quiescent core of turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
228.
Chauhan, Kapil
Philip, Jimmy
and
Marusic, Ivan
2014.
Scaling of the turbulent/non-turbulent interface in boundary layers.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
298.
Vaghefi, Navid S.
and
Madnia, Cyrus K.
2015.
Local flow topology and velocity gradient invariants in compressible turbulent mixing layer.
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
67.
Watanabe, T.
Sakai, Y.
Nagata, K.
Ito, Y.
and
Hayase, T.
2015.
Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers.
Physics of Fluids,
Vol. 27,
Issue. 8,
Jahanbakhshi, R.
Vaghefi, N. S.
and
Madnia, C. K.
2015.
Baroclinic vorticity generation near the turbulent/ non-turbulent interface in a compressible shear layer.
Physics of Fluids,
Vol. 27,
Issue. 10,
Monkewitz, Peter A.
and
Nagib, Hassan M.
2015.
Large-Reynolds-number asymptotics of the streamwise normal stress in zero-pressure-gradient turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 783,
Issue. ,
p.
474.
Baars, W. J.
Talluru, K. M.
Hutchins, N.
and
Marusic, I.
2015.
Wavelet analysis of wall turbulence to study large-scale modulation of small scales.
Experiments in Fluids,
Vol. 56,
Issue. 10,
Eisma, Jerke
Westerweel, Jerry
Ooms, Gijs
and
Elsinga, Gerrit E.
2015.
Interfaces and internal layers in a turbulent boundary layer.
Physics of Fluids,
Vol. 27,
Issue. 5,
Hearst, R. Jason
Dogan, Eda
and
Ganapathisubramani, Bharathram
2016.
Proceedings of the 5th International Conference on Jets, Wakes and Separated Flows (ICJWSF2015).
Vol. 185,
Issue. ,
p.
325.
de Silva, Charitha M.
Hutchins, Nicholas
and
Marusic, Ivan
2016.
Uniform momentum zones in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
309.
Lozano-Durán, Adrián
and
Borrell, Guillem
2016.
Algorithm 964.
ACM Transactions on Mathematical Software,
Vol. 42,
Issue. 4,
p.
1.
Mistry, Dhiren
Philip, Jimmy
Dawson, James R.
and
Marusic, Ivan
2016.
Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
690.
Jahanbakhshi, Reza
and
Madnia, Cyrus K.
2016.
Entrainment in a compressible turbulent shear layer.
Journal of Fluid Mechanics,
Vol. 797,
Issue. ,
p.
564.
Borrell, Guillem
and
Jiménez, Javier
2016.
Properties of the turbulent/non-turbulent interface in boundary layers.
Journal of Fluid Mechanics,
Vol. 801,
Issue. ,
p.
554.
Rodríguez-López, Eduardo
Bruce, Paul J. K.
and
Buxton, Oliver R. H.
2016.
Near field development of artificially generated high Reynolds number turbulent boundary layers.
Physical Review Fluids,
Vol. 1,
Issue. 7,
Yang, Jongmin
Hwang, Jinyul
and
Sung, Hyung Jin
2016.
Structural organization of the quiescent core region in a turbulent channel flow.
International Journal of Heat and Fluid Flow,
Vol. 62,
Issue. ,
p.
455.
Squire, D. T.
Morrill-Winter, C.
Hutchins, N.
Marusic, I.
Schultz, M. P.
and
Klewicki, J. C.
2016.
Smooth- and rough-wall boundary layer structure from high spatial range particle image velocimetry.
Physical Review Fluids,
Vol. 1,
Issue. 6,
Kwon, Y. S.
Hutchins, N.
and
Monty, J. P.
2016.
On the use of the Reynolds decomposition in the intermittent region of turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
p.
5.
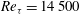 $\mathit{Re}_\tau =14\, 500$ ) is examined using particle image velocimetry. An experimental set-up is utilized that employs multiple high-resolution cameras to capture a large field of view that extends
$\mathit{Re}_\tau =14\, 500$ ) is examined using particle image velocimetry. An experimental set-up is utilized that employs multiple high-resolution cameras to capture a large field of view that extends 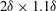 $2\delta \times 1.1\delta $ in the streamwise/wall-normal plane with an unprecedented dynamic range. The interface is detected using a criteria of local turbulent kinetic energy and proves to be an effective method for boundary layers. The presence of a turbulent/non-turbulent superlayer is corroborated by the presence of a jump for the conditionally averaged streamwise velocity across the interface. The steep change in velocity is accompanied by a discontinuity in vorticity and a sharp rise in the Reynolds shear stress. The conditional statistics at the interface are in quantitative agreement with the superlayer equations outlined by Reynolds (J. Fluid Mech., vol. 54, 1972, pp. 481–488). Further analysis introduces the mass flux as a physically relevant parameter that provides a direct quantitative insight into the entrainment. Consistency of this approach is first established via the equality of mean entrainment calculations obtained using three different methods, namely, conditional, instantaneous and mean equations of motion. By means of ‘mass-flux spectra’ it is shown that the boundary-layer entrainment is characterized by two distinctive length scales which appear to be associated with a two-stage entrainment process and have a substantial scale separation.
$2\delta \times 1.1\delta $ in the streamwise/wall-normal plane with an unprecedented dynamic range. The interface is detected using a criteria of local turbulent kinetic energy and proves to be an effective method for boundary layers. The presence of a turbulent/non-turbulent superlayer is corroborated by the presence of a jump for the conditionally averaged streamwise velocity across the interface. The steep change in velocity is accompanied by a discontinuity in vorticity and a sharp rise in the Reynolds shear stress. The conditional statistics at the interface are in quantitative agreement with the superlayer equations outlined by Reynolds (J. Fluid Mech., vol. 54, 1972, pp. 481–488). Further analysis introduces the mass flux as a physically relevant parameter that provides a direct quantitative insight into the entrainment. Consistency of this approach is first established via the equality of mean entrainment calculations obtained using three different methods, namely, conditional, instantaneous and mean equations of motion. By means of ‘mass-flux spectra’ it is shown that the boundary-layer entrainment is characterized by two distinctive length scales which appear to be associated with a two-stage entrainment process and have a substantial scale separation.
