Hostname: page-component-5b777bbd6c-vfh8q Total loading time: 0 Render date: 2025-06-25T11:11:15.690Z Has data issue: false hasContentIssue false
  • English
  • Français

Vibration-induced morphological evolution of a melting solid under microgravity

Published online by Cambridge University Press:  16 December 2024

Wen-Ping Fang ,
Jian-Zhao Wu Open the ORCID record for Jian-Zhao Wu [Opens in a new window] ,
Ze-Lin Huang ,
Bo-Fu Wang Open the ORCID record for Bo-Fu Wang [Opens in a new window] ,
Quan Zhou Open the ORCID record for Quan Zhou [Opens in a new window]  and
Kai Leong Chong Open the ORCID record for Kai Leong Chong [Opens in a new window]
Wen-Ping Fang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Jian-Zhao Wu
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China Shanghai Institute of Aircraft Mechanics and Control, Zhangwu Road, Shanghai 200092, PR China
Ze-Lin Huang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Bo-Fu Wang
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Quan Zhou
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China
Kai Leong Chong*
Affiliation:
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai Institute of Applied Mathematics and Mechanics, School of Mechanics and Engineering Science, Shanghai University, Shanghai 200072, PR China Shanghai Institute of Aircraft Mechanics and Control, Zhangwu Road, Shanghai 200092, PR China
*
†Email address for correspondence: klchong@shu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

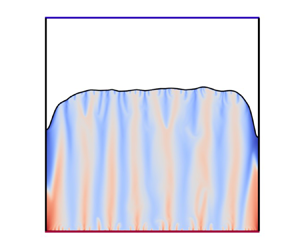
We study the melting process of a solid under microgravity, driven solely by lateral vibrations that are perpendicular to the applied temperature gradient due to the absence of gravity-induced convection. Using direct numerical simulations with the phase-field method, we examine two-dimensional vibration-induced melting in a square cavity over four orders of magnitude of vibrational Rayleigh numbers, $10^5\le Ra_{{vib}}\le 10^9$. Our results show that as melting progresses, the flow structure transitions from a periodic-circulation regime with diffusion-dominated heat transfer to a columnar regime with vibroconvection. The mean height of the liquid–solid interface follows a power-law dependency with time, $\bar {\xi } \sim \tilde t^{1/(2-2\alpha )}$, where $\alpha = 0$ in the periodic-circulation regime and $\alpha = 1/2$ in the columnar regime. We further observe that within the columnar regime, the morphological evolution of the liquid–solid interface is influenced by the interaction of columnar thermal plumes in the central regions and the peripheral flow near the sidewalls. Specifically, we offer a comprehensive analysis of the plume merging behaviour, which is governed by the aspect ratio ($\bar {\xi }$) of the liquid layer and the intensity of vibration, quantified by the effective vibrational Rayleigh number $Ra_{vib}^{eff}$. We identify the relationship between the number of columnar plumes $K_m$ and $Ra_{vib}^{eff}$, finding that $K_m \sim \bar {\xi }^{-1} (Ra_{vib}^{eff})^{\gamma }$ with the fitting scaling exponent $\gamma = 0.150 \pm 0.025$. We subsequently quantify the characteristics of the interface roughness amplitude evolution in microgravity vibroconvection. Our results indicate that the roughness amplitude exhibits a power-law dependence on the mean height of the liquid layer. Drawing from the Stefan boundary condition, we theoretically deduce this dependence under the assumption of a non-uniform heat flux distribution at the interface, where the theory is corroborated by our numerical simulations.

JFM classification

Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A43
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

‡

These authors contributed equally to this work.

References

Bannister, T., Grodzka, P., Spradley, L., Bourgeois, S., Jr., Hedden, R. & Facemire, B. 1973 Apollo 17 heat flow and convection experiments: final data analyses results. NASA TM X–64772.Google Scholar
Beysens, D. 2006 Vibrations in space as an artificial gravity? Europhys. News 37 (3), 22–25.CrossRefGoogle Scholar
Braibanti, M., et al. 2019 European space agency experiments on thermodiffusion of fluid mixtures in space. Eur. Phys. J. E 42, 1–11.CrossRefGoogle ScholarPubMed
Bushuk, M., Holland, D.M., Stanton, T.P., Stern, A. & Gray, C. 2019 Ice scallops: a laboratory investigation of the ice–water interface. J. Fluid Mech. 873, 942–976.CrossRefGoogle ScholarPubMed
Carbo, R.M., Smith, R.W. & Poese, M.E. 2014 A computational model for the dynamic stabilization of Rayleigh–Bénard convection in a cubic cavity. J. Acoust. Soc. Am. 135 (2), 654–668.CrossRefGoogle Scholar
Chen, X., Hao, G., Yao, F. & Zhang, C. 2019 Numerical study on melting phase change under microgravity. Microgravity Sci. Technol. 31, 793–803.CrossRefGoogle Scholar
Chong, K.L., Qiao, S., Wu, J.-Z. & Wang, B.-F. 2024 Heat transfer enhancement in vertical convection under spatially harmonic temperature modulation. Intl J. Heat Mass Transfer 227, 125452.CrossRefGoogle Scholar
Cissé, I., Bardan, G. & Mojtabi, A. 2004 Rayleigh–Bénard convective instability of a fluid under high-frequency vibration. Intl J. Heat Mass Transfer 47 (19-20), 4101–4112.CrossRefGoogle Scholar
Couston, L.-A., Hester, E., Favier, B., Taylor, J.R., Holland, P.R. & Jenkins, A. 2021 Topography generation by melting and freezing in a turbulent shear flow. J. Fluid Mech. 911, A44.CrossRefGoogle Scholar
Davis, S.H., Müller, U. & Dietsche, C. 1984 Pattern selection in single-component systems coupling Bénard convection and solidification. J. Fluid Mech. 144, 133–151.CrossRefGoogle Scholar
Demin, V., Gershuni, G. & Verkholantsev, I. 1996 Mechanical quasi-equilibrium and thermovibrational convective instability in an inclined fluid layer. Intl J. Heat Mass Transfer 39 (9), 1979–1991.CrossRefGoogle Scholar
Dhaidan, N.S., Khodadadi, J., Al-Hattab, T.A. & Al-Mashat, S.M. 2013 Experimental and numerical investigation of melting of NePCM inside an annular container under a constant heat flux including the effect of eccentricity. Intl J. Heat Mass Transfer 67, 455–468.CrossRefGoogle Scholar
Du, Y., Wang, Z., Jiang, L., Calzavarini, E. & Sun, C. 2023 Sea water freezing modes in a natural convection system. J. Fluid Mech. 960, A35.CrossRefGoogle Scholar
Favier, B., Purseed, J. & Duchemin, L. 2019 Rayleigh–Bénard convection with a melting boundary. J. Fluid Mech. 858, 437–473.CrossRefGoogle Scholar
FitzMaurice, A., Cenedese, C. & Straneo, F. 2017 Nonlinear response of iceberg side melting to ocean currents. Geophys. Res. Lett. 44 (11), 5637–5644.CrossRefGoogle Scholar
Garrabos, Y., Beysens, D., Lecoutre, C., Dejoan, A., Polezhaev, V. & Emelianov, V. 2007 Thermoconvectional phenomena induced by vibrations in supercritical S F 6 under weightlessness. Phys. Rev. E 75 (5), 056317.CrossRefGoogle Scholar
Gershuni, G.Z. & Lyubimov, D.V. 1998 Thermal Vibrational Convection. Wiley & Sons.Google Scholar
Glicksman, M., Lupulescu, A. & Koss, M. 2003 Melting in microgravity. J. Thermophys. Heat Transfer 17 (1), 69–76.CrossRefGoogle Scholar
Grodzka, P.G. & Bannister, T.C. 1975 Heat flow and convection experiments aboard apollo 17. Science 187 (4172), 165–167.CrossRefGoogle ScholarPubMed
Guo, C., Qu, T., Yu, Y. & Zhou, J. 2024 a Effects of mechanical vibration on melting characteristics of latent thermal energy storage units using the dynamic mesh method. Appl. Therm. Engng 252, 123678.CrossRefGoogle Scholar
Guo, X., Qin, P., Wu, J., Wang, B., Chong, K.L. & Zhou, Q. 2024 b Statistics of kinetic and thermal energy dissipation rates in two-dimensional thermal vibrational convection. Phys. Fluids 36 (7), 075132.Google Scholar
Guo, X.-L., Wu, J.-Z., Wang, B.-F., Zhou, Q. & Chong, K.L. 2023 Flow structure transition in thermal vibrational convection. J. Fluid Mech. 974, A29.CrossRefGoogle Scholar
Guo, X.-Q., Wang, B.-F., Wu, J.-Z., Chong, K.L. & Zhou, Q. 2022 Turbulent vertical convection under vertical vibration. Phys. Fluids 34 (5), 055106.Google Scholar
Hester, E.W., Couston, L. -A., Favier, B., Burns, K.J. & Vasil, G.M. 2020 Improved phase-field models of melting and dissolution in multi-component flows. Proc. R. Soc. A 476 (2242), 20200508.CrossRefGoogle ScholarPubMed
Hester, E.W., McConnochie, C.D., Cenedese, C., Couston, L.-A. & Vasil, G. 2021 Aspect ratio affects iceberg melting. Phys. Rev. Fluids 6 (2), 023802.CrossRefGoogle Scholar
Hock, R. 2005 Glacier melt: a review of processes and their modelling. Prog. Phys. Geog. 29 (3), 362–391.CrossRefGoogle Scholar
Hosseinizadeh, S., Darzi, A.R. & Tan, F. 2012 Numerical investigations of unconstrained melting of nano-enhanced phase change material (NEPCM) inside a spherical container. Intl J. Therm. Sci. 51, 77–83.CrossRefGoogle Scholar
Huang, Z.-L., Guo, X.-L., Wu, J.-Z., Wang, B.-F., Chong, K.L. & Zhou, Q. 2023 Rayleigh-number dependence of the critical vibration frequency in vibrating thermal turbulence. Phys. Rev. Fluids 8 (11), 113501.CrossRefGoogle Scholar
Huang, Z.-L., Wu, J.-Z., Guo, X.-L., Zhao, C.-B., Wang, B.-F., Chong, K.L. & Zhou, Q. 2024 Unifying constitutive law of vibroconvective turbulence in microgravity. J. Fluid Mech. 987, A14.CrossRefGoogle Scholar
Kamkari, B. & Amlashi, H.J. 2017 Numerical simulation and experimental verification of constrained melting of phase change material in inclined rectangular enclosures. Intl Commun. Heat Mass Transfer 88, 211–219.CrossRefGoogle Scholar
Li, X., Ma, T., Liu, J., Liu, L. & Wang, Q. 2017 Investigation of gravity effect on phase change heat transfer using the Lattice Boltzmann method. Energy Procedia 142, 3902–3907.CrossRefGoogle Scholar
Mahmud, H. & Ahmed, D.H. 2022 Numerical investigations on melting of phase change material (PCM) with different arrangements of heat source-sink pairs under microgravity. Microgravity Sci. Technol. 34 (2), 20.CrossRefGoogle Scholar
Meng, W.-S., Zhao, C.-B., Wu, J.-Z., Wang, B.-F., Zhou, Q. & Chong, K.L. 2024 Simulation of flow and debris migration in extreme ultraviolet source vessel. Phys. Fluids 36 (2), 023322.CrossRefGoogle Scholar
Mialdun, A., Ryzhkov, I., Melnikov, D. & Shevtsova, V. 2008 Experimental evidence of thermal vibrational convection in a nonuniformly heated fluid in a reduced gravity environment. Phys. Rev. Lett. 101 (8), 084501.CrossRefGoogle Scholar
Porter, J., Sánchez, P.S., Shevtsova, V. & Yasnou, V. 2021 A review of fluid instabilities and control strategies with applications in microgravity. Math. Model. Nat. Pheno. 16, 24.CrossRefGoogle Scholar
Purseed, J., Favier, B., Duchemin, L. & Hester, E.W. 2020 Bistability in Rayleigh–Bénard convection with a melting boundary. Phys. Rev. Fluids 5 (2), 023501.CrossRefGoogle Scholar
Rahmanian, S., Rahmanian-Koushkaki, H., Moein-Jahromi, M. & Saidur, R. 2023 A novel method to improve the performance of pcm thermal energy storage units using a small oscillator plate-numerical analysis. J. Energy Storage 73, 108900.CrossRefGoogle Scholar
Raoux, S. 2009 Phase change materials. Annu. Rev. Mater. Res. 39, 25–48.CrossRefGoogle Scholar
Ravichandran, S. & Wettlaufer, J.S. 2021 Melting driven by rotating Rayleigh–Bénard convection. J. Fluid Mech. 916, A28.CrossRefGoogle Scholar
Sánchez, P.S., Ezquerro, J., Fernandez, J. & Rodriguez, J. 2020 a Thermocapillary effects during the melting of phase change materials in microgravity: heat transport enhancement. Intl J. Heat Mass Transfer 163, 120478.CrossRefGoogle Scholar
Sánchez, P.S., Ezquerro, J., Fernandez, J. & Rodriguez, J. 2021 Thermocapillary effects during the melting of phase-change materials in microgravity: steady and oscillatory flow regimes. J. Fluid Mech. 908, A20.CrossRefGoogle Scholar
Sánchez, P.S., Gaponenko, Y., Yasnou, V., Mialdun, A., Porter, J. & Shevtsova, V. 2020 b Effect of initial interface orientation on patterns produced by vibrational forcing in microgravity. J. Fluid Mech. 884, A38.CrossRefGoogle Scholar
Sánchez, P.S., Yasnou, V., Gaponenko, Y., Mialdun, A., Porter, J. & Shevtsova, V. 2019 Interfacial phenomena in immiscible liquids subjected to vibrations in microgravity. J. Fluid Mech. 865, 850–883.CrossRefGoogle Scholar
Šeta, B., Dubert, D., Gavalda, J., Massons, J., Bou-Ali, M.M., Ruiz, X. & Shevtsova, V. 2023 Effect of heat transfer through an interface on convective melting dynamics of phase change materials. J. Fluid Mech. 966, A46.CrossRefGoogle Scholar
Shevtsova, V., Ryzhkov, I.I., Melnikov, D.E., Gaponenko, Y.A. & Mialdun, A. 2010 Experimental and theoretical study of vibration-induced thermal convection in low gravity. J. Fluid Mech. 648, 53–82.CrossRefGoogle Scholar
Thomas, S.K., Cassoni, R.P. & MacArthur, C.D. 1996 Aircraft anti-icing and de-icing techniques and modeling. J. Aircraft 33 (5), 841–854.CrossRefGoogle Scholar
Ulvrová, M., Labrosse, S., Coltice, N., Råback, P. & Tackley, P. 2012 Numerical modelling of convection interacting with a melting and solidification front: application to the thermal evolution of the basal magma ocean. Phys. Earth Planet. Inter. 206, 51–66.CrossRefGoogle Scholar
Wang, B.-F., Zhou, Q. & Sun, C. 2020 Vibration-induced boundary-layer destabilization achieves massive heat-transport enhancement. Sci. Adv. 6 (21), eaaz8239.CrossRefGoogle ScholarPubMed
Wang, Z., Calzavarini, E., Sun, C. & Toschi, F. 2021 How the growth of ice depends on the fluid dynamics underneath. Proc. Natl Acad. Sci. USA 118 (10), e2012870118.CrossRefGoogle ScholarPubMed
Wilson, N.J., Vreugdenhil, C.A., Gayen, B. & Hester, E.W. 2023 Double-diffusive layer and meltwater plume effects on ice face scalloping in phase-change simulations. Geophys. Res. Lett. 50 (17), e2023GL104396.CrossRefGoogle Scholar
Wu, J.-Z., Dong, Y.-H., Wang, B.-F. & Zhou, Q. 2021 Phase decomposition analysis on oscillatory Rayleigh–Bénard turbulence. Phys. Fluids 33 (4), 045108.CrossRefGoogle Scholar
Wu, J.-Z., Wang, B.-F., Chong, K.L., Dong, Y.-H., Sun, C. & Zhou, Q. 2022 a Vibration-induced ‘anti-gravity’ tames thermal turbulence at high Rayleigh numbers. J. Fluid Mech. 951, A13.CrossRefGoogle Scholar
Wu, J.-Z., Wang, B.-F. & Zhou, Q. 2022 b Massive heat transfer enhancement of Rayleigh–Bénard turbulence over rough surfaces and under horizontal vibration. Acta Mechanica Sin. 38 (2), 321319.CrossRefGoogle Scholar
Yang, R., Chong, K.L., Liu, H.-R., Verzicco, R. & Lohse, D. 2022 Abrupt transition from slow to fast melting of ice. Phys. Rev. Fluids 7 (8), 083503.CrossRefGoogle Scholar
Yang, R., Howland, C.J., Liu, H.-R., Verzicco, R. & Lohse, D. 2023 a Ice melting in salty water: layering and non-monotonic dependence on the mean salinity. J. Fluid Mech. 969, R2.CrossRefGoogle Scholar
Yang, R., Howland, C.J., Liu, H.-R., Verzicco, R. & Lohse, D. 2023 b Morphology evolution of a melting solid layer above its melt heated from below. J. Fluid Mech. 956, A23.CrossRefGoogle Scholar
Yang, R., Howland, C.J., Liu, H.-R., Verzicco, R. & Lohse, D. 2024 Shape effect on solid melting in flowing liquid. J. Fluid Mech. 980, R1.CrossRefGoogle Scholar
Zhang, Y. & Zhou, Q. 2024 Low-Prandtl-number effects on global and local statistics in two-dimensional Rayleigh–Bénard convection. Phys. Fluids 36 (1), 015107.CrossRefGoogle Scholar
Zhao, C.-B., Wang, B.-F., Wu, J.-Z., Chong, K.L. & Zhou, Q. 2022 a Suppression of flow reversals via manipulating corner rolls in plane Rayleigh–Bénard convection. J. Fluid Mech. 946, A44.CrossRefGoogle Scholar
Zhao, C.-B., Wu, J.-Z., Wang, B.-F., Chang, T., Zhou, Q. & Chong, K.L. 2024 Numerical study on the onset of global-scale flow from individual buoyant plumes: implications for indoor disease transmission. Phys. Fluids 36 (3), 035149.CrossRefGoogle Scholar
Zhao, C.-B., Zhang, Y.-Z., Wang, B.-F., Wu, J.-Z., Chong, K.L. & Zhou, Q. 2022 b Modulation of turbulent Rayleigh–Bénard convection under spatially harmonic heating. Phys. Rev. E 105 (5), 055107.CrossRefGoogle ScholarPubMed