Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T18:54:34.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall-to-wall optimal transport in two dimensions

Published online by Cambridge University Press:  28 February 2020

Andre N. Souza Open the ORCID record for Andre N. Souza [Opens in a new window] ,
Ian Tobasco  and
Charles R. Doering
Andre N. Souza*
Affiliation:
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Ian Tobasco
Affiliation:
Department of Mathematics, Statistics, and Computer Science, University of Illinois at Chicago, 851 S. Morgan Street, Chicago, IL 60607-7045, USA
Charles R. Doering
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109-1043, USA Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109-1042, USA Department of Physics, University of Michigan, Ann Arbor, MI 48109-1140, USA
*
†Email address for correspondence: andrenogueirasouza@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

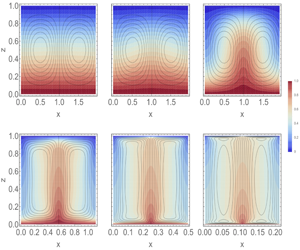
Gradient ascent methods are developed to compute incompressible flows that maximize heat transport between two isothermal no-slip parallel walls. Parameterizing the magnitude of the velocity fields by a Péclet number $Pe$ proportional to their root-mean-square rate of strain, the schemes are applied to compute two-dimensional flows optimizing convective enhancement of diffusive heat transfer, i.e. the Nusselt number $Nu$ up to $Pe\approx 10^{5}$. The resulting transport exhibits a change of scaling from $Nu-1\sim Pe^{2}$ for $Pe<10$ in the linear regime to $Nu\sim Pe^{0.54}$ for $Pe>10^{3}$. Optimal fields are observed to be approximately separable, i.e. products of functions of the wall-parallel and wall-normal coordinates. Analysis employing a separable ansatz yields a conditional upper bound ${\lesssim}Pe^{6/11}=Pe^{0.\overline{54}}$ as $Pe\rightarrow \infty$ similar to the computationally achieved scaling. Implications for heat transfer in buoyancy-driven Rayleigh–Bénard convection are discussed.

JFM classification

Mathematical Foundations: Variational methods Flow Control: Mixing enhancement
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A34
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2017 Improved convection cooling in steady channel flows. Phys. Rev. Fluids 2, 104501.CrossRefGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Busse, F. H. 1969 On Howard’s bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.CrossRefGoogle Scholar
Ding, Z. & Kerswell, R. R.2019 Exhausting the background approach for bounding the heat transport in Rayleigh–Bénard convection. J. Fluid Mech. (submitted).Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53, 5957–5981.Google ScholarPubMed
Doering, C. R. & Tobasco, I. 2019 On the optimal design of wall-to-wall heat transport. Commun. Pure Appl. Maths 72, 2385–2448.CrossRefGoogle Scholar
Feynman, R. P. & Hibbs, A. R. 1965 Quantum Mechanics and Path Integrals, 1st edn. McGraw-Hill.Google Scholar
Hassanzadeh, P., Chini, G. P. & Doering, C. R. 2014 Wall to wall optimal transport. J. Fluid Mech. 751, 627–662.CrossRefGoogle Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.CrossRefGoogle Scholar
Kerswell, R. R. 1998 Unification of variational principles for turbulent shear flows: the background method of Doering-Constantin and the mean-fluctuation formulation of Howard-Busse. Physica D 121, 175–192.Google Scholar
Kleiser, L. & Schumann, U. 1980 Treatment of incompressibility and boundary conditions in 3-D numerical spectral simulations of plane channel flows. In Proceedings of the 3rd Conference on Numerical Methods in Fluid Mechanics (ed. Hirschel, E. H.), pp. 165–173. Springer.CrossRefGoogle Scholar
Malkus, W. V. R. 1954 Discrete transitions in turbulent convection. Proc. R. Soc. Lond. 225, 185–195.Google Scholar
Marcotte, F., Doering, C. R., Thiffeault, J.-L. & Young, W. R. 2018 Optimal heat transfer and optimal exit times. SIAM J. Appl. Maths 78 (1), 591–608.CrossRefGoogle Scholar
Motoki, S., Kawahara, G. & Shimizu, M. 2018a Maximal heat transfer between two parallel plates. J. Fluid Mech. 851, R4.CrossRefGoogle Scholar
Motoki, S., Kawahara, G. & Shimizu, M. 2018b Optimal heat transfer enhancement in plane Couette flow. J. Fluid Mech. 835, 1157–1198.CrossRefGoogle Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.CrossRefGoogle Scholar
Souza, A. N.2016 An optimal control approach to bounding transport properties of thermal convection. Doctoral thesis, University of Michigan.Google Scholar
Souza, A. N. & Doering, C. R. 2015a Maximal transport in the Lorenz equations. Phys. Lett. A 379, 518–523.CrossRefGoogle Scholar
Souza, A. N. & Doering, C. R. 2015b Transport bounds for a truncated model of Rayleigh–Bénard convection. Physica D 308, 26–33.CrossRefGoogle Scholar
Tobasco, I. & Doering, C. R. 2017 Optimal wall-to-wall transport by incompressible flows. Phys. Rev. Lett. 118, 264502.CrossRefGoogle ScholarPubMed
Toppaladoddi, S., Succi, S. & Wettlaufer, J. S. 2017 Roughness as a route to the ultimate regime of thermal convection. Phys. Rev. Lett. 118, 074503.CrossRefGoogle ScholarPubMed
Trefethen, L. N. 2001 Spectral Methods in MATLAB, 1st edn. SIAM.Google Scholar
Viswanath, D. 2015 Spectral integration of linear boundary value problems. J. Comput. Appl. Maths 290, 159–173.CrossRefGoogle Scholar
Viswanath, D. & Tobasco, I. 2013 Navier–Stokes solver using Green’s functions I: channel flow and plane Couette flow. J. Comput. Phys. 251, 414–431.CrossRefGoogle Scholar
Wen, B., Chini, G. P., Kerswell, R. R. & Doering, C. R. 2015 Time-stepping approach for solving upper-bound problems: Application to two-dimensional Rayleigh-Bénard convection. Phys. Rev. E 92 (4), 043012.CrossRefGoogle ScholarPubMed