Published online by Cambridge University Press: 04 March 2014
We report results from an experimental study of cavity formation during the impact of superhydrophobic spheres onto water. Using a simple splash-guard mechanism, we block the spray emerging during initial contact from closing thus eliminating the phenomenon known as ‘surface seal’, which typically occurs at Froude numbers 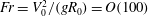 $\mathit{Fr}= V_{0}^{2}/(gR_{0}) = O(100)$ . As such, we are able to observe the evolution of a smooth cavity in a more extended parameter space than has been achieved in previous studies. Furthermore, by systematically varying the tank size and sphere diameter, we examine the influence of increasing wall effects on these guarded impact cavities and note the formation of surface undulations with wavelength
$\mathit{Fr}= V_{0}^{2}/(gR_{0}) = O(100)$ . As such, we are able to observe the evolution of a smooth cavity in a more extended parameter space than has been achieved in previous studies. Furthermore, by systematically varying the tank size and sphere diameter, we examine the influence of increasing wall effects on these guarded impact cavities and note the formation of surface undulations with wavelength 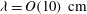 $\lambda =O(10)~ \mathrm{cm}$ and acoustic waves
$\lambda =O(10)~ \mathrm{cm}$ and acoustic waves 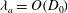 $\lambda _{a}=O(D_{0})$ along the cavity interface, which produce multiple pinch-off points. Acoustic waves are initiated by pressure perturbations, which themselves are generated by the primary cavity pinch-off. Using high-speed particle image velocimetry (PIV) techniques we study the bulk fluid flow for the most constrained geometry and show the larger undulations (
$\lambda _{a}=O(D_{0})$ along the cavity interface, which produce multiple pinch-off points. Acoustic waves are initiated by pressure perturbations, which themselves are generated by the primary cavity pinch-off. Using high-speed particle image velocimetry (PIV) techniques we study the bulk fluid flow for the most constrained geometry and show the larger undulations ( 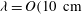 $\lambda =O (10~ \mathrm{cm}$ )) have a fixed nature with respect to the lab frame. We show that previously deduced scalings for the normalized (primary) pinch-off location (ratio of pinch-off depth to sphere depth at pinch-off time),
$\lambda =O (10~ \mathrm{cm}$ )) have a fixed nature with respect to the lab frame. We show that previously deduced scalings for the normalized (primary) pinch-off location (ratio of pinch-off depth to sphere depth at pinch-off time), 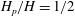 $H_{p}/H = 1/2$ , and pinch-off time,
$H_{p}/H = 1/2$ , and pinch-off time, 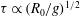 $\tau \propto (R_{0}/g)^{1/2}$ , do not hold for these extended cavities in the presence of strong wall effects (sphere-to-tank diameter ratio),
$\tau \propto (R_{0}/g)^{1/2}$ , do not hold for these extended cavities in the presence of strong wall effects (sphere-to-tank diameter ratio), 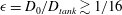 $\epsilon = D_{0}/D_{tank} \gtrsim 1/16$ . Instead, we find multiple distinct regimes for values of
$\epsilon = D_{0}/D_{tank} \gtrsim 1/16$ . Instead, we find multiple distinct regimes for values of 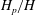 $H_{p}/H$ as the observed undulations are induced above the first pinch-off point as the impact speed increases. We also report observations of ‘kinked’ pinch-off points and the suppression of downward facing jets in the presence of wall effects. Surprisingly, upward facing jets emanating from first cavity pinch-off points evolve into a ‘flat’ structure at high impact speeds, both in the presence and absence of wall effects.
$H_{p}/H$ as the observed undulations are induced above the first pinch-off point as the impact speed increases. We also report observations of ‘kinked’ pinch-off points and the suppression of downward facing jets in the presence of wall effects. Surprisingly, upward facing jets emanating from first cavity pinch-off points evolve into a ‘flat’ structure at high impact speeds, both in the presence and absence of wall effects.
Comparison of “free” and “guarded” impact cavities formed during the impact of a 20 mm diameter sphere onto water at 8.4 m/s. The left panel is for free impact, where surface seal occurs, whilst the right panel shows the guarded impact, where surface seal is inhibited. Fr = 720, We = 9800, ε = 0.04, Bo = 13.6, Cn = 2.8. Original frame rate used was 10000 fps, playback speed is 30 fps showing only every 10th frame.
Comparison of “guarded” impact cavities formed during the impact of a 15 mm diameter sphere onto water under severe wall effects using a 8 cm square tank for various impact speeds of 2.8, 4.4, 6.4 and 8.4 m/s. Fr = 107 - 959, ε = 0.19, Bo = 7.6. Original frame rate used was 10000 fps, playback speed is 30 fps showing only every other frame.
Close-up view of the cavity pinch-off after the impact of a 20 mm diameter sphere onto water at 8.4 m/s under moderate wall effects using a 20 cm square tank. Fr = 720, ε = 0.1, Bo = 13.6. Original frame rate used was 10000 fps, playback speed is 30 fps showing only every 4th frame.