Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Naso, Aurore
and
Godeferd, Fabien S
2012.
Statistics of the perceived velocity gradient tensor in a rotating turbulent flow.
New Journal of Physics,
Vol. 14,
Issue. 12,
p.
125002.
Bellani, G
and
Variano, E A
2012.
Slip velocity of large neutrally buoyant particles in turbulent flows.
New Journal of Physics,
Vol. 14,
Issue. 12,
p.
125009.
Guseva, Ksenia
Feudel, Ulrike
and
Tél, Tamás
2013.
Influence of the history force on inertial particle advection: Gravitational effects and horizontal diffusion.
Physical Review E,
Vol. 88,
Issue. 4,
Krekhov, Alexei
Weith, Vanessa
and
Zimmermann, Walter
2013.
Periodic structures in binary mixtures enforced by Janus particles.
Physical Review E,
Vol. 88,
Issue. 4,
Klein, Simon
Gibert, Mathieu
Bérut, Antoine
and
Bodenschatz, Eberhard
2013.
Simultaneous 3D measurement of the translation and rotation of finite-size particles and the flow field in a fully developed turbulent water flow.
Measurement Science and Technology,
Vol. 24,
Issue. 2,
p.
024006.
Ray, Baidurja
and
Collins, Lance R.
2013.
Investigation of sub-Kolmogorov inertial particle pair dynamics in turbulence using novel satellite particle simulations.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
192.
Ray, Baidurja
and
Collins, Lance R.
2014.
A subgrid model for clustering of high-inertia particles in large-eddy simulations of turbulence.
Journal of Turbulence,
Vol. 15,
Issue. 6,
p.
366.
Voßkuhle, Michel
Pumir, Alain
Lévêque, Emmanuel
and
Wilkinson, Michael
2014.
Prevalence of the sling effect for enhancing collision rates in turbulent suspensions.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
841.
Gustavsson, K.
Vajedi, S.
and
Mehlig, B.
2014.
Clustering of Particles Falling in a Turbulent Flow.
Physical Review Letters,
Vol. 112,
Issue. 21,
Ravichandran, S.
Perlekar, Prasad
and
Govindarajan, Rama
2014.
Attracting fixed points for heavy particles in the vicinity of a vortex pair.
Physics of Fluids,
Vol. 26,
Issue. 1,
Siebert, H.
Shaw, R. A.
Ditas, J.
Schmeissner, T.
Malinowski, S. P.
Bodenschatz, E.
and
Xu, H.
2015.
High-resolution measurement of cloud microphysics and turbulence at a mountaintop station.
Atmospheric Measurement Techniques,
Vol. 8,
Issue. 8,
p.
3219.
Ravichandran, S.
and
Govindarajan, Rama
2015.
Caustics and clustering in the vicinity of a vortex.
Physics of Fluids,
Vol. 27,
Issue. 3,
Michalec, François-Gaël
Souissi, Sami
and
Holzner, Markus
2015.
Turbulence triggers vigorous swimming but hinders motion strategy in planktonic copepods.
Journal of The Royal Society Interface,
Vol. 12,
Issue. 106,
p.
20150158.
Vajedi, S.
Gustavsson, K.
Mehlig, B.
and
Biferale, L.
2016.
Inertial-particle accelerations in turbulence: a Lagrangian closure.
Journal of Fluid Mechanics,
Vol. 798,
Issue. ,
p.
187.
Frankel, Ari
Pouransari, H.
Coletti, F.
and
Mani, A.
2016.
Settling of heated particles in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 792,
Issue. ,
p.
869.
Wang, Steven
Stewart, Robert L
and
Metcalfe, Guy
2016.
Visualization of the trapping of inertial particles in a laminar mixing tank.
Chemical Engineering Science,
Vol. 143,
Issue. ,
p.
99.
Gustavsson, K.
and
Mehlig, B.
2016.
Statistical models for spatial patterns of heavy particles in turbulence.
Advances in Physics,
Vol. 65,
Issue. 1,
p.
1.
Yang, Kun
Zhao, Lihao
and
Andersson, Helge I.
2017.
Preferential particle concentration in wall-bounded turbulence with zero skin friction.
Physics of Fluids,
Vol. 29,
Issue. 11,
Yuan, Wenjun
Zhao, Lihao
Andersson, Helge I.
and
Deng, Jianqiang
2018.
Three-dimensional Voronoï analysis of preferential concentration of spheroidal particles in wall turbulence.
Physics of Fluids,
Vol. 30,
Issue. 6,
Lawson, John M.
Bodenschatz, Eberhard
Lalescu, Cristian C.
and
Wilczek, Michael
2018.
Bias in particle tracking acceleration measurement.
Experiments in Fluids,
Vol. 59,
Issue. 11,
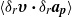 was observed to increase significantly with particle inertia for identical flow conditions. We show that this increase is related to a preferential alignment between these dynamical quantities. With increasing particle density the probability for those two vectors to be collinear was observed to grow. We show that these results are consistent with the preferential sampling of strain-dominated regions by inertial particles.
was observed to increase significantly with particle inertia for identical flow conditions. We show that this increase is related to a preferential alignment between these dynamical quantities. With increasing particle density the probability for those two vectors to be collinear was observed to grow. We show that these results are consistent with the preferential sampling of strain-dominated regions by inertial particles.
