Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yang, X. I. A.
Baidya, R.
Johnson, P.
Marusic, I.
and
Meneveau, C.
2017.
Structure function tensor scaling in the logarithmic region derived from the attached eddy model of wall-bounded turbulent flows.
Physical Review Fluids,
Vol. 2,
Issue. 6,
Morrill-Winter, C.
Squire, D. T.
Klewicki, J. C.
Hutchins, N.
Schultz, M. P.
and
Marusic, I.
2017.
Reynolds number and roughness effects on turbulent stresses in sandpaper roughness boundary layers.
Physical Review Fluids,
Vol. 2,
Issue. 5,
Gremes-Cordero, Silvia
2017.
Observations of turbulent kinetic energy dissipation at the Labrador Sea surface layer.
The International Journal of Ocean and Climate Systems,
Vol. 8,
Issue. 3,
p.
161.
Carter, Douglas W.
and
Coletti, Filippo
2017.
Scale-to-scale anisotropy in homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 827,
Issue. ,
p.
250.
Yang, X. I. A.
and
Howland, M. F.
2018.
Implication of Taylor’s hypothesis on measuring flow modulation.
Journal of Fluid Mechanics,
Vol. 836,
Issue. ,
p.
222.
Barros, Julio M.
and
Christensen, Kenneth T.
2019.
Characteristics of large-scale and superstructure motions in a turbulent boundary layer overlying complex roughness.
Journal of Turbulence,
Vol. 20,
Issue. 2,
p.
147.
Jurčáková, Klára
and
Kellnerová, Radka
2019.
Progress in Turbulence VIII.
Vol. 226,
Issue. ,
p.
93.
Rubio Carpio, Alejandro
Merino Martínez, Roberto
Avallone, Francesco
Ragni, Daniele
Snellen, Mirjam
and
van der Zwaag, Sybrand
2019.
Experimental characterization of the turbulent boundary layer over a porous trailing edge for noise abatement.
Journal of Sound and Vibration,
Vol. 443,
Issue. ,
p.
537.
Li, Mogeng
de Silva, Charitha M.
Rouhi, Amirreza
Baidya, Rio
Chung, Daniel
Marusic, Ivan
and
Hutchins, Nicholas
2019.
Recovery of wall-shear stress to equilibrium flow conditions after a rough-to-smooth step change in turbulent boundary layers.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
472.
Treumann, R. A.
Baumjohann, W.
and
Narita, Y.
2019.
On the applicability of Taylor’s hypothesis in streaming magnetohydrodynamic turbulence.
Earth, Planets and Space,
Vol. 71,
Issue. 1,
Choi, Yun Kyung
Hwang, Hyeon Gyu
Lee, Young Mo
and
Lee, Jae Hwa
2020.
Effects of the roughness height in turbulent boundary layers over rod- and cuboid-roughened walls.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108644.
Voskoboinik, V. A.
Voskoboinik, A. A.
Turik, V. N.
and
Voskoboinik, A. V.
2020.
Space and Time Characteristics of the Velocity and Pressure Fields of the Fluid Flow Inside a Hemispherical Dimple Generator of Vortices.
Journal of Engineering Physics and Thermophysics,
Vol. 93,
Issue. 5,
p.
1205.
Farkas, Andrea
Degiuli, Nastia
and
Martić, Ivana
2020.
An investigation into the effect of hard fouling on the ship resistance using CFD.
Applied Ocean Research,
Vol. 100,
Issue. ,
p.
102205.
Liu, Chang
and
Gayme, Dennice F.
2020.
An input–output based analysis of convective velocity in turbulent channels.
Journal of Fluid Mechanics,
Vol. 888,
Issue. ,
Li, Mogeng
de Silva, Charitha M.
Chung, Daniel
Pullin, Dale I.
Marusic, Ivan
and
Hutchins, Nicholas
2021.
Experimental study of a turbulent boundary layer with a rough-to-smooth change in surface conditions at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 923,
Issue. ,
Beresh, Steven J
2021.
Time-resolved particle image velocimetry.
Measurement Science and Technology,
Vol. 32,
Issue. 10,
p.
102003.
Ghanadi, F.
and
Djenidi, L.
2021.
Reynolds number effect on the response of a rough wall turbulent boundary layer to local wall suction.
Journal of Fluid Mechanics,
Vol. 916,
Issue. ,
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Zhang, Peng
and
Li, Danxun
2021.
Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Liu, Hongyou
and
Zheng, Xiaojing
2021.
Large-scale structures of wall-bounded turbulence in single- and two-phase flows: advancing understanding of the atmospheric surface layer during sandstorms.
Flow,
Vol. 1,
Issue. ,
Everard, K. A.
Katul, G. G.
Lawrence, G. A.
Christen, A.
and
Parlange, M. B.
2021.
Sweeping Effects Modify Taylor’s Frozen Turbulence Hypothesis for Scalars in the Roughness Sublayer.
Geophysical Research Letters,
Vol. 48,
Issue. 22,
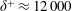 $\unicode[STIX]{x1D6FF}^{+}\approx 12\,000$ ). For each wall condition, temporal and true spatial descriptions of the same flow are available from hot-wire anemometry and high-spatial-range particle image velocimetry, respectively. The results show that over the resolved flow domain, which is limited to a streamwise length of twice the boundary layer thickness, true spatial spectra of smooth-wall streamwise and wall-normal velocity fluctuations agree, to within experimental uncertainty, with those obtained from time series using Taylor’s frozen turbulence hypothesis (Proc. R. Soc. Lond. A, vol. 164, 1938, pp. 476–490). The same applies for the streamwise velocity spectra on rough walls. For the wall-normal velocity spectra, however, clear differences are observed between the true spatial and temporally convected spectra. For the rough-wall spectra, a correction is derived to enable accurate prediction of wall-normal velocity length scales from measurements of their time scales, and the implications of this correction are considered. Potential violations to Taylor’s hypothesis in flows above perturbed walls may help to explain conflicting conclusions in the literature regarding the effect of near-wall modifications on outer-region flow. In this regard, all true spatial and corrected spectra presented here indicate structural similarity in the outer region of smooth- and rough-wall flows, providing evidence for Townsend’s wall-similarity hypothesis (The Structure of Turbulent Shear Flow, vol. 1, 1956).
$\unicode[STIX]{x1D6FF}^{+}\approx 12\,000$ ). For each wall condition, temporal and true spatial descriptions of the same flow are available from hot-wire anemometry and high-spatial-range particle image velocimetry, respectively. The results show that over the resolved flow domain, which is limited to a streamwise length of twice the boundary layer thickness, true spatial spectra of smooth-wall streamwise and wall-normal velocity fluctuations agree, to within experimental uncertainty, with those obtained from time series using Taylor’s frozen turbulence hypothesis (Proc. R. Soc. Lond. A, vol. 164, 1938, pp. 476–490). The same applies for the streamwise velocity spectra on rough walls. For the wall-normal velocity spectra, however, clear differences are observed between the true spatial and temporally convected spectra. For the rough-wall spectra, a correction is derived to enable accurate prediction of wall-normal velocity length scales from measurements of their time scales, and the implications of this correction are considered. Potential violations to Taylor’s hypothesis in flows above perturbed walls may help to explain conflicting conclusions in the literature regarding the effect of near-wall modifications on outer-region flow. In this regard, all true spatial and corrected spectra presented here indicate structural similarity in the outer region of smooth- and rough-wall flows, providing evidence for Townsend’s wall-similarity hypothesis (The Structure of Turbulent Shear Flow, vol. 1, 1956).

