Published online by Cambridge University Press: 11 January 2016
We revisit, both numerically and analytically, the finite-time blowup of the infinite-energy solution of 3D Euler equations of stagnation-point type introduced by Gibbon et al. (Physica D, vol. 132, 1999, pp. 497–510). By employing the method of mapping to regular systems, presented by Bustamante (Physica D, vol. 240 (13), 2011, pp. 1092–1099) and extended to the symmetry-plane case by Mulungye et al. (J. Fluid Mech., vol. 771, 2015, pp. 468–502), we establish a curious property of this solution that was not observed in early studies: before but near singularity time, the blowup goes from a fast transient to a slower regime that is well resolved spectrally, even at mid-resolutions of 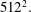 $512^{2}.$ This late-time regime has an atypical spectrum: it is Gaussian rather than exponential in the wavenumbers. The analyticity-strip width decays to zero in a finite time, albeit so slowly that it remains well above the collocation-point scale for all simulation times
$512^{2}.$ This late-time regime has an atypical spectrum: it is Gaussian rather than exponential in the wavenumbers. The analyticity-strip width decays to zero in a finite time, albeit so slowly that it remains well above the collocation-point scale for all simulation times 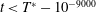 $t<T^{\ast }-10^{-9000}$, where
$t<T^{\ast }-10^{-9000}$, where 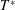 $T^{\ast }$ is the singularity time. Reaching such a proximity to singularity time is not possible in the original temporal variable, because floating-point double precision (
$T^{\ast }$ is the singularity time. Reaching such a proximity to singularity time is not possible in the original temporal variable, because floating-point double precision (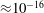 ${\approx}10^{-16}$) creates a ‘machine-epsilon’ barrier. Due to this limitation on the original independent variable, the mapped variables now provide an improved assessment of the relevant blowup quantities, crucially with acceptable accuracy at an unprecedented closeness to the singularity time:
${\approx}10^{-16}$) creates a ‘machine-epsilon’ barrier. Due to this limitation on the original independent variable, the mapped variables now provide an improved assessment of the relevant blowup quantities, crucially with acceptable accuracy at an unprecedented closeness to the singularity time: 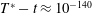 $T^{\ast }-t\approx 10^{-140}$.
$T^{\ast }-t\approx 10^{-140}$.