Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-15T23:28:33.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Axisymmetric inertial modes in a spherical shell at low Ekman numbers

Published online by Cambridge University Press:  06 April 2018

M. Rieutord Open the ORCID record for M. Rieutord [Opens in a new window]  and
L. Valdettaro
M. Rieutord*
Affiliation:
Université de Toulouse, UPS-OMP, IRAP, Toulouse, France CNRS, IRAP, 14 avenue Edouard Belin, F-31400 Toulouse, France
L. Valdettaro
Affiliation:
MOX, Dipartimento di Matematica, Politecnico di Milano, Piazza L. da Vinci, 32, 20133 Milano, Italy
*
†Email address for correspondence: mrieutord@irap.omp.eu
Get access Rights & Permissions [Opens in a new window]

Abstract

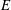We investigate the asymptotic properties of axisymmetric inertial modes propagating in a spherical shell when viscosity tends to zero. We identify three kinds of eigenmodes whose eigenvalues follow very different laws as the Ekman number $E$ becomes very small. First are modes associated with attractors of characteristics that are made of thin shear layers closely following the periodic orbit traced by the characteristic attractor. Second are modes made of shear layers that connect the critical latitude singularities of the two hemispheres of the inner boundary of the spherical shell. Third are quasi-regular modes associated with the frequency of neutral periodic orbits of characteristics. We thoroughly analyse a subset of attractor modes for which numerical solutions point to an asymptotic law governing the eigenvalues. We show that three length scales proportional to 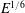$E^{1/6}$, 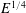$E^{1/4}$ and 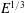$E^{1/3}$ control the shape of the shear layers that are associated with these modes. These scales point out the key role of the small parameter 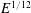$E^{1/12}$ in these oscillatory flows. With a simplified model of the viscous Poincaré equation, we can give an approximate analytical formula that reproduces the velocity field in such shear layers. Finally, we also present an analysis of the quasi-regular modes whose frequencies are close to 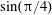$\sin (\unicode[STIX]{x03C0}/4)$ and explain why a fluid inside a spherical shell cannot respond to any periodic forcing at this frequency when viscosity vanishes.

JFM classification

Boundary Layers: Free shear layers Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 844 , 10 June 2018 , pp. 597 - 634
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Backus, G. & Rieutord, M. 2017 Completeness of inertial modes of an incompressible inviscid fluid in a corotating ellipsoid. Phys. Rev. E 95 (5), 053116.Google Scholar
Baruteau, C. & Rieutord, M. 2013 Inertial waves in a differentially rotating spherical shell – I. Free modes of oscillation. J. Fluid Mech. 719, 47–81.10.1017/jfm.2012.605Google Scholar
Bryan, G. 1889 The waves on a rotating liquid spheroid of finite ellipticity. Phil. Trans. R. Soc. Lond. 180, 187–219.Google Scholar
Chatelin, F. 2012 Eigenvalues of Matrices, Revised edn. SIAM Classics in Applied Mathematics.10.1137/1.9781611972467Google Scholar
Cui, Z., Zhang, K. & Liao, X. 2014 On the completeness of inertial wave modes in rotating annular channels. Geophys. Astrophys. Fluid Dyn. 108, 44–59.10.1080/03091929.2013.821117Google Scholar
Dintrans, B., Rieutord, M. & Valdettaro, L. 1999 Gravito-inertial waves in a rotating stratified sphere or spherical shell. J. Fluid Mech. 398, 271–297.10.1017/S0022112099006308Google Scholar
Fotheringham, P. & Hollerbach, R. 1998 Inertial oscillations in a spherical shell. Geophys. Astrophys. Fluid Dyn. 89, 23–43.10.1080/03091929808213647Google Scholar
Friedlander, S. 1982 Turning surface behaviour for internal waves subject to general gravitational fields. Geophys. Astrophys. Fluid Dyn. 21, 189–200.10.1080/03091928208209012Google Scholar
Friedlander, S. & Siegmann, W. 1982 Internal waves in a contained rotating stratified fluid. J. Fluid Mech. 114, 123–156.10.1017/S002211208200007XGoogle Scholar
Gerkema, T., Zimmerman, J. T. F., Maas, L. R. M. & van Haren, H. 2008 Geophysical and astrophysical fluid dynamics beyond the traditional approximation. Rev. Geophys. 46, RG2004.10.1029/2006RG000220Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hollerbach, R. & Kerswell, R. 1995 Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 298, 327–339.10.1017/S0022112095003338Google Scholar
Ivers, D. J., Jackson, A. & Winch, D. 2015 Enumeration, orthogonality and completeness of the incompressible Coriolis modes in a sphere. J. Fluid Mech. 766, 468–498.10.1017/jfm.2015.27Google Scholar
Kelvin, Lord 1880 Vibrations of a columnar vortex. Phil. Mag. 10, 155–168.Google Scholar
Kerswell, R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.10.1017/S0022112095003326Google Scholar
Le Dizès, S. 2015 Wave field and zonal flow of a librating disk. J. Fluid Mech. 782, 178–208.10.1017/jfm.2015.530Google Scholar
Maas, L., Benielli, D., Sommeria, J. & Lam, F.-P. 1997 Observation of an internal wave attractor in a confined, stably stratified fluid. Nature 388, 557–561.10.1038/41509Google Scholar
Maas, L. & Lam, F.-P. 1995 Geometric focusing of internal waves. J. Fluid Mech. 300, 1–41.10.1017/S0022112095003582Google Scholar
Manders, A. M. M. & Maas, L. R. M. 2003 Observations of inertial waves in a rectangular basin with one sloping boundary. J. Fluid Mech. 493, 59–88.10.1017/S0022112003005998Google Scholar
Mirouh, G. M., Baruteau, C., Rieutord, M. & Ballot, 2016 Gravito-inertial waves in a differentially rotating spherical shell. J. Fluid Mech. 800, 213–247.10.1017/jfm.2016.382Google Scholar
Noir, J., Brito, D., Aldridge, K. & Cardin, P. 2001 Experimental evidence of inertial waves in a precessing spheroidal cavity. Geophys. Res. Lett. 28, 3785–3788.10.1029/2001GL012956Google Scholar
Ogilvie, G. 2009 Tidal dissipation in rotating fluid bodies: a simplified model. Mon. Not. R. Astron. Soc. 396, 794–806.10.1111/j.1365-2966.2009.14814.xGoogle Scholar
Ogilvie, G. I. & Lin, D. N. C. 2004 Tidal dissipation in rotating giant planets. Astrophys. J. 610, 477–509.10.1086/421454Google Scholar
Poincaré, H. 1885 Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation. Acta Mathematica 7, 259–380.10.1007/BF02402204Google Scholar
Rieutord, M. 1987 Linear theory of rotating fluids using spherical harmonics. I. Steady flows. Geophys. Astrophys. Fluid Dyn. 39, 163–182.10.1080/03091928708208811Google Scholar
Rieutord, M. 2015 Fluid Dynamics: An Introduction. Springer.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2000 Waves attractors in rotating fluids: a paradigm for ill-posed cauchy problems. Phys. Rev. Lett. 85, 4277–4280.10.1103/PhysRevLett.85.4277Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.10.1017/S0022112001003718Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.10.1017/S0022112097005491Google Scholar
Rieutord, M. & Valdettaro, L. 2010 Viscous dissipation by tidally forced inertial modes in a rotating spherical shell. J. Fluid Mech. 643, 363–394.10.1017/S002211200999214XGoogle Scholar
Rieutord, M., Valdettaro, L. & Georgeot, B. 2002 Analysis of singular inertial modes in a spherical shell: the slender toroidal shell model. J. Fluid Mech. 463, 345–360.10.1017/S0022112002008881Google Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.10.1017/jfm.2012.604Google Scholar
Stewartson, K. & Rickard, J. 1969 Pathological oscillations of a rotating fluid. J. Fluid Mech. 35, 759–773.10.1017/S002211206900142XGoogle Scholar
Valdettaro, L., Rieutord, M., Braconnier, T. & Fraysse, V. 2007 Convergence and round-off errors in a two-dimensional eigenvalue problem using spectral methods and Arnoldi–Chebyshev algorithm. J. Comput. Appl. Maths 205, 382–393.10.1016/j.cam.2006.05.009Google Scholar
Zhang, K.-K., Earnshaw, P., Liao, X. & Busse, F. 2001 On inertial waves in a rotating sphere. J. Fluid Mech. 437, 2001.10.1017/S0022112001004049Google Scholar