Hostname: page-component-68c7f8b79f-m4fzj Total loading time: 0 Render date: 2025-12-17T18:47:11.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Bistability of bubble and conical forms of vortex breakdown in laminar swirling jets

Published online by Cambridge University Press:  27 February 2020

Pradeep Moise Open the ORCID record for Pradeep Moise [Opens in a new window]
Pradeep Moise*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Science, Bengaluru560012, India
*
†Email address for correspondence: pradeep890@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

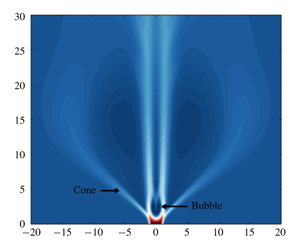
Vortex breakdown (VB) in swirling jets can be classified as either a bubble (BVB) or a conical (CVB) form based on the shape of its recirculation zone. The present study investigates the hysteresis features of these forms in laminar swirling jets using direct numerical simulations. It is established here that BVB and CVB are bistable forms in a large swirl range and for a Reynolds number of 200 (based on jet radius and centreline velocity). Considerable differences were observed in the length scales associated with the two, with the approximate recirculation zone diameters of the BVB and CVB being 1 and 15 jet diameters, respectively. Additionally, two types of BVB were observed, identified as a two-celled BVB with spiral tail and an asymmetric BVB. The former is characterized by an almost steady bubble with a two-celled structure. By contrast, the entire bubble envelope oscillated in a non-axisymmetric fashion for the latter. These two types of BVB themselves were found to coexist in a small swirl range. A global linear stability analysis was used to show that two different unstable single helical modes are associated with these two types. In comparison to using the base flow, a stability analysis performed on the mean flow was found to predict the coherent features of asymmetric BVB observed in the simulations more precisely. This study highlights the rich variety of VB flow states that coexist in various ranges of swirl strengths and the significance of hysteresis effects in laminar swirling jets.

JFM classification

Vortex Flows: Vortex breakdown

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 889 , 25 April 2020 , A31
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, B., Jones, M., Hourigan, K. & Thompson, M. 1999 Hysteresis in the open pipe flow with vortex breakdown. In 2nd International Conference on CFD in the Minerals and Process Industries, pp. 311–316.Google Scholar
Aguilar, M., Malanoski, M., Adhitya, G., Emerson, B., Acharya, V., Noble, D. & Lieuwen, T. 2015 Helical flow disturbances in a multinozzle combustor. Trans. ASME J. Engng Gas Turbines Power 137 (9), 091507.CrossRefGoogle Scholar
Åkervik, E., Brandt, L., Henningson, D. S., Hœpffner, J., Marxen, O. & Schlatter, P. 2006 Steady solutions of the Navier–Stokes equations by selective frequency damping. Phys. Fluids 18 (6), 068102.CrossRefGoogle Scholar
Balakrishna, N., Mathew, J. & Samanta, A. 2019 Inviscid and viscous global stability of vortex rings. J. Fluid Mech. (submitted).Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750–756.CrossRefGoogle Scholar
Bayliss, A. & Turkel, E. 1992 Mappings and accuracy for Chebyshev pseudo-spectral approximations. J. Comput. Phys. 101 (2), 349–359.CrossRefGoogle Scholar
Beran, P. S. & Culick, F. E. C. 1992 The role of non-uniqueness in the development of vortex breakdown in tubes. J. Fluid Mech. 242, 491–527.CrossRefGoogle Scholar
Billant, P., Chomaz, J.-M. & Huerre, P. 1998 Experimental study of vortex breakdown in swirling jets. J. Fluid Mech. 376, 183–219.CrossRefGoogle Scholar
Brown, G. L. & Lopez, J. M. 1990 Axisymmetric vortex breakdown. Part 2. Physical mechanisms. J. Fluid Mech. 221, 553–576.CrossRefGoogle Scholar
Brücker, C. 1993 Study of vortex breakdown by particle tracking velocimetry (PTV). Part 2. Spiral-type vortex breakdown. Exp. Fluids 14 (1–2), 133–139.CrossRefGoogle Scholar
Brücker, C. & Althaus, W. 1992 Study of vortex breakdown by particle tracking velocimetry (PTV). Exp. Fluids 13 (5), 339–349.CrossRefGoogle Scholar
Burggraf, O. R. & Foster, M. R. 1977 Continuation or breakdown in tornado-like vortices. J. Fluid Mech. 80 (June 1976), 685–703.CrossRefGoogle Scholar
Darmofal, D. L. 1996 Comparisons of experimental and numerical results for axisymmetric vortex breakdown in pipes. Comput. Fluids 25 (4), 353–371.CrossRefGoogle Scholar
Escudier, M. 1984 Observations of the flow produced in a cylindrical container by a rotating endwall. Exp. Fluids 2 (4), 189–196.CrossRefGoogle Scholar
Escudier, M. 1988 Vortex breakdown: observations and explanations. Prog. Aerosp. Sci. 25 (2), 189–229.CrossRefGoogle Scholar
Faler, J. H. & Leibovich, S. 1977 Disrupted states of vortex flow and vortex breakdown. Phys. Fluids 20 (9), 1385–1400.CrossRefGoogle Scholar
Faler, J. H. & Leibovich, S. 1978 An experimental map of the internal structure of a vortex breakdown. J. Fluid Mech. 86, 313–335.CrossRefGoogle Scholar
Falese, M., Gicquel, L. Y. M. & Poinsot, T. 2014 LES of bifurcation and hysteresis in confined annular swirling flows. Comput. Fluids 89, 167–178.CrossRefGoogle Scholar
Fitzgerald, A. J., Hourigan, K. & Thompson, M. C. 2004 Towards a universal criterion for predicting vortex breakdown in swirling jets. In Proceedings of the Fifteenth Australasian Fluid Mechanics Conference (ed. Behnia, M., Lin, W. & McBain, G. D.). The University of Sydney.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003 Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.CrossRefGoogle Scholar
Gallaire, F., Rott, S. & Chomaz, J.-M. 2004 Experimental study of a free and forced swirling jet. Phys. Fluids 16 (8), 2907–2917.CrossRefGoogle Scholar
Gore, R. W. & Ranz, W. E. 1964 Backflows in rotating fluids moving axially through expanding cross sections. AIChE J. 10 (1), 83–88.CrossRefGoogle Scholar
Grabowski, W. J. & Berger, S. A. 1976 Solutions of the Navier–Stokes equations for vortex breakdown. J. Fluid Mech. 75 (3), 525–544.CrossRefGoogle Scholar
Hall, M. G. 1972 Vortex breakdown. Annu. Rev. Fluid Mech. 4 (1), 195–218.CrossRefGoogle Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jiang, T. L. & Shen, C. H. 1994 Numerical predictions of the bifurcation of confined swirling flows. Int. J. Numer. Meth. Fluids 19 (11), 961–979.CrossRefGoogle Scholar
Jordi, B. E., Cotter, C. J. & Sherwin, S. J. 2014 Encapsulated formulation of the selective frequency damping method. Phys. Fluids 26 (3), 034101.CrossRefGoogle Scholar
Kurosaka, M., Kikuchi, M., Hirano, K., Yuge, T. & Inoue, H. 2003 Interchangeability of vortex-breakdown types. Exp. Fluids 34 (1), 77–86.CrossRefGoogle Scholar
Laizet, S. & Lamballais, E. 2009 High-order compact schemes for incompressible flows: a simple and efficient method with quasi-spectral accuracy. J. Comput. Phys. 228 (16), 5989–6015.CrossRefGoogle Scholar
Laizet, S. & Li, N. 2011 Incompact3d, a powerful tool to tackle turbulence problems with up to O (105) computational cores. Intl J. Numer. Meth. Fluids 67, 1735–1757.CrossRefGoogle Scholar
Lamballais, E., Fortuné, V. & Laizet, S. 2011 Straightforward high-order numerical dissipation via the viscous term for direct and large eddy simulation. J. Comput. Phys. 230 (9), 3270–3275.CrossRefGoogle Scholar
Lambourne, N. C. & Bryer, D. W.1961 The bursting of leading-edge vortices – some observations and discussion of the phenomenon. Tech. Rep. ARC Reports and Memoranda No. 3282.Google Scholar
Leibovich, S. 1978 The structure of vortex breakdown. Annu. Rev. Fluid Mech. 10, 221–246.CrossRefGoogle Scholar
Leibovich, S. 1984 Vortex stability and breakdown – survey and extension. AIAA J. 22 (9), 1192–1206.CrossRefGoogle Scholar
Leibovich, S. & Kribus, A. 1990 Large-amplitude wavetrains and solitary waves in vortices. J. Fluid Mech. 216, 459–504.CrossRefGoogle Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.CrossRefGoogle Scholar
Lopez, J. M. 1995 Unsteady swirling flow in an enclosed cylinder with reflectional symmetry. Phys. Fluids 7 (11), 2700–2714.CrossRefGoogle Scholar
Lucca-Negro, O. & O’Doherty, T. 2001 Vortex breakdown: a review. Prog. Energy Combust. Sci. 27 (4), 431–481.CrossRefGoogle Scholar
Lumley, J. L. 1970 Stochastic Tools in Turbulence, 1st edn. Academic Press.Google Scholar
Meliga, P., Gallaire, F. & Chomaz, J.-M. 2012 A weakly nonlinear mechanism for mode selection in swirling jets. J. Fluid Mech. 699, 216–262.CrossRefGoogle Scholar
Moise, P. & Mathew, J. 2019 Bubble and conical forms of vortex breakdown in swirling jets. J. Fluid Mech. 873, 322–357.CrossRefGoogle Scholar
Mourtazin, D. & Cohen, J. 2007 The effect of buoyancy on vortex breakdown in a swirling jet. J. Fluid Mech. 571, 177–189.CrossRefGoogle Scholar
Ogus, G., Baelmans, M. & Vanierschot, M. 2016 On the flow structures and hysteresis of laminar swirling jets. Phys. Fluids 28 (12), 123604.CrossRefGoogle Scholar
Pradeep, M.2019 Bubble and conical forms of vortex breakdown in swirling jets. PhD thesis, Indian Institute of Science.Google Scholar
Rajamanickam, K. & Basu, S. 2018 Insights into the dynamics of conical breakdown modes in coaxial swirling flow field. J. Fluid Mech. 853, 72–110.CrossRefGoogle Scholar
Reynolds, W. C., Parekh, D. E., Juvet, P. J. D. & Lee, M. J. D. 2003 Bifurcating and blooming jets. Annu. Rev. Fluid Mech. 35 (1), 295–315.CrossRefGoogle Scholar
Ruith, M. R., Chen, P. & Meiburg, E. 2004 Development of boundary conditions for direct numerical simulations of three-dimensional vortex breakdown phenomena in semi-infinite domains. Comput. Fluids 33 (9), 1225–1250.CrossRefGoogle Scholar
Ruith, M. R., Chen, P., Meiburg, E. & Maxworthy, T. 2003 Three-dimensional vortex breakdown in swirling jets and wakes: direct numerical simulation. J. Fluid Mech. 486, 331–378.CrossRefGoogle Scholar
Santhosh, R. & Basu, S. 2015 Acoustic response of vortex breakdown modes in a coaxial isothermal unconfined swirling jet. Phys. Fluids 27 (3), 033601.CrossRefGoogle Scholar
Sarpkaya, T. 1971 On stationary and travelling vortex breakdowns. J. Fluid Mech. 45 (3), 545–559.CrossRefGoogle Scholar
Sarpkaya, T. 1995 Turbulent vortex breakdown. Phys. Fluids 7 (10), 2301–2303.CrossRefGoogle Scholar
Shtern, V. 2004 Bifurcation of conical magnetic field. Phys. Rev. E 69 (6), 065301.CrossRefGoogle ScholarPubMed
Shtern, V. & Hussain, F. 1993 Hysteresis in a swirling jet as a model tornado. Phys. Fluids A Fluid Dyn. 5 (9), 2183–2195.CrossRefGoogle Scholar
Shtern, V. & Hussain, F. 1999 Collapse, symmetry breaking, and hysteresis in swirling flows. Annu. Rev. Fluid Mech. 31 (1), 537–566.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Stevens, J. L., Lopez, J. M. & Cantwell, B. J. 1999 Oscillatory flow states in an enclosed cylinder with a rotating endwall. J. Fluid Mech. 389, 101–118.CrossRefGoogle Scholar
Syred, N. & Beer, J. M. 1974 Combustion in swirling flows: a review. Combust. Flame 23 (2), 143–201.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M. P. 2016 Coherent structures in a swirl injector at Re = 4800 by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Towne, A., Schmidt, O. T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Vanierschot, M., Müller, J. S., Sieber, M., Percin, M., van Oudheusden, B. W. & Oberleithner, K. 2020 Single- and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow. J. Fluid Mech. 883, A31.CrossRefGoogle Scholar
Vanierschot, M. & Van den Bulck, E. 2007a Hysteresis in flow patterns in annular swirling jets. Exp. Therm. Fluid Sci. 31 (6), 513–524.CrossRefGoogle Scholar
Vanierschot, M. & Van den Bulck, E. 2007b Numerical study of hysteresis in annular swirling jets with a stepped-conical nozzle. Intl J. Numer. Meth. Fluids 54 (3), 313–324.CrossRefGoogle Scholar
Vanoverberghe, K. P., Van den Bulck, E. V., Tummers, M. J. & Hübner, W. A. 2002 Multiflame patterns in swirl-driven partially premixed natural gas combustion. Trans. ASME J. Engng Gas Turbines Power 125 (1), 40–45.CrossRefGoogle Scholar
Vishwanath, R. B., Tilak, P. M. & Chaudhuri, S. 2018 An experimental study of interacting swirl flows in a model gas turbine combustor. Exp. Fluids 59 (3), 38.CrossRefGoogle Scholar
Wang, S. & Rusak, Z. 1997 The dynamics of a swirling flow in a pipe and transition to axisymmetric vortex breakdown. J. Fluid Mech. 340, 177–223.CrossRefGoogle Scholar

Moise supplementary movie

Contours of vorticity magnitude on the z = 0 plane at different times for the asymmetric type of BVB observed for S = 1.7, showing the oscillation of the entire bubble envelope, a characteristic of this BVB type.

Download Moise supplementary movie(Video)
Video 13.1 MB