Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-08-03T01:36:52.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundary layers and wind in cylindrical Rayleigh–Bénard cells

Published online by Cambridge University Press:  06 March 2012

Sebastian Wagner ,
Olga Shishkina  and
Claus Wagner
Sebastian Wagner*
Affiliation:
German Aerospace Center (DLR), Institute of Aerodynamics and Flow Technology, Bunsenstrasse 10, 37073 Göttingen, Germany
Olga Shishkina
Affiliation:
German Aerospace Center (DLR), Institute of Aerodynamics and Flow Technology, Bunsenstrasse 10, 37073 Göttingen, Germany
Claus Wagner
Affiliation:
German Aerospace Center (DLR), Institute of Aerodynamics and Flow Technology, Bunsenstrasse 10, 37073 Göttingen, Germany
*
†Email address for correspondence: Sebastian.Wagner@DLR.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the wind and boundary layer properties of turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio one for Prandtl number 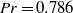and Rayleigh numbers (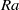) up to 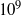by means of highly resolved direct numerical simulations. We identify time periods in which the orientation of the large-scale circulation (LSC) is nearly constant in order to perform a statistical analysis of the LSC. The analysis is then reduced to two dimensions by considering only the plane of the LSC. Within this plane the LSC is treated as a wind with thermal and viscous boundary layers developing close to the horizontal plates. Special focus is on the spatial development of the wind magnitude and the boundary layer thicknesses along the bottom plate. A method for the local analysis of the instantaneous boundary layer thicknesses is introduced which shows a dramatically changing wind magnitude along the wind path. Furthermore a linear increase of the viscous and thermal boundary layer thickness along the wind direction is observed for all 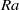considered while their ratio is spatially constant but depends weakly on 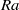. A possible explanation is a strong spatial variation of the wind magnitude and fluctuations in the boundary layer region.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent convection

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 697 , 25 April 2012 , pp. 336 - 366
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1. Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid Mech. 641, 157–167.Google Scholar
2. Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 82, 503–537.Google Scholar
3. Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
4. Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
5. Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.Google Scholar
6. Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
7. Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.Google Scholar
8. Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.CrossRefGoogle Scholar
9. Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale dynamics in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
10. Funfschilling, D., Brown, E. & Ahlers, G. 2008 Torsional oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 607, 119–139.Google Scholar
11. Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: A unifying view. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
12. Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
13. Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
14. Hartlep, T., Tilgner, A. & Busse, F. H. 2003 Large scale structures in Rayleigh–Bénard convection at high Rayleigh numbers. Phys. Rev. Lett. 91, 064501.Google Scholar
15. Hölling, M. & Herwig, H. 2006 Asymptotic analysis of heat transfer in turbulent Rayleigh–Bénard convection. Intl J. Heat Mass Transfer 49, 1129–1136.Google Scholar
16. Horn, S., Shishkina, O. & Wagner, C. 2011 The influence of non-Oberbeck–Boussinesq effects on rotating turbulent Rayleigh–Bénard convection. J. Phys.: Conf. Ser. 318, 082005.Google Scholar
17. Kaczorowski, M., Shishkina, O., Shishkin, A., Wagner, C. & Xia, K.-Q. 2011 Analysis of the large-scale circulation and the boundary layers in turbulent Rayleigh–Bénard convection. In Direct and Large-Eddy Simulation VIII (ed. Kuerten, H., Geurts, B., Armenio, V. & Fröhlich, J. ), pp. 383–388. Springer.CrossRefGoogle Scholar
18. Kraichnan, R. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
19. Kunnen, R. P. J., Clercx, H. J. H., Geurts, B. J., Bokhoven, L. J. A. V., Akkermans, R. A. D. & Verzicco, R. 2008 Numerical and experimental investigation of structure-function scaling in turbulent Rayleigh–Bénard convection. Phys. Rev. E 77, 016302.Google Scholar
20. Landau, L. D. & Lifschitz, E. M. 2007 Hydrodynamik. In Lehrbuch der theoretischen Physik, vol. 6, 5th edn. Harri Deutsch.Google Scholar
21. Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
22. Mishra, P. K., De, A. K., Verma, M. K. & Eswaran, V. 2011 Dynamics of re-orientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.Google Scholar
23. Niemela, J. J. & Sreenivasan, K. R. 2003 Confined turbulent convection. J. Fluid Mech. 481, 355–384.Google Scholar
24. du Puits, R., Resagk, C. & Thess, A. 2009 Structure of viscous boundary layers in turbulent Rayleigh–Bénard convection. Phys. Rev. E 80, 036318.Google Scholar
25. Resagk, C., du Puits, R., Thess, A., Dalzhansky, F. V., Grossmann, S., Araujo, F. F. & Lohse, D. 2006 Oszillations of the large-scale wind in turbulent thermal convection. Phys. Fluids 18, 095105.Google Scholar
26. Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2003 Heat transfer in turbulent Rayleigh–Bénard convection below the ultimate regime. J. Low Temp. Phys. 134, 1011–1042.Google Scholar
27. Schlichting, H. & Gersten, K. 2006 Grenzschicht-Theorie, 10th edn. Springer.Google Scholar
28. Schmalzl, J., Breuer, M. & Hansen, U. 2004 On the validity of two-dimensional numerical approaches to time-dependend thermal convection. Europhys. Lett. 67, 390–396.Google Scholar
29. Schmitt, L., Richter, K. & Friedrich, R. 1986 Large-eddy simulation of turbulent boundary layer and channel flow at high Reynolds number. In Direct and Large Eddy Simulation of Turbulence (ed. Schumann, U. & Friedrich, R. ). pp. 161–176. Vieweg.Google Scholar
30. Schumann, U. 1973 Ein Verfahren zur direkten numerischen Simulation turbulenter Strömungen in Platten- und Ringspaltkanälen und über seine Anwendung zur Untersuchung von Turbulenzmodellen. PhD thesis, TH Karlsruhe, KFK 1854.Google Scholar
31. Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
32. Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 663, 449–460.Google Scholar
33. Shishkina, O. & Wagner, C. 2005 A fourth-order accurate finite volume scheme for numerical simulations of turbulent Rayleigh–Bénard convection in cylindrical containers. C. R. Mecanique 333, 17–28.CrossRefGoogle Scholar
34. Shishkina, O. & Wagner, C. 2007 Local heat fluxes in turbulent Rayleigh–Bénard convection. Phys. Fluids 19, 085107.CrossRefGoogle Scholar
35. Shraiman, B. & Siggia, E. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.Google Scholar
36. Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2011a Effect of plumes on measuring the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 095110.Google Scholar
37. Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011b Prandtl and Rayleigh number dependence of heat transport in heigh Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.Google Scholar
38. Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.Google Scholar
39. Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
40. Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.Google Scholar
41. Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
42. Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47, 2253–2257.CrossRefGoogle ScholarPubMed
43. Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
44. Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T. S. & Xia, K.-Q. 2009 Origin of the temperature oscillations in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
45. Xia, K.-Q., Sun, C. & Zhou, S. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
46. Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
47. Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011 Horizontal structures of velocity and temperature boundary-layers in two-dimensional numerical turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 125104.CrossRefGoogle Scholar
48. Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
49. Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.CrossRefGoogle ScholarPubMed