1 Introduction
Capillary waves on a viscous fluid interface have recently been observed (Aarts, Schmidt & Lekkerkerker Reference Aarts, Schmidt and Lekkerkerker2004) to induce the spontaneous breakup of a thin liquid film and to control the inherent stochastic process of the submicron rupture event. Unlike gravity waves, these capillary waves have a short wavelength where the restoring force of surface tension dominates over the influence of gravity and can be found in the study of small-length-scale interfacial phenomena, for instance thin liquid films (Scheludko Reference Scheludko1967) and droplet coalescence (Blanchette & Bigioni Reference Blanchette and Bigioni2006). It is apparent that variations in surface tension can have dramatic knock-on effects on the dynamics of the capillary waves, with applications found in both surface chemistry (Edwards, Brenner & Wasan Reference Edwards, Brenner and Wasan1991) and interfacial fluid dynamics (Levich & Krylov Reference Levich and Krylov1969).
Surface-active materials, or surfactants, often lead to the formation of foams and emulsions by lowering the surface tension of a liquid interface (Levich & Krylov Reference Levich and Krylov1969; Edwards et al.
Reference Edwards, Brenner and Wasan1991; Batchelor et al.
Reference Batchelor, Moffatt, Worster and Osborn2003). Gradients of surfactant concentration (and therefore the surface tension coefficient) caused by dilatational deformations induce the Marangoni stress, which acts to oppose the changes in surface area and slows down the drainage and rupture processes of a thin liquid film. Moreover, the two-dimensional surfactant monolayer displays the rheological response, whereby shearing deformations can introduce an extra surface shear viscosity. In addition, a source of surface dilatational viscosity can result from the inherent compressibility of the two-dimensional surfactant monolayer (Zell et al.
Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014), in direct contrast to the incompressible Newtonian bulk fluid which can be characterised entirely by a single viscosity parameter
![]() $\unicode[STIX]{x1D707}$
. Furthermore, the dissipative nature of the surfactant adsorption–desorption kinetic process can also contribute towards the effective surface dilatational viscosity (Lucassen & Hansen Reference Lucassen and Hansen1966). With multiple sources of surface viscosities, we henceforth denote the effective surface dilatational and shear viscosities by
$\unicode[STIX]{x1D707}$
. Furthermore, the dissipative nature of the surfactant adsorption–desorption kinetic process can also contribute towards the effective surface dilatational viscosity (Lucassen & Hansen Reference Lucassen and Hansen1966). With multiple sources of surface viscosities, we henceforth denote the effective surface dilatational and shear viscosities by
![]() $\unicode[STIX]{x1D707}_{d}$
and
$\unicode[STIX]{x1D707}_{d}$
and
![]() $\unicode[STIX]{x1D707}_{s}$
respectively. Finally, we note that the magnitudes of
$\unicode[STIX]{x1D707}_{s}$
respectively. Finally, we note that the magnitudes of
![]() $\unicode[STIX]{x1D707}_{d}$
and
$\unicode[STIX]{x1D707}_{d}$
and
![]() $\unicode[STIX]{x1D707}_{s}$
need not be comparable (Djabbarah & Wasan Reference Djabbarah and Wasan1982), since they are each responsible for different physical processes. The physical manifestation of surface viscosity and its measurement remain controversial and subtle. For decades, the literature has been unable to agree on measurements of
$\unicode[STIX]{x1D707}_{s}$
need not be comparable (Djabbarah & Wasan Reference Djabbarah and Wasan1982), since they are each responsible for different physical processes. The physical manifestation of surface viscosity and its measurement remain controversial and subtle. For decades, the literature has been unable to agree on measurements of
![]() $\unicode[STIX]{x1D707}_{s}$
and
$\unicode[STIX]{x1D707}_{s}$
and
![]() $\unicode[STIX]{x1D707}_{d}$
. The chief difficulty lies with the fact that not only are surface viscosity and Marangoni effects intimately intwined (Levich & Krylov Reference Levich and Krylov1969; Scheid et al.
Reference Scheid, Delacotte, Dollet, Rio, Restagno, van Nierop, Cantat, Langevin and Stone2010; Langevin Reference Langevin2014), but experiments give the total characteristics for both the surface and bulk phases simultaneously and it is not trivial to extract the surface information a priori of the establishment of a particular surface model.
$\unicode[STIX]{x1D707}_{d}$
. The chief difficulty lies with the fact that not only are surface viscosity and Marangoni effects intimately intwined (Levich & Krylov Reference Levich and Krylov1969; Scheid et al.
Reference Scheid, Delacotte, Dollet, Rio, Restagno, van Nierop, Cantat, Langevin and Stone2010; Langevin Reference Langevin2014), but experiments give the total characteristics for both the surface and bulk phases simultaneously and it is not trivial to extract the surface information a priori of the establishment of a particular surface model.
For insoluble surface-active (surfactant) solutions, the intrinsic surface shear viscosity is clearly defined. However, for soluble surfactant solutions, in particular sodium dodecyl sulphate (SDS), the presence of a three-dimensional sublayer adjacent to the surface alters the rate of surface deformation (Stevenson Reference Stevenson2005), which may explain the numerous inconsistencies in the reported literature on the magnitudes of surface shear viscosities of surfactants. Some progress has been made recently, namely by the experimental work of Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014), in which the use of microbutton surface rheometry appears to yield relatively unambiguous measurements of the surface shear viscosity
![]() $\unicode[STIX]{x1D707}_{s}$
of SDS. These authors report an upper bound of
$\unicode[STIX]{x1D707}_{s}$
of SDS. These authors report an upper bound of
![]() $\unicode[STIX]{x1D707}_{s}\sim O(10^{-8}~\text{Nsm}^{-1})$
, which suggests that surface shear viscosity need not be the dominant surface phenomenon and that Marangoni effects and surface dilatational viscosity may also have effects.
$\unicode[STIX]{x1D707}_{s}\sim O(10^{-8}~\text{Nsm}^{-1})$
, which suggests that surface shear viscosity need not be the dominant surface phenomenon and that Marangoni effects and surface dilatational viscosity may also have effects.
In insoluble surfactant solutions, the surface shear viscosity is often much higher than
![]() $O(10^{-8}~\text{Nsm}^{-1})$
; in particular, in the case of 1-eicosanol, it is found (Gavranovic et al.
Reference Gavranovic, Kurtz, Golemanov, Lange and Fuller2006; Zell et al.
Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) to be at least
$O(10^{-8}~\text{Nsm}^{-1})$
; in particular, in the case of 1-eicosanol, it is found (Gavranovic et al.
Reference Gavranovic, Kurtz, Golemanov, Lange and Fuller2006; Zell et al.
Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) to be at least
![]() $10^{3}$
–
$10^{3}$
–
![]() $10^{4}$
times higher than that of soluble SDS solutions. Moreover, recent numerical (Gounley et al.
Reference Gounley, Boedec, Jaeger and Leonetti2016) and experimental studies have concluded that surface viscosity effects in insoluble surfactants can give rise to noticeable behaviours on the resulting dynamics, which cannot otherwise be fully understood if we consider the Marangoni effect alone (Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017). In this paper, we shall investigate both the Marangoni and surface viscosity effects in insoluble surfactant solutions with a particular focus on the dynamics of very thin films with capillary waves close to critical damping. For such a thin-film geometry of high wavenumber, we may consider a two-dimensional flow structure as well as a low Reynolds number under the Stokes limit. Foreshadowed by the previous numerical work (Gounley et al.
Reference Gounley, Boedec, Jaeger and Leonetti2016; Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017), we anticipate a similar importance of the Marangoni and surface viscosity effects on the capillary wave in the two-dimensional thin-film case under the Stokes limit.
$10^{4}$
times higher than that of soluble SDS solutions. Moreover, recent numerical (Gounley et al.
Reference Gounley, Boedec, Jaeger and Leonetti2016) and experimental studies have concluded that surface viscosity effects in insoluble surfactants can give rise to noticeable behaviours on the resulting dynamics, which cannot otherwise be fully understood if we consider the Marangoni effect alone (Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017). In this paper, we shall investigate both the Marangoni and surface viscosity effects in insoluble surfactant solutions with a particular focus on the dynamics of very thin films with capillary waves close to critical damping. For such a thin-film geometry of high wavenumber, we may consider a two-dimensional flow structure as well as a low Reynolds number under the Stokes limit. Foreshadowed by the previous numerical work (Gounley et al.
Reference Gounley, Boedec, Jaeger and Leonetti2016; Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017), we anticipate a similar importance of the Marangoni and surface viscosity effects on the capillary wave in the two-dimensional thin-film case under the Stokes limit.
In §§ 2–4, we extend the previous work of Prosperetti (Reference Prosperetti1976) and Shen et al. (Reference Shen, Denner, Morgan, van Wachem and Dini2017) to incorporate both surface shear and dilatational viscosity to the leading order, as described by the Boussinesq–Scriven model, into the dynamics of small-amplitude capillary waves. We delineate the effects of the convective–diffusive Marangoni stresses with surface viscosity effects in § 5. In § 6, we obtain an analytical form of the critical damping wavelength for the clean case considering only the bulk fluid viscosity. In § 7, we outline a numerical method to calculate the damping ratio of a general higher-ordered system and construct a minimal pole matrix to encode the information on the poles of the system with significant residue. Under this approach, we identify the transition point of the wave from an underdamped to an overdamped state of a general system and obtain numerically the correction to this critical wavelength by surface viscosity and Marangoni effects. The article is concluded in § 8.
2 Boussinesq–Scriven surface viscosity
Under the Boussinesq–Scriven model of surface viscosity (Scriven Reference Scriven1960; Aris Reference Aris1963; Slattery, Sagis & Oh Reference Slattery, Sagis and Oh2007), the surface stress boundary conditions at the interface between two Newtonian fluids can be written as
where
![]() $\unicode[STIX]{x1D64F}$
is the viscous stress tensor,
$\unicode[STIX]{x1D64F}$
is the viscous stress tensor,
![]() $\unicode[STIX]{x1D735}_{\!s}=\unicode[STIX]{x1D64B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the surface gradient operator for the projection tensor
$\unicode[STIX]{x1D735}_{\!s}=\unicode[STIX]{x1D64B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
is the surface gradient operator for the projection tensor
![]() $\unicode[STIX]{x1D64B}=\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n}^{T}$
with normal vector
$\unicode[STIX]{x1D64B}=\unicode[STIX]{x1D644}-\boldsymbol{n}\boldsymbol{n}^{T}$
with normal vector
![]() $\boldsymbol{n}$
,
$\boldsymbol{n}$
,
![]() $[\cdot ]$
denotes the jump in magnitude across the interface and
$[\cdot ]$
denotes the jump in magnitude across the interface and
![]() $\unicode[STIX]{x1D748}_{s}$
is the surface viscous stress tensor, defined by
$\unicode[STIX]{x1D748}_{s}$
is the surface viscous stress tensor, defined by
where
is the surface rate of deformation tensor. The divergence of
![]() $\unicode[STIX]{x1D748}_{s}$
may be written (Scriven Reference Scriven1960) in the form
$\unicode[STIX]{x1D748}_{s}$
may be written (Scriven Reference Scriven1960) in the form
 $$\begin{eqnarray}\displaystyle [\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}] & = & \displaystyle \unicode[STIX]{x1D735}_{\!s}\unicode[STIX]{x1D70E}+(\unicode[STIX]{x1D707}_{d}+\unicode[STIX]{x1D707}_{s})\unicode[STIX]{x1D735}_{\!s}(\unicode[STIX]{x1D735}_{\!s}\boldsymbol{\cdot }\boldsymbol{u}_{s})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D707}_{s}[2K\boldsymbol{u}_{s}+\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\!s}\times \boldsymbol{u}_{s})+2(\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}\boldsymbol{n}\times \boldsymbol{n})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\!s}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n})]\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{n}[2H\unicode[STIX]{x1D70E}+2H(\unicode[STIX]{x1D707}_{d}+\unicode[STIX]{x1D707}_{s})\unicode[STIX]{x1D735}_{\!s}\boldsymbol{\cdot }\boldsymbol{u}_{s}-2\unicode[STIX]{x1D707}_{s}(\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}\boldsymbol{n}\times \boldsymbol{n})\boldsymbol{ : }\unicode[STIX]{x1D735}_{\!s}\boldsymbol{u}_{s}],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D64F}] & = & \displaystyle \unicode[STIX]{x1D735}_{\!s}\unicode[STIX]{x1D70E}+(\unicode[STIX]{x1D707}_{d}+\unicode[STIX]{x1D707}_{s})\unicode[STIX]{x1D735}_{\!s}(\unicode[STIX]{x1D735}_{\!s}\boldsymbol{\cdot }\boldsymbol{u}_{s})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D707}_{s}[2K\boldsymbol{u}_{s}+\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}(\boldsymbol{n}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\!s}\times \boldsymbol{u}_{s})+2(\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}\boldsymbol{n}\times \boldsymbol{n})\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\!s}(\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n})]\nonumber\\ \displaystyle & & \displaystyle +\,\boldsymbol{n}[2H\unicode[STIX]{x1D70E}+2H(\unicode[STIX]{x1D707}_{d}+\unicode[STIX]{x1D707}_{s})\unicode[STIX]{x1D735}_{\!s}\boldsymbol{\cdot }\boldsymbol{u}_{s}-2\unicode[STIX]{x1D707}_{s}(\boldsymbol{n}\times \unicode[STIX]{x1D735}_{\!s}\boldsymbol{n}\times \boldsymbol{n})\boldsymbol{ : }\unicode[STIX]{x1D735}_{\!s}\boldsymbol{u}_{s}],\end{eqnarray}$$
where
are the mean and Gaussian curvatures of a surface respectively and
![]() $\unicode[STIX]{x1D70E}$
is the surface tension coefficient. Neglecting higher-order terms, the leading-order surface stress boundary condition in the context of small-amplitude capillary waves takes the reduced form
$\unicode[STIX]{x1D70E}$
is the surface tension coefficient. Neglecting higher-order terms, the leading-order surface stress boundary condition in the context of small-amplitude capillary waves takes the reduced form
where
![]() $\tilde{\unicode[STIX]{x1D70E}}$
is the surface tension augmented with the leading-order surface viscosity contribution given by
$\tilde{\unicode[STIX]{x1D70E}}$
is the surface tension augmented with the leading-order surface viscosity contribution given by
Using the equation of motion derived in § 3, the leading-order surface viscosity effect on the small-amplitude capillary wave can naturally be characterised (Lopez & Hirsa Reference Lopez and Hirsa1998) by the non-dimensional Boussinesq number
where
![]() $Bq_{d}=\unicode[STIX]{x1D707}_{d}k/\unicode[STIX]{x1D707}$
and
$Bq_{d}=\unicode[STIX]{x1D707}_{d}k/\unicode[STIX]{x1D707}$
and
![]() $Bq_{s}=\unicode[STIX]{x1D707}_{s}k/\unicode[STIX]{x1D707}$
are the Boussinesq dilatational and shear numbers respectively for dynamic viscosity
$Bq_{s}=\unicode[STIX]{x1D707}_{s}k/\unicode[STIX]{x1D707}$
are the Boussinesq dilatational and shear numbers respectively for dynamic viscosity
![]() $\unicode[STIX]{x1D707}$
and wavenumber
$\unicode[STIX]{x1D707}$
and wavenumber
![]() $k$
. More explicitly, surface viscosity can be modelled to be proportional to the surfactant concentration (Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017). In the case of detergents, experimental work by Brown, Thuman & McBain (Reference Brown, Thuman and McBain1953) suggests a bi-partisan action of the special solute pairs present in the detergent, where the primary constituent provides a large reservoir of surface-active material while the secondary constituent, lesser in amount, forms surface films of high viscosity. However, in the leading-order dynamics of the Boussinesq–Scriven formulation, surface viscosity is shown in § 3 to not depend explicitly on the surfactant concentration and enters only implicitly via the surface tension coefficient.
$k$
. More explicitly, surface viscosity can be modelled to be proportional to the surfactant concentration (Ponce-Torres et al.
Reference Ponce-Torres, Montanero, Herrada, Vega and Vega2017). In the case of detergents, experimental work by Brown, Thuman & McBain (Reference Brown, Thuman and McBain1953) suggests a bi-partisan action of the special solute pairs present in the detergent, where the primary constituent provides a large reservoir of surface-active material while the secondary constituent, lesser in amount, forms surface films of high viscosity. However, in the leading-order dynamics of the Boussinesq–Scriven formulation, surface viscosity is shown in § 3 to not depend explicitly on the surfactant concentration and enters only implicitly via the surface tension coefficient.
The other non-dimensional numbers of the system that arise naturally in the equation of motion are the viscosity (
![]() $\unicode[STIX]{x1D716}$
), surfactant diffusivity (
$\unicode[STIX]{x1D716}$
), surfactant diffusivity (
![]() $\unicode[STIX]{x1D70D}$
) and surfactant strength (
$\unicode[STIX]{x1D70D}$
) and surfactant strength (
![]() $\unicode[STIX]{x1D6FD}$
) parameters, given by
$\unicode[STIX]{x1D6FD}$
) parameters, given by
where
![]() $D_{s}$
denotes the coefficient of surface diffusivity,
$D_{s}$
denotes the coefficient of surface diffusivity,
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}$
is the kinematic viscosity for fluid density
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}$
is the kinematic viscosity for fluid density
![]() $\unicode[STIX]{x1D70C}$
,
$\unicode[STIX]{x1D70C}$
,
![]() $\unicode[STIX]{x1D6FC}=|\text{d}\unicode[STIX]{x1D70E}/\text{d}\unicode[STIX]{x1D6E4}|$
is the gradient of the surface tension coefficient,
$\unicode[STIX]{x1D6FC}=|\text{d}\unicode[STIX]{x1D70E}/\text{d}\unicode[STIX]{x1D6E4}|$
is the gradient of the surface tension coefficient,
![]() $\unicode[STIX]{x1D714}$
is the frequency of the capillary wave and
$\unicode[STIX]{x1D714}$
is the frequency of the capillary wave and
![]() $\unicode[STIX]{x1D6E4}_{0}$
is the initial surfactant concentration, which is assumed to be much less than the critical micelle concentration (cmc). In this system, these parameters act as the effective Reynolds, Schmidt and Marangoni numbers respectively.
$\unicode[STIX]{x1D6E4}_{0}$
is the initial surfactant concentration, which is assumed to be much less than the critical micelle concentration (cmc). In this system, these parameters act as the effective Reynolds, Schmidt and Marangoni numbers respectively.
3 Equations of motion
The dynamics of an incompressible fluid of viscosity
![]() $\unicode[STIX]{x1D707}$
and density
$\unicode[STIX]{x1D707}$
and density
![]() $\unicode[STIX]{x1D70C}$
in a region of Reynolds number
$\unicode[STIX]{x1D70C}$
in a region of Reynolds number
![]() $\mathit{Re}=U\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}\ll 1$
satisfies the Stokes equation
$\mathit{Re}=U\unicode[STIX]{x1D706}/\unicode[STIX]{x1D708}\ll 1$
satisfies the Stokes equation
where
![]() $\boldsymbol{u}=(u,v)$
is the two-dimensional fluid velocity field,
$\boldsymbol{u}=(u,v)$
is the two-dimensional fluid velocity field,
![]() $p$
is the pressure and
$p$
is the pressure and
![]() $\boldsymbol{F}=-g\,\boldsymbol{j}$
is the external (gravitational) force, with
$\boldsymbol{F}=-g\,\boldsymbol{j}$
is the external (gravitational) force, with
![]() $\boldsymbol{j}$
denoting the upward unit vector in the
$\boldsymbol{j}$
denoting the upward unit vector in the
![]() $y$
direction, and
$y$
direction, and
![]() $g$
is the gravitational acceleration. The small-amplitude capillary wave is given at the free surface
$g$
is the gravitational acceleration. The small-amplitude capillary wave is given at the free surface
![]() $F$
by the standing wave
$F$
by the standing wave
where
![]() $a(t)$
is the nonlinear time-dependent wave amplitude which satisfies the small-amplitude conditions that
$a(t)$
is the nonlinear time-dependent wave amplitude which satisfies the small-amplitude conditions that
![]() $a\ll \unicode[STIX]{x1D706}\,=2\unicode[STIX]{x03C0}/k$
and
$a\ll \unicode[STIX]{x1D706}\,=2\unicode[STIX]{x03C0}/k$
and
![]() $\text{d}a/\text{d}t\ll v_{c}=\unicode[STIX]{x1D714}/k$
, where
$\text{d}a/\text{d}t\ll v_{c}=\unicode[STIX]{x1D714}/k$
, where
![]() $\unicode[STIX]{x1D706}$
is the wavelength and
$\unicode[STIX]{x1D706}$
is the wavelength and
![]() $v_{c}$
is the phase velocity.
$v_{c}$
is the phase velocity.
For vanishing Gaussian curvature in a two-dimensional space, the leading-order tangential and normal stress components
![]() $T_{\Vert }$
and
$T_{\Vert }$
and
![]() $T_{\bot }$
and the kinematic condition are given by
$T_{\bot }$
and the kinematic condition are given by
respectively. The leading-order normal and tangent vectors are
Similarly to the small-amplitude condition, we consider a small departure from the equilibrium surface tension and let the coefficient of surface tension
![]() $\unicode[STIX]{x1D70E}$
be defined via a linear equation of state,
$\unicode[STIX]{x1D70E}$
be defined via a linear equation of state,
where
![]() $\unicode[STIX]{x1D70E}_{0}$
is the initial surface tension coefficient and
$\unicode[STIX]{x1D70E}_{0}$
is the initial surface tension coefficient and
![]() $\unicode[STIX]{x1D6E4}(x,t)$
is the (dilute) concentration of a surfactant solution where adsorptive–desorptive processes are neglected.
$\unicode[STIX]{x1D6E4}(x,t)$
is the (dilute) concentration of a surfactant solution where adsorptive–desorptive processes are neglected.
Using the waveform
![]() $\unicode[STIX]{x1D6E4}(x,t)-\unicode[STIX]{x1D6E4}_{0}=\tilde{\unicode[STIX]{x1D6E4}}(t)\cos kx,$
the governing equation for surfactant concentration along a two-dimensional deforming surface (Stone Reference Stone1990) is given by
$\unicode[STIX]{x1D6E4}(x,t)-\unicode[STIX]{x1D6E4}_{0}=\tilde{\unicode[STIX]{x1D6E4}}(t)\cos kx,$
the governing equation for surfactant concentration along a two-dimensional deforming surface (Stone Reference Stone1990) is given by
to the leading order,
![]() $\unicode[STIX]{x1D714}_{z}(x,y,t)=\unicode[STIX]{x1D6FA}(y,t)\sin kx$
is the
$\unicode[STIX]{x1D714}_{z}(x,y,t)=\unicode[STIX]{x1D6FA}(y,t)\sin kx$
is the
![]() $z$
component of the vorticity,
$z$
component of the vorticity,
![]() $\ast$
is the convolution operator and
$\ast$
is the convolution operator and
![]() ${\mathcal{F}}(t)$
is the auxiliary function
${\mathcal{F}}(t)$
is the auxiliary function
The fluid velocity and the pressure can be decomposed into the sum of an inviscid and a viscous part, i.e.
![]() $(\boldsymbol{u},p)=(\boldsymbol{u}^{\prime }+\boldsymbol{u}^{\prime \prime },\,p^{\prime }+p^{\prime \prime })$
. The inviscid part
$(\boldsymbol{u},p)=(\boldsymbol{u}^{\prime }+\boldsymbol{u}^{\prime \prime },\,p^{\prime }+p^{\prime \prime })$
. The inviscid part
![]() $(\boldsymbol{u}^{\prime },p^{\prime })$
satisfies the Euler problem
$(\boldsymbol{u}^{\prime },p^{\prime })$
satisfies the Euler problem
with well-known solutions (Lamb Reference Lamb1932)
where
![]() $\boldsymbol{u}^{\prime }=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
. The viscous component
$\boldsymbol{u}^{\prime }=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}$
. The viscous component
![]() $(\boldsymbol{u}^{\prime \prime },p^{\prime \prime })$
satisfies the Stokes problem
$(\boldsymbol{u}^{\prime \prime },p^{\prime \prime })$
satisfies the Stokes problem
which is solved by introducing the streamfunction
![]() $\unicode[STIX]{x1D713}$
, defined by
$\unicode[STIX]{x1D713}$
, defined by
![]() $\boldsymbol{u}^{\prime \prime }=(\unicode[STIX]{x1D713}_{y},-\unicode[STIX]{x1D713}_{x})$
. By taking the curl of (3.15), we obtain the bi-harmonic equation
$\boldsymbol{u}^{\prime \prime }=(\unicode[STIX]{x1D713}_{y},-\unicode[STIX]{x1D713}_{x})$
. By taking the curl of (3.15), we obtain the bi-harmonic equation
By writing
![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D6F9}(y,t)\sin kx$
, the Stokes problem yields the solution
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D6F9}(y,t)\sin kx$
, the Stokes problem yields the solution
where we have the viscous pressure correction
![]() $p^{\prime \prime }(x,y,t)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FA}(0,t)\text{e}^{ky}\cos kx$
and the boundary vorticity
$p^{\prime \prime }(x,y,t)=\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FA}(0,t)\text{e}^{ky}\cos kx$
and the boundary vorticity
Henceforth, using non-dimensional variables
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}t,$
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D714}t,$
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}k^{2}/\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D708}k^{2}/\unicode[STIX]{x1D714}$
and
![]() $\tilde{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FA}(0,t)/\unicode[STIX]{x1D714}$
, the boundary vorticity becomes the integral equation
$\tilde{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FA}(0,t)/\unicode[STIX]{x1D714}$
, the boundary vorticity becomes the integral equation
where we have
Here,
![]() $A=a/a_{0}$
is the dimensionless amplitude,
$A=a/a_{0}$
is the dimensionless amplitude,
![]() $\unicode[STIX]{x1D6FF}=a_{0}k$
and
$\unicode[STIX]{x1D6FF}=a_{0}k$
and
![]() $\dot{\,}=\text{d}/\text{d}\unicode[STIX]{x1D70F}$
denotes the non-dimensional temporal derivative. By substituting the pressure and the velocity into (3.5) and (3.10), we have the simultaneous equation
$\dot{\,}=\text{d}/\text{d}\unicode[STIX]{x1D70F}$
denotes the non-dimensional temporal derivative. By substituting the pressure and the velocity into (3.5) and (3.10), we have the simultaneous equation
Equations (3.23) and (3.24) provide us with a dynamic equation system for the amplitude and the surfactant concentration, the solution of which we outline in the next section.
4 Solution of the simultaneous integro-differential equation
Let
![]() $F(s)={\mathcal{L}}[A](s)$
,
$F(s)={\mathcal{L}}[A](s)$
,
![]() $G(s)={\mathcal{L}}[\tilde{\unicode[STIX]{x1D6E4}}](s)$
and
$G(s)={\mathcal{L}}[\tilde{\unicode[STIX]{x1D6E4}}](s)$
and
![]() $\hat{\unicode[STIX]{x1D6F1}}(s)=sF(s)-A_{0}$
be the Laplace transforms of
$\hat{\unicode[STIX]{x1D6F1}}(s)=sF(s)-A_{0}$
be the Laplace transforms of
![]() $A(\unicode[STIX]{x1D70F}),\,\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D70F})$
and
$A(\unicode[STIX]{x1D70F}),\,\tilde{\unicode[STIX]{x1D6E4}}(\unicode[STIX]{x1D70F})$
and
![]() ${\dot{A}}(\unicode[STIX]{x1D70F})$
, and define the polynomial expressions
${\dot{A}}(\unicode[STIX]{x1D70F})$
, and define the polynomial expressions
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D716}}^{(i)}\equiv \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D716}}^{(i)}(s+\unicode[STIX]{x1D716})$
for
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D716}}^{(i)}\equiv \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D716}}^{(i)}(s+\unicode[STIX]{x1D716})$
for
![]() $1\leqslant i\leqslant 6$
as
$1\leqslant i\leqslant 6$
as
where
![]() $B^{\prime }=1+B$
. The rational function
$B^{\prime }=1+B$
. The rational function
![]() $\hat{\unicode[STIX]{x1D6F1}}_{\unicode[STIX]{x1D716}}=\hat{\unicode[STIX]{x1D6F1}}_{\unicode[STIX]{x1D716}}(s+\unicode[STIX]{x1D716})=\text{P}(s^{1/2})/\text{Q}(s^{1/2})$
is decomposed into its partial fraction
$\hat{\unicode[STIX]{x1D6F1}}_{\unicode[STIX]{x1D716}}=\hat{\unicode[STIX]{x1D6F1}}_{\unicode[STIX]{x1D716}}(s+\unicode[STIX]{x1D716})=\text{P}(s^{1/2})/\text{Q}(s^{1/2})$
is decomposed into its partial fraction
where
![]() $-z_{i}$
are the roots of the polynomial
$-z_{i}$
are the roots of the polynomial
![]() $\text{Q}(s^{1/2})$
. In the absence of the Marangoni effect, the surface viscosity case is given by
$\text{Q}(s^{1/2})$
. In the absence of the Marangoni effect, the surface viscosity case is given by
By comparison with Lagrange polynomial interpolation, we have
where
![]() $\unicode[STIX]{x1D70E}_{i}^{(n)}$
is the
$\unicode[STIX]{x1D70E}_{i}^{(n)}$
is the
![]() $n$
th-order cyclic polynomial given by
$n$
th-order cyclic polynomial given by
It follows that by comparing (4.7) and (4.11), the coefficients
![]() $c_{i}$
are
$c_{i}$
are
![]() $c_{i}=\text{P}(-z_{i})/\unicode[STIX]{x1D70E}_{i}^{(10)}(-z_{i})$
. Let
$c_{i}=\text{P}(-z_{i})/\unicode[STIX]{x1D70E}_{i}^{(10)}(-z_{i})$
. Let
it follows (see appendix A) that the condition
implies
![]() $\text{Z}(n,0)=0$
, where
$\text{Z}(n,0)=0$
, where
![]() $\deg X$
is the degree of the polynomial
$\deg X$
is the degree of the polynomial
![]() $X$
. By taking the inverse Laplace transform of (4.8), we obtain
$X$
. By taking the inverse Laplace transform of (4.8), we obtain
Finally, the non-dimensional amplitude is given by
where
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(z_{i},\unicode[STIX]{x1D70F};\unicode[STIX]{x1D716})$
satisfies
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}(z_{i},\unicode[STIX]{x1D70F};\unicode[STIX]{x1D716})$
satisfies
5 Surface viscosity effects on the wave amplitude
As shown in § 4, the leading-order surface viscosity effects on the dynamics of small-amplitude capillary waves are characterised by the parameter
![]() $B$
, and, similarly, the Marangoni effect can be reduced to the non-dimensional variables
$B$
, and, similarly, the Marangoni effect can be reduced to the non-dimensional variables
![]() $\unicode[STIX]{x1D70D}$
and
$\unicode[STIX]{x1D70D}$
and
![]() $\unicode[STIX]{x1D6FD}$
given in § 2. In what follows, we use water under room temperature and pressure (rtp), i.e. at
$\unicode[STIX]{x1D6FD}$
given in § 2. In what follows, we use water under room temperature and pressure (rtp), i.e. at
![]() $25\,^{\circ }\text{C}$
, with density
$25\,^{\circ }\text{C}$
, with density
![]() $\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
, surface tension
$\unicode[STIX]{x1D70C}=10^{3}~\text{kg}~\text{m}^{-3}$
, surface tension
![]() $\unicode[STIX]{x1D70E}=7.2\times 10^{-2}~\text{N}~\text{m}^{-1}$
and viscosity
$\unicode[STIX]{x1D70E}=7.2\times 10^{-2}~\text{N}~\text{m}^{-1}$
and viscosity
![]() $\unicode[STIX]{x1D707}=8.9\times 10^{-4}~\text{Pa}~\text{s}$
, as a test system with surfactant Schmidt number
$\unicode[STIX]{x1D707}=8.9\times 10^{-4}~\text{Pa}~\text{s}$
, as a test system with surfactant Schmidt number
![]() $\mathit{Sc}=\unicode[STIX]{x1D708}/D_{s}=10^{4}$
. We define
$\mathit{Sc}=\unicode[STIX]{x1D708}/D_{s}=10^{4}$
. We define
![]() $\unicode[STIX]{x1D706}_{c}^{(0)}$
to be the wavelength for which the capillary wave undergoes critical damping, henceforth known as the critical wavelength. The superscript denotes the clean case, which we understand as a system without the addition of surface-active material, i.e.
$\unicode[STIX]{x1D706}_{c}^{(0)}$
to be the wavelength for which the capillary wave undergoes critical damping, henceforth known as the critical wavelength. The superscript denotes the clean case, which we understand as a system without the addition of surface-active material, i.e.
![]() $\unicode[STIX]{x1D6FD}=B=0$
. We will look at this critical wavelength in more detail in § 7, but here we note a harmonic oscillator approximation of
$\unicode[STIX]{x1D6FD}=B=0$
. We will look at this critical wavelength in more detail in § 7, but here we note a harmonic oscillator approximation of
![]() $\unicode[STIX]{x1D706}_{c}^{(0)}$
(Denner Reference Denner2016) whereby
$\unicode[STIX]{x1D706}_{c}^{(0)}$
(Denner Reference Denner2016) whereby
for
![]() $\unicode[STIX]{x1D6E9}=1.0625$
and the viscocapillary length scale
$\unicode[STIX]{x1D6E9}=1.0625$
and the viscocapillary length scale
In figure 1, we compare the effect of surface viscosity with that of the equivalent bulk viscosity
![]() $\unicode[STIX]{x1D708}$
, and the Marangoni effect with that of simple reductions in the surface tension coefficient
$\unicode[STIX]{x1D708}$
, and the Marangoni effect with that of simple reductions in the surface tension coefficient
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E4}_{0}$
. Here, we use the phrase equivalent to denote the quantities of bulk viscosity and simple reductions in surface tension that result in an identical effect on the overall wave amplitude due to surface viscosity and the Marangoni effect respectively under the limit of either a large or a small wavelength. For wavelengths near critical damping, in figure 1(a), an increase in
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E4}_{0}$
. Here, we use the phrase equivalent to denote the quantities of bulk viscosity and simple reductions in surface tension that result in an identical effect on the overall wave amplitude due to surface viscosity and the Marangoni effect respectively under the limit of either a large or a small wavelength. For wavelengths near critical damping, in figure 1(a), an increase in
![]() $B$
exhibits a relatively large difference from an equivalent increase in
$B$
exhibits a relatively large difference from an equivalent increase in
![]() $\unicode[STIX]{x1D708}$
, as compared with the case for
$\unicode[STIX]{x1D708}$
, as compared with the case for
![]() $\unicode[STIX]{x1D706}=950\unicode[STIX]{x1D706}_{c}^{(0)}$
in figure 1(d). This difference decreases as we increase the wavelength into less damped regions, as shown in figure 1(b,c). In contrast, the picture is reversed for the Marangoni effect, where equivalent changes in the surface tension coefficient are almost identical to increases in surfactant concentration (through
$\unicode[STIX]{x1D706}=950\unicode[STIX]{x1D706}_{c}^{(0)}$
in figure 1(d). This difference decreases as we increase the wavelength into less damped regions, as shown in figure 1(b,c). In contrast, the picture is reversed for the Marangoni effect, where equivalent changes in the surface tension coefficient are almost identical to increases in surfactant concentration (through
![]() $\unicode[STIX]{x1D6FD}$
) near critical damping in figure 1(e), and their difference increases with larger wavelength from figure 1(f) to 1(h), where the dynamic Marangoni effect vastly overshadows the static changes in the surface tension coefficient. Henceforth, we can approximate the Marangoni effect on the wave amplitude near the critical wavelength with the equivalent reduction in
$\unicode[STIX]{x1D6FD}$
) near critical damping in figure 1(e), and their difference increases with larger wavelength from figure 1(f) to 1(h), where the dynamic Marangoni effect vastly overshadows the static changes in the surface tension coefficient. Henceforth, we can approximate the Marangoni effect on the wave amplitude near the critical wavelength with the equivalent reduction in
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
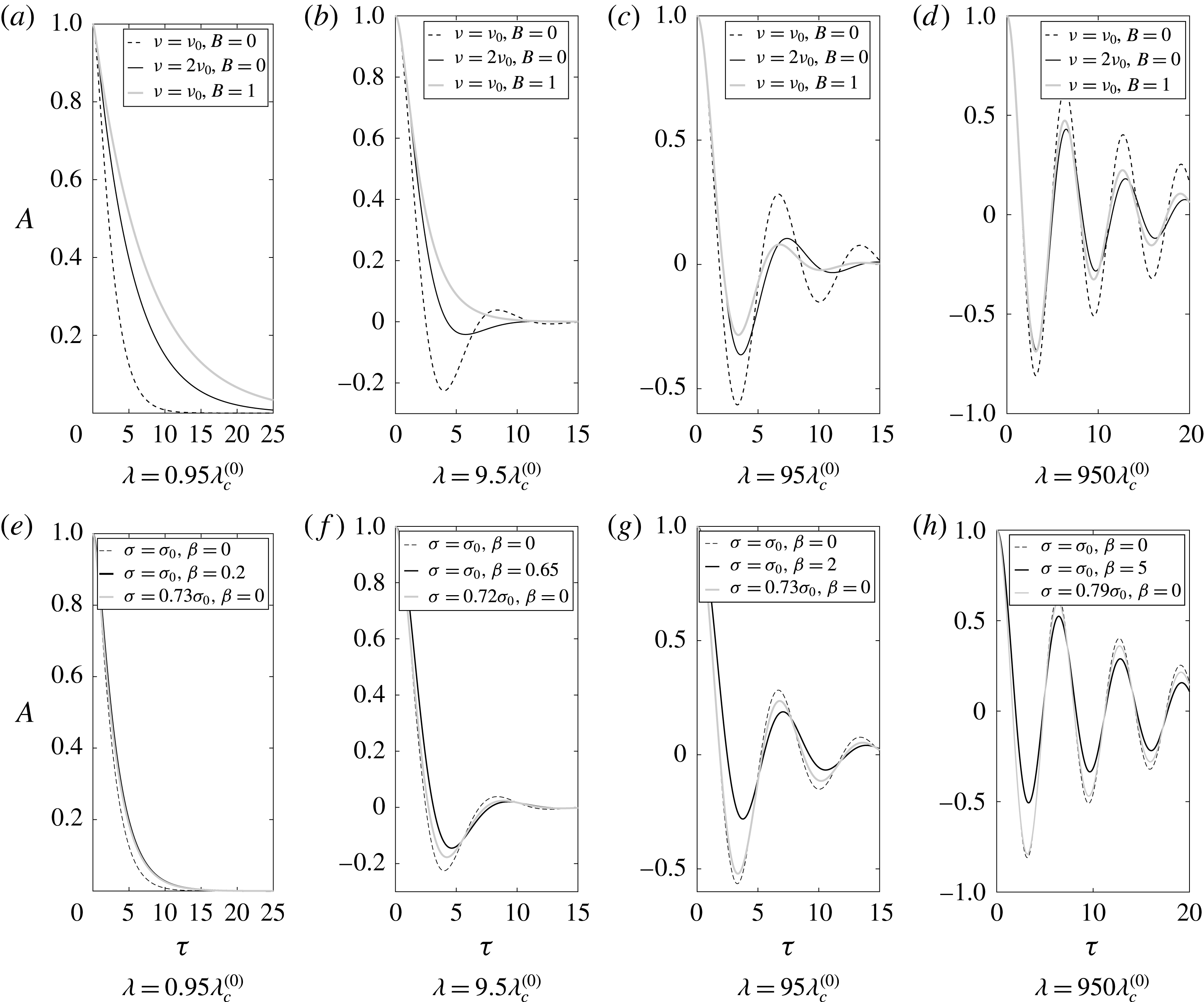
Figure 1. The wave amplitude as a function of the dimensionless time
![]() $\unicode[STIX]{x1D70F}$
for water at approximate room temperature and pressure for
$\unicode[STIX]{x1D70F}$
for water at approximate room temperature and pressure for
![]() $\mathit{Sc}=10^{4}$
, comparing the influence of the surface viscosity and Marangoni effects for various values of
$\mathit{Sc}=10^{4}$
, comparing the influence of the surface viscosity and Marangoni effects for various values of
![]() $B$
(with
$B$
(with
![]() $\unicode[STIX]{x1D6FD}=0$
) and
$\unicode[STIX]{x1D6FD}=0$
) and
![]() $\unicode[STIX]{x1D6FD}$
(with
$\unicode[STIX]{x1D6FD}$
(with
![]() $B=0$
). Here,
$B=0$
). Here,
![]() $\unicode[STIX]{x1D708}_{0}=8.9\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D708}_{0}=8.9\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
and
![]() $\unicode[STIX]{x1D70E}_{0}=0.072~\text{N}~\text{m}^{-1}$
denote the baseline kinematic viscosity and surface tension respectively. The modified surface tension in (e,f) represents a clean system (i.e.
$\unicode[STIX]{x1D70E}_{0}=0.072~\text{N}~\text{m}^{-1}$
denote the baseline kinematic viscosity and surface tension respectively. The modified surface tension in (e,f) represents a clean system (i.e.
![]() $\unicode[STIX]{x1D6FD}=B=0$
) with
$\unicode[STIX]{x1D6FD}=B=0$
) with
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E4}_{0}$
.
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{0}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E4}_{0}$
.
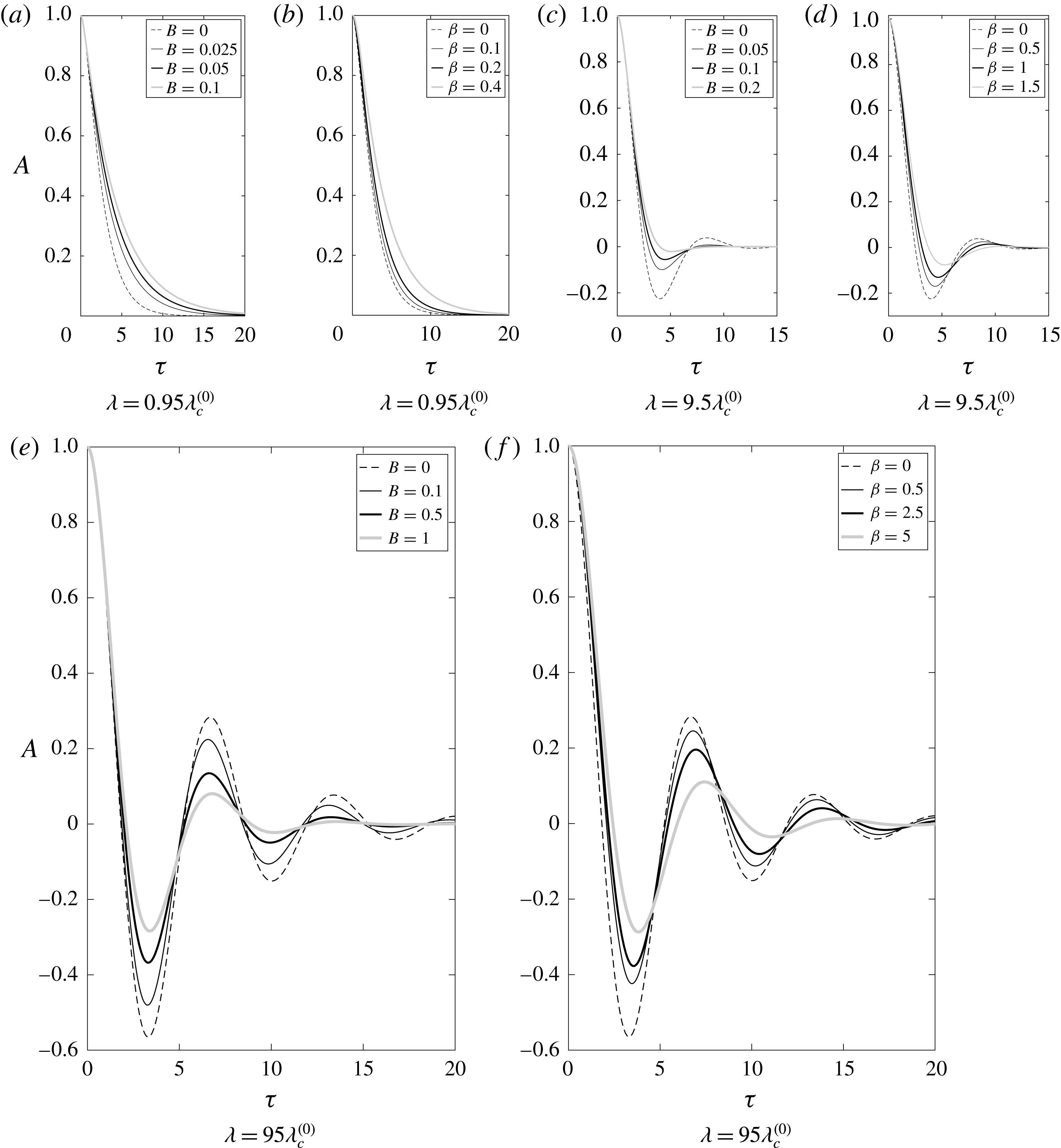
Figure 2. The wave amplitude as a function of the dimensionless time
![]() $\unicode[STIX]{x1D70F}$
for water at approximate room temperature and pressure for
$\unicode[STIX]{x1D70F}$
for water at approximate room temperature and pressure for
![]() $\mathit{Sc}=10^{4}$
, showing the influence of the surface viscosity and Marangoni effects for various values of
$\mathit{Sc}=10^{4}$
, showing the influence of the surface viscosity and Marangoni effects for various values of
![]() $B$
(with
$B$
(with
![]() $\unicode[STIX]{x1D6FD}=0$
) and
$\unicode[STIX]{x1D6FD}=0$
) and
![]() $\unicode[STIX]{x1D6FD}$
(with
$\unicode[STIX]{x1D6FD}$
(with
![]() $B=0$
) for different wavelengths
$B=0$
) for different wavelengths
![]() $\unicode[STIX]{x1D706}$
.
$\unicode[STIX]{x1D706}$
.
In figure 2, we see in more detail the mechanisms of surface viscosity and the Marangoni effect at different wave amplitudes for different wavelengths. Both effects admit relatively self-similar solutions, and on increasing either the surface viscosity or the surfactant concentration, the damping is increased, as expected. One of the explicit differences is that the Marangoni effect reduces the surface tension and, thus, lowers the frequency
![]() $\unicode[STIX]{x1D714}$
, while the surface viscosity leaves
$\unicode[STIX]{x1D714}$
, while the surface viscosity leaves
![]() $\unicode[STIX]{x1D714}$
unchanged. This is due to the surface viscosity being dependent on the surfactant concentration only to the linear order, and it does not feature in the leading-order nonlinear amplitude equation (3.23) explicitly, as noted previously. The consequence on the amplitude of this
$\unicode[STIX]{x1D714}$
unchanged. This is due to the surface viscosity being dependent on the surfactant concentration only to the linear order, and it does not feature in the leading-order nonlinear amplitude equation (3.23) explicitly, as noted previously. The consequence on the amplitude of this
![]() $\unicode[STIX]{x1D714}$
lowering is a horizontal drift of the waveform for systems with the Marangoni effect, as is evident from figure 2(d,f), as opposed to relatively centred waveforms in the cases of surface viscosity in figure 2(c,e).
$\unicode[STIX]{x1D714}$
lowering is a horizontal drift of the waveform for systems with the Marangoni effect, as is evident from figure 2(d,f), as opposed to relatively centred waveforms in the cases of surface viscosity in figure 2(c,e).
We also observe that the surface viscosity effect weakens for large wavelengths
![]() $\unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D706}_{c}$
but is very potent for small wavelengths
$\unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D706}_{c}$
but is very potent for small wavelengths
![]() $\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D706}_{c}$
. A particular consequence of this potency is its ability to alter the onset behaviour in interfacial phenomena, a number of which occur near the region of the critical wavelength. The stochastic nature of many of the interfacial instabilities (Aarts et al.
Reference Aarts, Schmidt and Lekkerkerker2004) is often kickstarted by the small-amplitude local disturbances on the interface. Hence, a small change in surface material, and thus the wave damping, can have a significant effect in starting or delaying the initialisation process of more complex phenomena. Furthermore, it would be of interest to obtain the modification to the critical wavelength upon the addition of a small amount surface-active material. However, we need to consider the definition of the critical wavelength for a higher-order system as it is not as readily defined as in a second-order system.
$\unicode[STIX]{x1D706}\sim \unicode[STIX]{x1D706}_{c}$
. A particular consequence of this potency is its ability to alter the onset behaviour in interfacial phenomena, a number of which occur near the region of the critical wavelength. The stochastic nature of many of the interfacial instabilities (Aarts et al.
Reference Aarts, Schmidt and Lekkerkerker2004) is often kickstarted by the small-amplitude local disturbances on the interface. Hence, a small change in surface material, and thus the wave damping, can have a significant effect in starting or delaying the initialisation process of more complex phenomena. Furthermore, it would be of interest to obtain the modification to the critical wavelength upon the addition of a small amount surface-active material. However, we need to consider the definition of the critical wavelength for a higher-order system as it is not as readily defined as in a second-order system.
6 Capillary wave dispersion and the critical wavelength
To quantify the changes to the critical wavelength due to the presence of the Marangoni and surface viscosity effects, we must first obtain the critical wavelength in the clean case. Following Lamb (Reference Lamb1932), the general dispersion relation for an interface with both the Marangoni effect and surface viscosity can be found (derivation in appendix B) to take the form
where
and
On specialising to the clean case, (6.1) reduces to
as derived from linearised hydrodynamics (Lamb Reference Lamb1932; Levich Reference Levich1962). The dispersion relation admits a solution of the form
where
![]() $h^{2}=(1/3)-J_{+}^{1/3}-J_{-}^{1/3}$
for
$h^{2}=(1/3)-J_{+}^{1/3}-J_{-}^{1/3}$
for
where the polynomial
![]() $\text{f}(\unicode[STIX]{x1D716})$
is given by
$\text{f}(\unicode[STIX]{x1D716})$
is given by
For
![]() $\unicode[STIX]{x1D716}\ll \unicode[STIX]{x1D716}^{\star },$
the wave frequency can be written as
$\unicode[STIX]{x1D716}\ll \unicode[STIX]{x1D716}^{\star },$
the wave frequency can be written as
and the damping coefficient can be extracted as
![]() $\text{Im}(\unicode[STIX]{x1D714}^{\prime })\sim 2\unicode[STIX]{x1D716},$
where
$\text{Im}(\unicode[STIX]{x1D714}^{\prime })\sim 2\unicode[STIX]{x1D716},$
where
![]() $\unicode[STIX]{x1D716}^{\star }\in \mathbb{R}^{+}$
is the transition value defined by the (largest positive) root of the polynomial
$\unicode[STIX]{x1D716}^{\star }\in \mathbb{R}^{+}$
is the transition value defined by the (largest positive) root of the polynomial
![]() $\text{f},$
i.e.
$\text{f},$
i.e.
By solving (6.7) exactly, we obtain
with the numerical value
![]() $\unicode[STIX]{x1D716}^{\star }\simeq 1.3115.$
Reintroducing dimensional variables, we define
$\unicode[STIX]{x1D716}^{\star }\simeq 1.3115.$
Reintroducing dimensional variables, we define
![]() $P,Q$
and the variable
$P,Q$
and the variable
![]() $K$
by
$K$
by
It follows from the definition of
![]() $\unicode[STIX]{x1D716}$
that the critical wavenumber
$\unicode[STIX]{x1D716}$
that the critical wavenumber
![]() $k^{\star }$
satisfies the cubic equation
$k^{\star }$
satisfies the cubic equation
We require the real solution given by
where
By inspecting (6.15), the critical wavenumber under the limit
![]() $k\ll (\unicode[STIX]{x1D70C}\text{g}/\unicode[STIX]{x1D70E})^{1/2}$
is
$k\ll (\unicode[STIX]{x1D70C}\text{g}/\unicode[STIX]{x1D70E})^{1/2}$
is
![]() $k^{\star }\sim (\text{g}\unicode[STIX]{x1D716}^{\star 2}/\unicode[STIX]{x1D708}^{2})^{1/3},$
corresponding to the gravity-dominated regime with
$k^{\star }\sim (\text{g}\unicode[STIX]{x1D716}^{\star 2}/\unicode[STIX]{x1D708}^{2})^{1/3},$
corresponding to the gravity-dominated regime with
![]() $\unicode[STIX]{x1D714}_{0}\sim (\text{g}k)^{1/2}$
. For
$\unicode[STIX]{x1D714}_{0}\sim (\text{g}k)^{1/2}$
. For
![]() $k\geqslant (\unicode[STIX]{x1D70C}\text{g}/\unicode[STIX]{x1D70E})^{1/2}$
, the critical wavenumber reduces to
$k\geqslant (\unicode[STIX]{x1D70C}\text{g}/\unicode[STIX]{x1D70E})^{1/2}$
, the critical wavenumber reduces to
corresponding to the capillary-dominated regime with
![]() $\unicode[STIX]{x1D714}_{0}\sim (\unicode[STIX]{x1D70E}k^{3}/\unicode[STIX]{x1D70C})^{1/2}$
.
$\unicode[STIX]{x1D714}_{0}\sim (\unicode[STIX]{x1D70E}k^{3}/\unicode[STIX]{x1D70C})^{1/2}$
.
For
![]() $\unicode[STIX]{x1D716}\gg \unicode[STIX]{x1D716}^{\star }$
, we note that
$\unicode[STIX]{x1D716}\gg \unicode[STIX]{x1D716}^{\star }$
, we note that
![]() $\mathit{Re}(\unicode[STIX]{x1D714}^{\prime })=0$
and the system is in an overall overdamped regime. The damping ratio is given by expanding
$\mathit{Re}(\unicode[STIX]{x1D714}^{\prime })=0$
and the system is in an overall overdamped regime. The damping ratio is given by expanding
![]() $\unicode[STIX]{x1D714}_{-}^{\prime }$
(since
$\unicode[STIX]{x1D714}_{-}^{\prime }$
(since
![]() $\unicode[STIX]{x1D714}_{+}^{\prime }\gg \unicode[STIX]{x1D714}_{-}^{\prime }$
and would thus rapidly damp the motion) in (6.5) in ascending powers of
$\unicode[STIX]{x1D714}_{+}^{\prime }\gg \unicode[STIX]{x1D714}_{-}^{\prime }$
and would thus rapidly damp the motion) in (6.5) in ascending powers of
![]() $\unicode[STIX]{x1D716}^{-1}$
, i.e.
$\unicode[STIX]{x1D716}^{-1}$
, i.e.
This agrees with the asymptotic approximations by Levich (Reference Levich1962), which suggests that an increase of viscosity would decrease the damping for
![]() $\unicode[STIX]{x1D716}\gg \unicode[STIX]{x1D716}^{\star }$
.
$\unicode[STIX]{x1D716}\gg \unicode[STIX]{x1D716}^{\star }$
.
Using (6.18), the analytical critical wavelength (the value of
![]() $\unicode[STIX]{x1D706}$
with associated damping ratio
$\unicode[STIX]{x1D706}$
with associated damping ratio
![]() $\unicode[STIX]{x1D701}=1$
) of the capillary wave is given by
$\unicode[STIX]{x1D701}=1$
) of the capillary wave is given by
For water under rtp, we have
![]() $\unicode[STIX]{x1D706}_{c}^{\star }\doteq 40.1894~\text{nm}$
. In comparison, a harmonic oscillator approximation (Denner Reference Denner2016) in (5.1) gives the result
$\unicode[STIX]{x1D706}_{c}^{\star }\doteq 40.1894~\text{nm}$
. In comparison, a harmonic oscillator approximation (Denner Reference Denner2016) in (5.1) gives the result
![]() $\unicode[STIX]{x1D706}_{c}^{(0)}\doteq 40.9838~\text{nm}$
. We consider the relative error between the harmonic oscillator and the analytical critical wavelengths,
$\unicode[STIX]{x1D706}_{c}^{(0)}\doteq 40.9838~\text{nm}$
. We consider the relative error between the harmonic oscillator and the analytical critical wavelengths,
We observe that the system is largely second-order in the neighbourhood of the critical wavelength, as the harmonic oscillator value of
![]() $\unicode[STIX]{x1D706}_{c}$
is within 2 % of the analytical value from the wave dispersion.
$\unicode[STIX]{x1D706}_{c}$
is within 2 % of the analytical value from the wave dispersion.
7 Damping ratio for a generalised system
For systems of a higher order, the damping ratio
![]() $\unicode[STIX]{x1D701}$
is not naturally defined and we usually inspect the root-locus diagram in order to decompose the system into a sum of first- and second-ordered systems to provide an estimate calculation. Here, we consider a numerical method to obtain an equivalent damping ratio, whereby
$\unicode[STIX]{x1D701}$
is not naturally defined and we usually inspect the root-locus diagram in order to decompose the system into a sum of first- and second-ordered systems to provide an estimate calculation. Here, we consider a numerical method to obtain an equivalent damping ratio, whereby
![]() $\unicode[STIX]{x1D701}\geqslant 1$
when the area of the amplitude below the settling value vanishes for all time almost everywhere. The critical wavelength is then the supremum of the set of wavelengths such that the above property holds. We express this as
$\unicode[STIX]{x1D701}\geqslant 1$
when the area of the amplitude below the settling value vanishes for all time almost everywhere. The critical wavelength is then the supremum of the set of wavelengths such that the above property holds. We express this as
where
![]() $H(x)$
is the Heaviside step function.
$H(x)$
is the Heaviside step function.
For underdamped waves, even for second-order systems, logarithmic decrement or fractional overshoot methods tend to break down or become less accurate near regions of critical damping. Hence, to determine the damping ratios in the neighbourhood of
![]() $\unicode[STIX]{x1D701}\approx 1$
, we adapt the area method in (7.1). We consider that the area under the
$\unicode[STIX]{x1D701}\approx 1$
, we adapt the area method in (7.1). We consider that the area under the
![]() $t$
-axis is given by the function
$t$
-axis is given by the function
where
![]() $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D701},t)$
satisfies the normalised harmonic oscillator equation
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D701},t)$
satisfies the normalised harmonic oscillator equation
The generalised (numerical) damping ratio for
![]() $\unicode[STIX]{x1D701}\leqslant 1$
can then be obtained by the inverse operation
$\unicode[STIX]{x1D701}\leqslant 1$
can then be obtained by the inverse operation
where
![]() $X$
is the area under the
$X$
is the area under the
![]() $t$
-axis of a generalised system. This numerical method agrees well with logarithmic decrement and fractional overshoot schemes in the relevant underdamped regimes.
$t$
-axis of a generalised system. This numerical method agrees well with logarithmic decrement and fractional overshoot schemes in the relevant underdamped regimes.
In cases where the higher-order system can readily be approximated locally by a second-order system, we note that its dominant poles have a larger residue and time constant
![]() $t_{c}=1/(\unicode[STIX]{x1D701}_{n}\unicode[STIX]{x1D714}_{n})$
relative to other poles, where
$t_{c}=1/(\unicode[STIX]{x1D701}_{n}\unicode[STIX]{x1D714}_{n})$
relative to other poles, where
![]() $\unicode[STIX]{x1D701}_{n}$
and
$\unicode[STIX]{x1D701}_{n}$
and
![]() $\unicode[STIX]{x1D714}_{n}$
are the damping ratio and frequency associated with each pole. In cases that are not clear cut, i.e. where all the poles are closer together with
$\unicode[STIX]{x1D714}_{n}$
are the damping ratio and frequency associated with each pole. In cases that are not clear cut, i.e. where all the poles are closer together with
![]() $t_{c}$
and residues of a similar magnitude, the numerical definition of the damping ratio above only provides an estimate of the true damping ratio and we need to examine the poles in more detail.
$t_{c}$
and residues of a similar magnitude, the numerical definition of the damping ratio above only provides an estimate of the true damping ratio and we need to examine the poles in more detail.
To encode such information into a convenient form, we construct the minimal pole matrix
![]() $\{\unicode[STIX]{x1D701}(\unicode[STIX]{x1D706})\}$
. To decompose the system, we first consider the minimal realisation of the transfer function. For a general system, let
$\{\unicode[STIX]{x1D701}(\unicode[STIX]{x1D706})\}$
. To decompose the system, we first consider the minimal realisation of the transfer function. For a general system, let
![]() $\unicode[STIX]{x1D6E9}_{1}=\{q_{i}\in \mathbb{C}:~\text{Q}(-q_{i})=0\}$
and
$\unicode[STIX]{x1D6E9}_{1}=\{q_{i}\in \mathbb{C}:~\text{Q}(-q_{i})=0\}$
and
![]() $\unicode[STIX]{x1D6E9}_{2}=\{p_{j}\in \mathbb{C}:\text{P}(-p_{j})=0\}$
be the sets of poles and zeros of the transfer function
$\unicode[STIX]{x1D6E9}_{2}=\{p_{j}\in \mathbb{C}:\text{P}(-p_{j})=0\}$
be the sets of poles and zeros of the transfer function
![]() $\text{tf}(s)\equiv \text{P}(s)/\text{Q}(s)$
, which can be written in the form
$\text{tf}(s)\equiv \text{P}(s)/\text{Q}(s)$
, which can be written in the form
By applying the pole-zero cancellation procedure, we obtain the minimal realisation of the transfer function, henceforth known as the minimal transfer function
![]() $\text{mtf}(s)$
, defined by
$\text{mtf}(s)$
, defined by
where the polynomials
![]() $\text{P}_{m}(s)$
and
$\text{P}_{m}(s)$
and
![]() $\text{Q}_{m}(s)$
satisfy
$\text{Q}_{m}(s)$
satisfy
and
![]() $\unicode[STIX]{x1D6E9}_{1,m}(\unicode[STIX]{x1D717})\subseteq \unicode[STIX]{x1D6E9}_{1}$
is the set of poles of
$\unicode[STIX]{x1D6E9}_{1,m}(\unicode[STIX]{x1D717})\subseteq \unicode[STIX]{x1D6E9}_{1}$
is the set of poles of
![]() $\text{Q}$
with significant residues (tolerance of order
$\text{Q}$
with significant residues (tolerance of order
![]() $\unicode[STIX]{x1D717}$
),
$\unicode[STIX]{x1D717}$
),
Returning to the construction of the minimal pole matrix, we let the first column of the matrix illustrate the order of the poles of the minimal transfer function in dot form; the second column considers the relative magnitudes of their time constant
![]() $t_{c}$
; the third column compares their relative residues; the fourth column gives the damping ratios
$t_{c}$
; the third column compares their relative residues; the fourth column gives the damping ratios
![]() $\unicode[STIX]{x1D701}_{n}$
associated with each pole. Furthermore, to the right of the line separator, we provide an estimated equivalent second-order damping ratio of the entire system using the area numerical method described previously. We say that a system is second-order dominant if one set of complex conjugate poles dominates the other poles (i.e. having the largest
$\unicode[STIX]{x1D701}_{n}$
associated with each pole. Furthermore, to the right of the line separator, we provide an estimated equivalent second-order damping ratio of the entire system using the area numerical method described previously. We say that a system is second-order dominant if one set of complex conjugate poles dominates the other poles (i.e. having the largest
![]() $t_{c}$
and residue). In diagrammatic form for
$t_{c}$
and residue). In diagrammatic form for
![]() $\unicode[STIX]{x1D717}=1$
, we have
$\unicode[STIX]{x1D717}=1$
, we have

For example, for
![]() $\unicode[STIX]{x1D706}=6.22\unicode[STIX]{x1D706}_{c}^{\star }$
at rtp, the clean case for water exhibits the following minimal pole matrix:
$\unicode[STIX]{x1D706}=6.22\unicode[STIX]{x1D706}_{c}^{\star }$
at rtp, the clean case for water exhibits the following minimal pole matrix:
from which we observe that the system is second-order dominant since the set of complex conjugate poles with associated damping ratio 0.45 dominates (in the sense of residue) the other, and, thus, we can deduce that the true damping ratio of the system is close to the approximate second-order value.
We take this analysis to the region near critical damping, i.e. for
![]() $\unicode[STIX]{x1D701}\rightarrow 1^{+}$
and
$\unicode[STIX]{x1D701}\rightarrow 1^{+}$
and
![]() $\unicode[STIX]{x1D701}\rightarrow 1^{-}$
. In the clean case, we take the analytical result
$\unicode[STIX]{x1D701}\rightarrow 1^{-}$
. In the clean case, we take the analytical result
![]() $\unicode[STIX]{x1D706}_{c}^{\star }=2\unicode[STIX]{x03C0}l_{vc}/\unicode[STIX]{x1D716}^{\star 2}$
to be the definition of the critical (damping) wavelength. The relevant minimal pole matrices take the form
$\unicode[STIX]{x1D706}_{c}^{\star }=2\unicode[STIX]{x03C0}l_{vc}/\unicode[STIX]{x1D716}^{\star 2}$
to be the definition of the critical (damping) wavelength. The relevant minimal pole matrices take the form
We can see that this transition from
![]() $\unicode[STIX]{x1D706}_{c}^{\star +}\rightarrow \unicode[STIX]{x1D706}_{c}^{\star -}$
for the clean case boasts a transformation of the complex conjugate into two separate first-order poles, or, in diagrammatic form, we have
$\unicode[STIX]{x1D706}_{c}^{\star +}\rightarrow \unicode[STIX]{x1D706}_{c}^{\star -}$
for the clean case boasts a transformation of the complex conjugate into two separate first-order poles, or, in diagrammatic form, we have
i.e. a
![]() $2^{2}$
–
$2^{2}$
–
![]() $1^{2}$
transition.
$1^{2}$
transition.
Extending to contaminated systems, we summarise the results of the minimal pole matrices of the system at the critical transition in table 1, where the notation
![]() $1^{a}2^{b}$
denotes a system with
$1^{a}2^{b}$
denotes a system with
![]() $a$
first-order and
$a$
first-order and
![]() $b$
second-order poles with significant relative residue. We note that the effect of surface viscosity is to introduce an extra first-order pole (with unit damping ratio) to the system, while the Marangoni effect does not change the pole composition for the underdamped region before the critical damping transition. Moreover, we observe at this critical damping transition that the system enters the overdamped regime if its minimal pole matrix is of the
$b$
second-order poles with significant relative residue. We note that the effect of surface viscosity is to introduce an extra first-order pole (with unit damping ratio) to the system, while the Marangoni effect does not change the pole composition for the underdamped region before the critical damping transition. Moreover, we observe at this critical damping transition that the system enters the overdamped regime if its minimal pole matrix is of the
![]() $1^{2}$
type irrespective of its type in the underdamped regime prior to the transition. Henceforth, we shall define a generalised higher-order (capillary) wave to be in overall overdamped motion if its minimal pole matrix is of the
$1^{2}$
type irrespective of its type in the underdamped regime prior to the transition. Henceforth, we shall define a generalised higher-order (capillary) wave to be in overall overdamped motion if its minimal pole matrix is of the
![]() $1^{2}$
type.
$1^{2}$
type.
Table 1. Schematic of poles at the transition from
![]() $\unicode[STIX]{x1D706}_{c}^{\star +}\rightarrow \unicode[STIX]{x1D706}_{c}^{\star -}$
for water at room temperature and pressure.
$\unicode[STIX]{x1D706}_{c}^{\star +}\rightarrow \unicode[STIX]{x1D706}_{c}^{\star -}$
for water at room temperature and pressure.
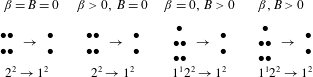
Using the definition of the overdamped regime for a generalised higher-order system, we determine numerically the corrections to the critical wavelength for increasing surface viscosity (through
![]() $B$
), surfactant concentration (through
$B$
), surfactant concentration (through
![]() $\unicode[STIX]{x1D6FD}$
) and bulk viscosity (through
$\unicode[STIX]{x1D6FD}$
) and bulk viscosity (through
![]() $\unicode[STIX]{x1D703}$
, where
$\unicode[STIX]{x1D703}$
, where
in figure 3). We note that the curves denoting surface viscosity and the Marangoni effect intersect near
![]() $B\simeq 0.65$
and that while the Marangoni curve is roughly exponential, the surface viscosity curve is the sum of two exponential functions. Moreover, we observe that a small amount of surface viscosity present in the system has an amplified effect on the system and that a sevenfold increase in critical wavelength for
$B\simeq 0.65$
and that while the Marangoni curve is roughly exponential, the surface viscosity curve is the sum of two exponential functions. Moreover, we observe that a small amount of surface viscosity present in the system has an amplified effect on the system and that a sevenfold increase in critical wavelength for
![]() $B=1$
results in very different dynamics and mechanisms as the sub-100 nm brings forward the possibility of long-range molecular interactions as well as the hydrodynamics. Also of consideration is the proximity of the critical wavelength to the wavelengths of the visible spectrum of light, which allows thin-film behaviours to be captured by light scattering methods. Hence, the presence of surfactants could determine whether or not we would be within such a range as to allow interferometry techniques.
$B=1$
results in very different dynamics and mechanisms as the sub-100 nm brings forward the possibility of long-range molecular interactions as well as the hydrodynamics. Also of consideration is the proximity of the critical wavelength to the wavelengths of the visible spectrum of light, which allows thin-film behaviours to be captured by light scattering methods. Hence, the presence of surfactants could determine whether or not we would be within such a range as to allow interferometry techniques.
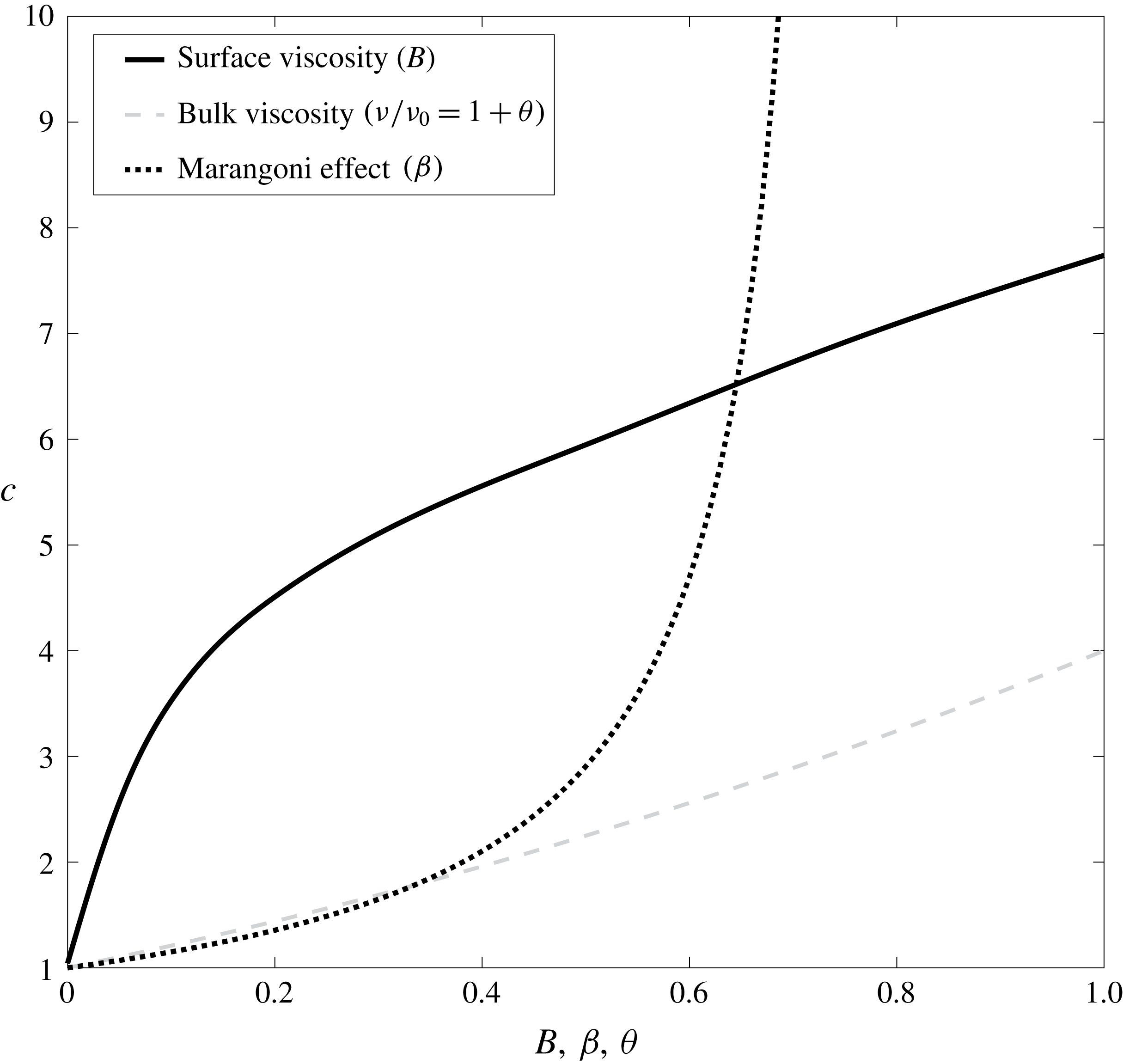
Figure 3. Independent corrections to the critical wavelength for increasing surface viscosity (via
![]() $B$
, with
$B$
, with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FD}=0$
), bulk viscosity (via
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FD}=0$
), bulk viscosity (via
![]() $\unicode[STIX]{x1D703}$
, where
$\unicode[STIX]{x1D703}$
, where
![]() $\unicode[STIX]{x1D708}/\unicode[STIX]{x1D708}_{0}=1+\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D708}/\unicode[STIX]{x1D708}_{0}=1+\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D6FD}=B=0$
) and Marangoni effect (through
$\unicode[STIX]{x1D6FD}=B=0$
) and Marangoni effect (through
![]() $\unicode[STIX]{x1D6FD}$
, with
$\unicode[STIX]{x1D6FD}$
, with
![]() $\unicode[STIX]{x1D703}=B=0$
).
$\unicode[STIX]{x1D703}=B=0$
).
Comparisons of the range with experimental and computational results on surface viscosity can be made using values reported previously in the literature. Experimentally, Kanner & Glass (Reference Kanner and Glass1969) summarised in table 2 the surface viscosities for both surfactant and polymeric films, where, for a dilute amount of sodium lauryl sulphate and polydimethylsiloxane in particular, the surface viscosity corresponds to a lower bound of
![]() $B=O(1)$
for
$B=O(1)$
for
![]() $k=O(10^{6})$
. A similar correspondence can be found with the upper bound surface shear viscosity of
$k=O(10^{6})$
. A similar correspondence can be found with the upper bound surface shear viscosity of
![]() $O(10^{-8}~\text{N}~\text{s}~\text{m}^{-1})$
found in Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) for soluble surfactants. We note that this measurement does not include surface dilatational viscosity and so corresponds to the case (Lucassen & Hansen Reference Lucassen and Hansen1966) where diffusional transport between the surface and the bulk is neglected, and assumes that the bulk viscosity and density are constant right up to the interface. More recently, Gounley et al. (Reference Gounley, Boedec, Jaeger and Leonetti2016) characterised the influence of both shear and dilatational surface viscosity on droplets in shear flow in the range
$O(10^{-8}~\text{N}~\text{s}~\text{m}^{-1})$
found in Zell et al. (Reference Zell, Nowbahar, Mansard, Leal, Deshmukh, Mecca, Tucker and Squires2014) for soluble surfactants. We note that this measurement does not include surface dilatational viscosity and so corresponds to the case (Lucassen & Hansen Reference Lucassen and Hansen1966) where diffusional transport between the surface and the bulk is neglected, and assumes that the bulk viscosity and density are constant right up to the interface. More recently, Gounley et al. (Reference Gounley, Boedec, Jaeger and Leonetti2016) characterised the influence of both shear and dilatational surface viscosity on droplets in shear flow in the range
![]() $B=O(10^{0})$
–
$B=O(10^{0})$
–
![]() $O(10^{1})$
for a range of capillary numbers.
$O(10^{1})$
for a range of capillary numbers.
Beyond the cmc value, the Marangoni effect should in principle have no overall contribution to the capillary wave; the dotted curve in figure 3 would end abruptly at the cmc value. The combination of surface viscosity together with the Marangoni effect is, however, not straightforward; as in previous experimental studies (Brown et al.
Reference Brown, Thuman and McBain1953; Kanner & Glass Reference Kanner and Glass1969), surface viscosity also appears to alter the ability of the Marangoni effect to lower surface tension. It would therefore be fruitful in a future contribution to investigate this surfactant interference mechanism through a more systematic experimental and theoretical study. In particular, a numerical approach similar to that of Sinclair, Levy & Daniels (Reference Sinclair, Levy and Daniels2018) could include the use of a nonlinear equation of state for the surface tension coefficient
![]() $\unicode[STIX]{x1D70E}$
. The effect of the deviation from the linear equation of state on the amplitude of the capillary wave would aid the analysis near the cmc value of the surfactant solution.
$\unicode[STIX]{x1D70E}$
. The effect of the deviation from the linear equation of state on the amplitude of the capillary wave would aid the analysis near the cmc value of the surfactant solution.
8 Conclusion
In this work, the surface viscosity effect has been incorporated into the integro-differential initial value problem describing the wave dynamics of small-amplitude capillary waves via the Boussinesq–Scriven surface model. We have shown that, particularly at length scales close to the critical damping wavelength, a very small amount of surface viscosity can dramatically increase the critical wavelength of the capillary waves, in contrast to the Marangoni effect which becomes prominent at larger wavelengths. In view of the important role that capillary waves play in inducing the rupture process of thin films (Aarts et al. Reference Aarts, Schmidt and Lekkerkerker2004), we anticipate the various interfacial phenomena controlling the wave dynamics at the very minute length scale to contribute towards the understanding of the stability of foams with non-trivial surface viscosity. In particular, the correction of the critical wavelength due to surface viscosity and Marangoni effects, which we summarised in figure 3 using numerical methods, is bound to alter the onset of fluid instabilities for very thin liquid films. It is also useful towards the optimisation of additives to achieve desired increases in the critical wavelength. Finally, we expect the concept of a critical damping wavelength and its correction by surface material to be useful for a further number of general interfacial phenomena, such as the onset of thin-film quasi-elastic wrinkling and Faraday-like instabilities in the same length scale.
Acknowledgements
The authors acknowledge the financial support of the Shell University Technology Centre for fuels and lubricants and the Engineering and Physical Sciences Research Council (EPSRC) through grants EP/M021556/1 and EP/N025954/1.
Appendix A. The condition
 $\deg \text{Q}-\deg \text{P}\geqslant 2\,\Rightarrow \,\text{Z}(n,0)=0$
$\deg \text{Q}-\deg \text{P}\geqslant 2\,\Rightarrow \,\text{Z}(n,0)=0$
We consider the rational expression
where
![]() $\text{P}(s,m)$
is a polynomial of order
$\text{P}(s,m)$
is a polynomial of order
![]() $m$
in
$m$
in
![]() $s$
,
$s$
,
is a polynomial of order
![]() $n>m$
in
$n>m$
in
![]() $s$
with distinct roots
$s$
with distinct roots
![]() $q_{i}$
and
$q_{i}$
and
On rewriting
![]() $\hat{\text{f}}(s)$
using a partial fraction decomposition, we have
$\hat{\text{f}}(s)$
using a partial fraction decomposition, we have
and by taking an inverse Laplace transform, we obtain
where
![]() $q_{i}$
are roots of the polynomial
$q_{i}$
are roots of the polynomial
![]() $\text{Q}(s,n)$
and
$\text{Q}(s,n)$
and
Expansion of (A 2) for large
![]() $s$
and inversion termwise gives
$s$
and inversion termwise gives
Comparison with (A 8) shows that
![]() $\text{Z}(n,j)=0$
if
$\text{Z}(n,j)=0$
if
which reduces to the condition
Appendix B. The contaminated wave dispersion relation
Following Lamb (Reference Lamb1932) and using the equations of motion in § 3, the dispersion relation for a contaminated surface with non-trivial Marangoni effect and surface viscosity can be obtained from the determinant of the matrix
![]() $\unicode[STIX]{x1D648}$
, given by
$\unicode[STIX]{x1D648}$
, given by
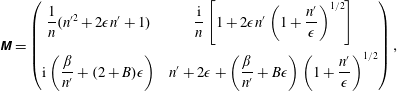
where we have considered the waveform solution

for the fluid velocities
![]() $u,v$
and the free surface
$u,v$
and the free surface
![]() $F$
, where
$F$
, where
![]() $A,C\in \mathbb{C}$
,
$A,C\in \mathbb{C}$
,
![]() $n=\text{i}\unicode[STIX]{x1D714}$
and
$n=\text{i}\unicode[STIX]{x1D714}$
and
![]() $n^{\prime }=\text{i}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}$
for
$n^{\prime }=\text{i}\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{0}$
for
and
Similarly, the pressure
![]() $p$
is given by
$p$
is given by
Evaluation of the determinant of
![]() $\unicode[STIX]{x1D648}$
gives
$\unicode[STIX]{x1D648}$
gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(Z^{4}-1+\frac{1}{\unicode[STIX]{x1D716}^{2}}\right)\left[1+Z^{2}+\left(\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}+B\right)Z\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{1}{\unicode[STIX]{x1D716}^{2}}+2(Z^{2}-1)Z\right)\left[2+B+\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(Z^{4}-1+\frac{1}{\unicode[STIX]{x1D716}^{2}}\right)\left[1+Z^{2}+\left(\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}+B\right)Z\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\frac{1}{\unicode[STIX]{x1D716}^{2}}+2(Z^{2}-1)Z\right)\left[2+B+\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}\right],\end{eqnarray}$$
where
Factorisation yields
 $$\begin{eqnarray}\displaystyle W_{0}(Z;\unicode[STIX]{x1D716})\left(1+Z+B+\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}\right) & & \displaystyle \nonumber\\ \displaystyle =-\left(\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}+B\right) & (Z-1)^{3}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{0}(Z;\unicode[STIX]{x1D716})\left(1+Z+B+\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}\right) & & \displaystyle \nonumber\\ \displaystyle =-\left(\frac{\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D716}^{2}(Z^{2}-1)}+B\right) & (Z-1)^{3}, & \displaystyle\end{eqnarray}$$
where
![]() $W_{0}(Z;\unicode[STIX]{x1D716})=0$
is the dispersion relation clean case result. This can be shown if we let
$W_{0}(Z;\unicode[STIX]{x1D716})=0$
is the dispersion relation clean case result. This can be shown if we let
![]() $\unicode[STIX]{x1D6FD},B=0$
in (B 8), i.e.
$\unicode[STIX]{x1D6FD},B=0$
in (B 8), i.e.
Factorisation gives
which reduces to
if we neglect the spurious root
![]() $Z+1=0$
.
$Z+1=0$
.






