Article contents
Changes in the boundary-layer structure at the edge of the ultimate regime in vertical natural convection
Published online by Cambridge University Press: 21 July 2017
Abstract
In thermal convection for very large Rayleigh numbers ( 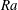 $Ra$ ), the thermal and viscous boundary layers are expected to undergo a transition from a classical state to an ultimate state. In the former state, the boundary-layer thicknesses follow a laminar-like Prandtl–Blasius–Polhausen scaling, whereas in the latter, the boundary layers are turbulent with logarithmic corrections in the sense of Prandtl and von Kármán. Here, we report evidence of this transition via changes in the boundary-layer structure of vertical natural convection (VC), which is a buoyancy-driven flow between differentially heated vertical walls. The numerical dataset spans
$Ra$ ), the thermal and viscous boundary layers are expected to undergo a transition from a classical state to an ultimate state. In the former state, the boundary-layer thicknesses follow a laminar-like Prandtl–Blasius–Polhausen scaling, whereas in the latter, the boundary layers are turbulent with logarithmic corrections in the sense of Prandtl and von Kármán. Here, we report evidence of this transition via changes in the boundary-layer structure of vertical natural convection (VC), which is a buoyancy-driven flow between differentially heated vertical walls. The numerical dataset spans 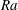 $Ra$ values from
$Ra$ values from 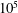 $10^{5}$ to
$10^{5}$ to 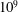 $10^{9}$ and a constant Prandtl number value of
$10^{9}$ and a constant Prandtl number value of 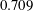 $0.709$ . For this
$0.709$ . For this 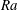 $Ra$ range, the VC flow has been previously found to exhibit classical state behaviour in a global sense. Yet, with increasing
$Ra$ range, the VC flow has been previously found to exhibit classical state behaviour in a global sense. Yet, with increasing 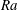 $Ra$ , we observe that near-wall higher-shear patches occupy increasingly larger fractions of the wall areas, which suggest that the boundary layers are undergoing a transition from the classical state to the ultimate shear-dominated state. The presence of streaky structures – reminiscent of the near-wall streaks in canonical wall-bounded turbulence – further supports the notion of this transition. Within the higher-shear patches, conditionally averaged statistics yield a logarithmic variation in the local mean temperature profiles, in agreement with the log law of the wall for mean temperature, and an
$Ra$ , we observe that near-wall higher-shear patches occupy increasingly larger fractions of the wall areas, which suggest that the boundary layers are undergoing a transition from the classical state to the ultimate shear-dominated state. The presence of streaky structures – reminiscent of the near-wall streaks in canonical wall-bounded turbulence – further supports the notion of this transition. Within the higher-shear patches, conditionally averaged statistics yield a logarithmic variation in the local mean temperature profiles, in agreement with the log law of the wall for mean temperature, and an 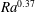 $Ra^{0.37}$ effective power-law scaling of the local Nusselt number. The scaling of the latter is consistent with the logarithmically corrected
$Ra^{0.37}$ effective power-law scaling of the local Nusselt number. The scaling of the latter is consistent with the logarithmically corrected 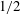 $1/2$ power-law scaling predicted for ultimate thermal convection for very large
$1/2$ power-law scaling predicted for ultimate thermal convection for very large 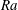 $Ra$ . Collectively, the results from this study indicate that turbulent and laminar-like boundary layer coexist in VC at moderate to high
$Ra$ . Collectively, the results from this study indicate that turbulent and laminar-like boundary layer coexist in VC at moderate to high 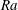 $Ra$ and this transition from the classical state to the ultimate state manifests as increasingly larger shear-dominated patches, consistent with the findings reported for Rayleigh–Bénard convection and Taylor–Couette flows.
$Ra$ and this transition from the classical state to the ultimate state manifests as increasingly larger shear-dominated patches, consistent with the findings reported for Rayleigh–Bénard convection and Taylor–Couette flows.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 44
- Cited by


