Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sun, Haomin
Sibamoto, Yasuteru
Okagaki, Yuria
and
Yonomoto, Taisuke
2019.
Experimental Investigation of Decontamination Factor Dependence on Aerosol Concentration in Pool Scrubbing.
Science and Technology of Nuclear Installations,
Vol. 2019,
Issue. ,
p.
1.
Hessenkemper, H.
Ziegenhein, T.
and
Lucas, D.
2020.
Contamination effects on the lift force of ellipsoidal air bubbles rising in saline water solutions.
Chemical Engineering Journal,
Vol. 386,
Issue. ,
p.
121589.
Faugaret, Antoine
Duguet, Yohann
Fraigneau, Yann
and
Martin Witkowski, Laurent
2020.
Influence of interface pollution on the linear stability of a rotating flow.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Rastello, Marie
and
Marié, Jean-Louis
2020.
Wake behind contaminated bubbles in a solid-body rotating flow.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Lee, Wooram
and
Lee, Jae-Young
2020.
Experiment and modeling of lift force acting on single high Reynolds number bubbles rising in linear shear flow.
Experimental Thermal and Fluid Science,
Vol. 115,
Issue. ,
p.
110085.
Hadikhani, Pooria
H. Hashemi, S. Mohammad
and
Psaltis, Demetri
2020.
The Impact of Surfactants on the Inertial Separation of Bubbles in Microfluidic Electrolyzers.
Journal of The Electrochemical Society,
Vol. 167,
Issue. 13,
p.
134504.
Freitas, Lucas Gusmão
Pereira, Luiz Antonio Alcântara
and
Lima e Silva, Ana Lúcia Fernandes de
2021.
Comparison among drag coefficient models of single bubbles under high and low Morton number regimes.
Chemical Engineering Science,
Vol. 236,
Issue. ,
p.
116473.
Rodgar, Majid
Scolan, Hélène
Marié, Jean-Louis
Doppler, Delphine
and
Matas, Jean-Philippe
2021.
Bubble behaviour in a horizontal high-speed solid-body rotating flow.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Haas, Tim
Schubert, Christian
Eickhoff, Moritz
and
Pfeifer, Herbert
2021.
A Review of Bubble Dynamics in Liquid Metals.
Metals,
Vol. 11,
Issue. 4,
p.
664.
Hessenkemper, H.
Ziegenhein, T.
Lucas, D.
and
Tomiyama, A.
2021.
Influence of surfactant contaminations on the lift force of ellipsoidal bubbles in water.
International Journal of Multiphase Flow,
Vol. 145,
Issue. ,
p.
103833.
Shi, Pengyu
Tholan, Vaishakh
Sommer, Anna-Elisabeth
Heitkam, Sascha
Eckert, Kerstin
Galvin, Kevin
and
Rzehak, Roland
2023.
Forces on a nearly spherical bubble rising in an inclined channel flow.
International Journal of Multiphase Flow,
Vol. 169,
Issue. ,
p.
104620.
Mandalahalli, Manas M.
Lif, Johan
Mudde, Robert F.
and
Portela, Luis M.
2023.
Electrolyte and temperature effects in a rising bubble.
Chemical Engineering Science,
Vol. 270,
Issue. ,
p.
118276.
Rodgar, Majid
Scolan, Hélène
Marié, Jean-Louis
Doppler, Delphine
and
Matas, Jean-Philippe
2023.
Bubble breakup and effects of soluble surfactants on bubble dynamics in a solid-body rotating flow.
Physical Review Fluids,
Vol. 8,
Issue. 7,
Estepa-Cantero, C.
Martínez-Bazán, C.
and
Bolaños-Jiménez, R.
2024.
Bubble rising near a vertical wall: Experimental characterization of paths and velocity.
Physics of Fluids,
Vol. 36,
Issue. 1,
Biswas, Subhajit
and
Govardhan, Raghuraman N.
2025.
Interaction of a vortex ring with a buoyant spherical particle: effects of particle size on vorticity dynamics and particle dynamics.
Journal of Fluid Mechanics,
Vol. 1015,
Issue. ,
Liu, Wen
Huang, Pingnan
and
Wu, Nan
2025.
Bubble Separation in a Gas–Liquid Swirling Pipe Flow.
Heat Transfer Engineering,
Vol. 46,
Issue. 16-17,
p.
1491.
Ma, Xiaojing
Wang, Songhe
Nong, ShiXin
Han, Chunjiao
Xu, Jinliang
and
Sefiane, Khellil
2025.
Study of bubble dynamics detaching from flexible channels.
International Journal of Heat and Mass Transfer,
Vol. 253,
Issue. ,
p.
127625.
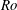 $Ro$ , contrary to the case of clean bubbles. Including the ‘spin’ induced lift component in the dynamical equations provides a better prediction of the bubble’s trajectory in contaminated fluid. The presence of contaminants immobilizes the rear part of the bubble and reduces significantly the deformation. The laws of deformation according to the nature of the surface are presented. The way deformation influences the drag and lift coefficients in pure and contaminated fluids is quantified and discussed. Expressions for these various coefficients are proposed.
$Ro$ , contrary to the case of clean bubbles. Including the ‘spin’ induced lift component in the dynamical equations provides a better prediction of the bubble’s trajectory in contaminated fluid. The presence of contaminants immobilizes the rear part of the bubble and reduces significantly the deformation. The laws of deformation according to the nature of the surface are presented. The way deformation influences the drag and lift coefficients in pure and contaminated fluids is quantified and discussed. Expressions for these various coefficients are proposed.

