Article contents
Clustering and increased settling speed of oblate particles at finite Reynolds number
Published online by Cambridge University Press: 11 June 2018
Abstract
We study the settling of rigid oblates in a quiescent fluid using interface-resolved direct numerical simulations. In particular, an immersed boundary method is used to account for the dispersed solid phase together with lubrication correction and collision models to account for short-range particle–particle interactions. We consider semi-dilute suspensions of oblate particles with aspect ratio 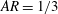 $AR=1/3$ and solid volume fractions
$AR=1/3$ and solid volume fractions 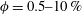 $\unicode[STIX]{x1D719}=0.5{-}10\,\%$ . The solid-to-fluid density ratio
$\unicode[STIX]{x1D719}=0.5{-}10\,\%$ . The solid-to-fluid density ratio 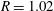 $R=1.02$ and the Galileo number (i.e. the ratio between buoyancy and viscous forces) based on the diameter of a sphere with equivalent volume
$R=1.02$ and the Galileo number (i.e. the ratio between buoyancy and viscous forces) based on the diameter of a sphere with equivalent volume 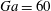 $Ga=60$ . With this choice of parameters, an isolated oblate falls vertically with a steady wake with its broad side perpendicular to the gravity direction. At this
$Ga=60$ . With this choice of parameters, an isolated oblate falls vertically with a steady wake with its broad side perpendicular to the gravity direction. At this 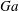 $Ga$ , the mean settling speed of spheres is a decreasing function of the volume
$Ga$ , the mean settling speed of spheres is a decreasing function of the volume 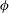 $\unicode[STIX]{x1D719}$ and is always smaller than the terminal velocity of the isolated particle,
$\unicode[STIX]{x1D719}$ and is always smaller than the terminal velocity of the isolated particle, 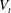 $V_{t}$ . On the contrary, in dilute suspensions of oblate particles (with
$V_{t}$ . On the contrary, in dilute suspensions of oblate particles (with 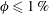 $\unicode[STIX]{x1D719}\leqslant 1\,\%$ ), the mean settling speed is approximately 33 % larger than
$\unicode[STIX]{x1D719}\leqslant 1\,\%$ ), the mean settling speed is approximately 33 % larger than 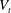 $V_{t}$ . At higher concentrations, the mean settling speed decreases becoming smaller than the terminal velocity
$V_{t}$ . At higher concentrations, the mean settling speed decreases becoming smaller than the terminal velocity 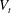 $V_{t}$ between
$V_{t}$ between 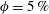 $\unicode[STIX]{x1D719}=5\,\%$ and 10 %. The increase of the mean settling speed is due to the formation of particle clusters that for
$\unicode[STIX]{x1D719}=5\,\%$ and 10 %. The increase of the mean settling speed is due to the formation of particle clusters that for 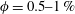 $\unicode[STIX]{x1D719}=0.5{-}1\,\%$ appear as columnar-like structures. From the pair distribution function we observe that it is most probable to find particle pairs almost vertically aligned. However, the pair distribution function is non-negligible all around the reference particle indicating that there is a substantial amount of clustering at radial distances between 2 and
$\unicode[STIX]{x1D719}=0.5{-}1\,\%$ appear as columnar-like structures. From the pair distribution function we observe that it is most probable to find particle pairs almost vertically aligned. However, the pair distribution function is non-negligible all around the reference particle indicating that there is a substantial amount of clustering at radial distances between 2 and 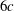 $6c$ (with
$6c$ (with  $c$ the polar radius of the oblate). Above
$c$ the polar radius of the oblate). Above 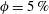 $\unicode[STIX]{x1D719}=5\,\%$ , the hindrance becomes the dominant effect, and the mean settling speed decreases below
$\unicode[STIX]{x1D719}=5\,\%$ , the hindrance becomes the dominant effect, and the mean settling speed decreases below 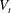 $V_{t}$ . As the particle concentration increases, the mean particle orientation changes and the mean pitch angle (the angle between the particle axis of symmetry and gravity) increases from
$V_{t}$ . As the particle concentration increases, the mean particle orientation changes and the mean pitch angle (the angle between the particle axis of symmetry and gravity) increases from 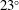 $23^{\circ }$ to
$23^{\circ }$ to 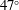 $47^{\circ }$ . Finally, we increase
$47^{\circ }$ . Finally, we increase 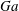 $Ga$ from 60 to 140 for the case with
$Ga$ from 60 to 140 for the case with 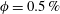 $\unicode[STIX]{x1D719}=0.5\,\%$ and find that the mean settling speed (normalized by
$\unicode[STIX]{x1D719}=0.5\,\%$ and find that the mean settling speed (normalized by 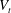 $V_{t}$ ) decreases by less than 1 % with respect to
$V_{t}$ ) decreases by less than 1 % with respect to 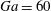 $Ga=60$ . However, the fluctuations of the settling speed around the mean are reduced and the probability of finding vertically aligned particle pairs increases.
$Ga=60$ . However, the fluctuations of the settling speed around the mean are reduced and the probability of finding vertically aligned particle pairs increases.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 28
- Cited by


