Article contents
Coffee stain effect on a fibre from axisymmetric droplets
Published online by Cambridge University Press: 27 February 2023
Abstract
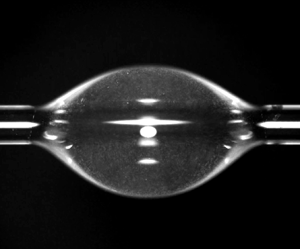
The so-called coffee stain effect has been intensively studied over the past decades, but most of the studies have focused on sessile droplets. In this paper, we analyse the origin of the difference between the deposition of suspended particles in a sessile drop and in an axisymmetric drop deposited on a fibre. First, we model the shape of a drop on a fibre and its evaporative flux with some approximations to derive analytical calculations. Then, for pinned contact lines, we solve the hydrodynamics equations in the liquid phase under the lubrication approximation to determine the flow velocity toward the contact lines. We comment on these results by comparison to a sessile drop of similar evaporating conditions, and we show that the substrate curvature plays a role on the contact line depinning, the local evaporative flux and the liquid flow field. The competition between the advection and the Brownian motion indicates that the transport of the particles toward the contact line occurs in a volume localised in the close vicinity of the contact lines for a drop on a fibre. Thus, the fibre geometry induces a weaker accumulation of particles at the contact line compared to a sessile drop, leading to the more homogeneous deposit observed experimentally.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by


