Hostname: page-component-5b777bbd6c-2hk6m Total loading time: 0 Render date: 2025-06-20T20:51:22.422Z Has data issue: false hasContentIssue false
  • English
  • Français

Combined Reynolds-vorticity transport analysis of the shear layers in a premixed swirling flame

Published online by Cambridge University Press:  14 March 2025

Qiuxiao Wang ,
Shuyue Lai ,
Fei Qi Open the ORCID record for Fei Qi [Opens in a new window]  and
Xi Xia Open the ORCID record for Xi Xia [Opens in a new window]
Qiuxiao Wang
Affiliation:
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Shuyue Lai
Affiliation:
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Fei Qi
Affiliation:
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
Xi Xia*
Affiliation:
School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, PR China
*
Corresponding author: Xi Xia, xiaxiss@sjtu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

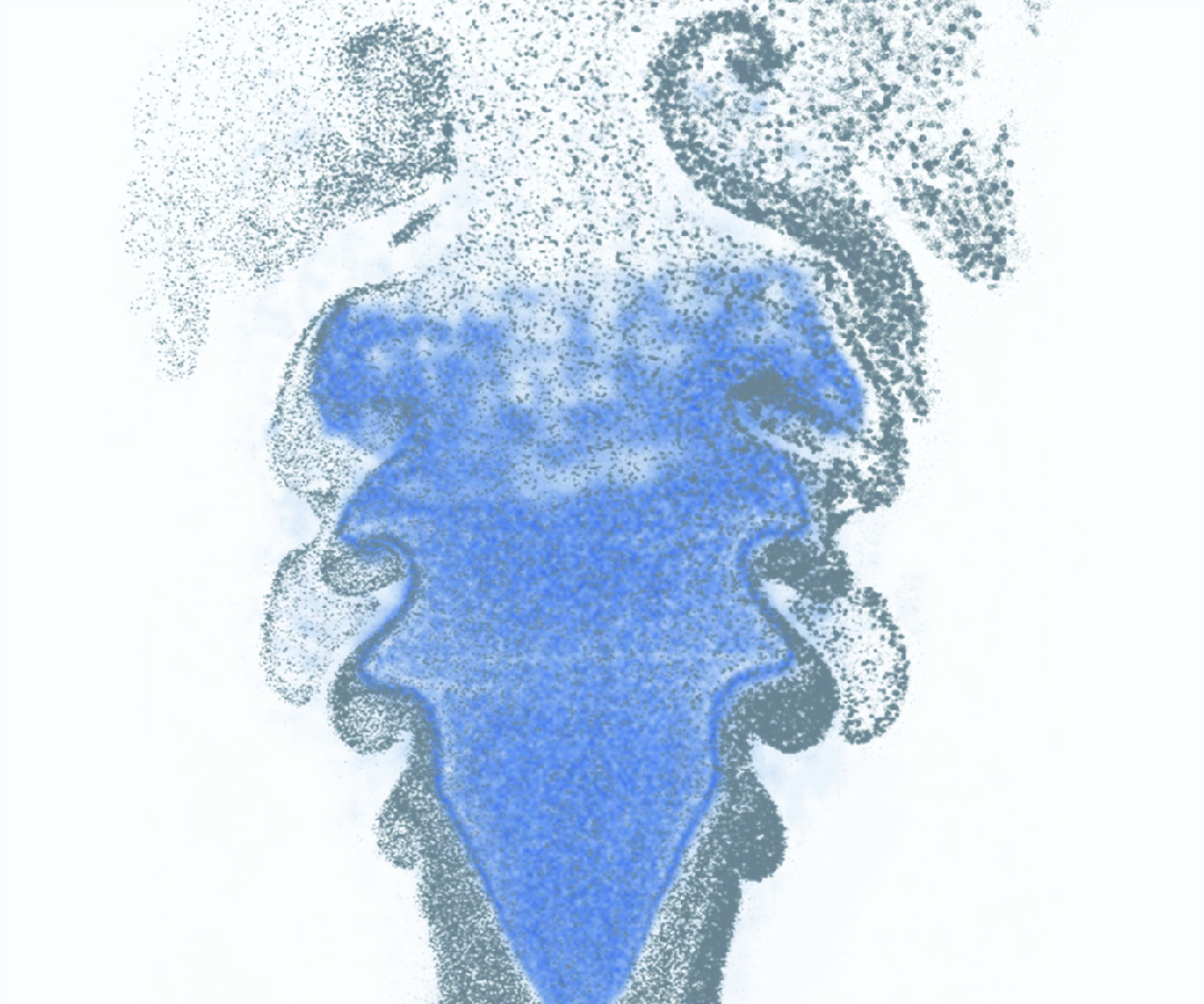
This work focuses on the intensity variation mechanisms in the mean inner and outer shear layers of a premixed swirling flame. In order to close the gap between the Lagrangian vorticity transport and the Eulerian shear layer intensity ($\gamma$), we propose a combined Reynolds-vorticity transport approach to obtain the streamwise variation of $\gamma$ as the integrals of vorticity generation terms, including tilting, baroclinic torque, diffusion and dilatation. However, different from the classical vorticity (transport) equation, the vortex stretching vanishes, and the original dilatation is replaced by a shear-layer dilatation in the new model. It enables the quantitative evaluation of how the different vorticity transport terms affect the shear layer intensity; in particular, we have identified vortex tilting and baroclinic torque as the main cause of the inner shear layer enhancement in the swirling flame’s near field. Although this model is initially developed to study the flame-attached shear layers, the broader significance lies in its applicability to general axisymmetric shear flows.

JFM classification

Reacting Flows: Flames Wakes/Jets: Shear layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1006 , 10 March 2025 , A20
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Balachandran, R., Ayoola, B.O., Kaminski, C.F., Dowling, A.P. & Mastorakos, E. 2005 Experimental investigation of the nonlinear response of turbulent premixed flames to imposed inlet velocity oscillations. Combust. Flame 143 (1–2), 37–55.CrossRefGoogle Scholar
Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.CrossRefGoogle Scholar
Batchelor, G.K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Brøns, M., Thompson, M.C., Leweke, T. & Hourigan, K. 2014 Vorticity generation and conservation for two-dimensional interfaces and boundaries. J. Fluid Mech. 758, 63–93.CrossRefGoogle Scholar
Candel, S., Durox, D., Schuller, T., Bourgouin, J.F. & Moeck, J.P. 2014 Dynamics of swirling flames. Annu. Rev. Fluid Mech. 46 (1), 147–173.CrossRefGoogle Scholar
Caulfield, C.P. 2021 Layering, instabilities, and mixing in turbulent stratified flows. Annu. Rev. Fluid Mech. 53 (1), 113–145.CrossRefGoogle Scholar
Danaila, I., Kaplanski, F. & Sazhin, S.S. 2021 Vortex Ring Models. Springer.CrossRefGoogle Scholar
Dasch, C.J. 1992 One-dimensional tomography: a comparison of Abel, onion-peeling, and filtered backprojection methods. Appl. Opt. 31 (8), 1146–1152.CrossRefGoogle ScholarPubMed
Deardorff, J.W. & Willis, G.E. 1982 Dependence of mixed-layer entrainment on shear stress and velocity jump. J. Fluid Mech. 115,123–149.CrossRefGoogle Scholar
Douglas, C.M., Emerson, B.L., Hemchandra, S. & Lieuwen, T.C. 2021 Forced flow response analysis of a turbulent swirling annular jet flame. Phys. Fluids 33 (8), 085124.CrossRefGoogle Scholar
Durst, F. & Arnold, I. 2008 Fluid Mechanics: An Introduction to the Theory of Fluid Flows. Springer.CrossRefGoogle Scholar
Gao, L. & Yu, S. 2012 Development of the trailing shear layer in a starting jet during pinch-off. J. Fluid Mech. 700, 382–405.CrossRefGoogle Scholar
Geikie, M.K. & Ahmed, K.A. 2018 Pressure-gradient tailoring effects on the turbulent flame–vortex dynamics of bluff-body premixed flames. Combust. Flame 197, 227–242.CrossRefGoogle Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Jahanbakhshi, R., Vaghefi, N.S. & Madnia, C.K. 2015 Baroclinic vorticity generation near the turbulent/non-turbulent interface in a compressible shear layer. Phys. Fluids 27 (10), 105105.CrossRefGoogle Scholar
Kaminski, A.K., Caulfield, C.P. & Taylor, J.R. 2014 Transient growth in strongly stratified shear layers. J. Fluid Mech. 758, R4.CrossRefGoogle Scholar
Kazbekov, A., Kumashiro, K. & Steinberg, A.M. 2019 Enstrophy transport in swirl combustion. J. Fluid Mech. 876, 715–732.CrossRefGoogle Scholar
Kazbekov, A. & Steinberg, A.M. 2021 Flame- and flow-conditioned vorticity transport in premixed swirl combustion. Proc. Combust. Inst. 38 (2), 2949–2956.CrossRefGoogle Scholar
Konle, M. & Sattelmayer, T. 2009 Interaction of heat release and vortex breakdown during flame flashback driven by combustion induced vortex breakdown. Exp. Fluids 47 (4–5), 627–635.CrossRefGoogle Scholar
Lin, C.C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lundgren, T. & Koumoutsakos, P. 1999 On the generation of vorticity at a free surface. J. Fluid Mech. 382, 351–366.CrossRefGoogle Scholar
Morris, S.C. 2011 Shear-layer instabilities: particle image velocimetry measurements and implications for acoustics. Annu. Rev. Fluid Mech. 43 (1), 529–550.CrossRefGoogle Scholar
Oberleithner, K., Schimek, S. & Paschereit, C.O. 2015 Shear flow instabilities in swirl-stabilized combustors and their impact on the amplitude dependent flame response: a linear stability analysis. Combust. Flame 162 (1), 86–99.CrossRefGoogle Scholar
Pawlak, G. & Armi, L. 1998 Vortex dynamics in a spatially accelerating shear layer. J. Fluid Mech. 376, 1–35.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ren, Y., Wang, Q., Peng, Y., Xu, L., Xia, X. & Qi, F. 2024 Strong and weak interactions of a V-shaped premixed swirling flame with outer vortex rings. Combust. Flame 270, 113760.CrossRefGoogle Scholar
Renard, P.H., Thevenin, D., Rolon, J.C. & Candel, S. 2000 Dynamics of flame/vortex interactions. Prog. Energy Combust. Sci. 26 (3), 225–282.CrossRefGoogle Scholar
Rising, C.J., Morales, A.J., Geikie, M.K. & Ahmed, K.A. 2021 The effects of turbulence and pressure gradients on vorticity transport in premixed bluff-body flames. Phys. Fluids 33 (1), 017106.CrossRefGoogle Scholar
Rosi, G.A. & Rival, D.E. 2017 Entrainment and topology of accelerating shear layers. J. Fluid Mech. 811, 37–50.CrossRefGoogle Scholar
Rukes, L., Sieber, M., Oberleithner, K., Nayeri, C. & Paschereit, C.O. 2015 The influence of the inner shear layer on the suppression of the global mode in heated swirling jets. In 53rd AIAA Aerospace Sciences Meeting. AIAA 2015-0302.CrossRefGoogle Scholar
Smith, K.M., Caulfield, C.P. & Taylor, J.R. 2021 Turbulence in forced stratified shear flows. J. Fluid Mech. 910, A42.CrossRefGoogle Scholar
Soteriou, M.C. & Ghoniem, A.F. 1994 The vorticity dynamics of an exothermic, spatially developing, forced, reacting shear layer. Symp. (Int.) Combust. 25 (1), 1265–1272.CrossRefGoogle Scholar
Stöhr, M., Boxx, I., Carter, C. & Meier, W. 2012 Experimental study of vortex–flame interaction in a gas turbine model combustor. Combust. Flame 159 (8), 2636–2649.CrossRefGoogle Scholar
Syred, N. & Beér, J.M. 1974 Combustion in swirling flows: a review. Combust. Flame 23 (2), 143–201.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M.P. 2016 Coherent structures in a swirl injector at $Re=4800$ by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Thumuluru, S.K. & Lieuwen, T. 2009 Characterization of acoustically forced swirl flame dynamics. Proc. Combust. Inst. 32 (2), 2893–2900.CrossRefGoogle Scholar
Tsai, W.T. 1998 A numerical study of the evolution and structure of a turbulent shear layer under a free surface. J. Fluid Mech. 354, 239–276.CrossRefGoogle Scholar
Vanderkindere, J.W., Laskari, A., Ganapathisubramani, B. & Dekat, R. 2019 Pressure from 2D snapshot PIV. Exp. Fluids 60, 1–18.Google Scholar
Wang, G., Liu, X., Xia, X., Wang, S. & Qi, F. 2021 Dynamics of periodically-excited vortices in swirling flames. Proc. Combust. Inst. 38 (4), 6183–6191.CrossRefGoogle Scholar
Wang, Q., Ren, Y., Gu, M., Yu, B., Feng, X., Qi, F. & Xia, X. 2023 Influence of inner shear layer on the emergence of central recirculation zone in a V-shaped premixed swirling flame. Phys. Fluids 35 (10), 107129.CrossRefGoogle Scholar
Wang, S. et al. 2022 Evolution characteristics of 3D vortex structures in stratified swirling flames studied by dual-plane stereoscopic PIV. Combust. Flame 237, 111874.CrossRefGoogle Scholar
White, F.M. & Majdalani, J. 2006 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Wieneke, B. 2005 Stereo-PIV using self-calibration on particle images. Exp. Fluids 39 (2), 267–280.CrossRefGoogle Scholar
Xia, X. & Zhang, P. 2018 A vortex-dynamical scaling theory for flickering buoyant diffusion flames. J. Fluid Mech. 855, 1156–1169.CrossRefGoogle Scholar