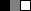1 Introduction
Intermittency is a ubiquitous feature that can be observed over a wide range of dynamic systems arising in engineering and nature. Turbulent shear flows, ocean waves, weather patterns, seismic events and volcanic eruptions are but a few examples that are characterized by the irregular occurrence of events far from the statistical mean. Classically, intermittency is quantified in terms of a binary intermittency function or an intermittency factor that describes the probability of finding the flow in one state or the other. Once identified, this factor can be used as a filter to obtain conditional statistics for each state independently (Pope Reference Pope2000). While these statistics might accurately describe the random process in a quantitative manner via its moments, the underlying physics is often better understood from a dynamical systems perspective. In this light, sporadic deviations from the statistical equilibrium can, for many systems, be expressed as instabilities that are intermittently triggered through external stochastic excitation (Mohamad & Sapsis Reference Mohamad and Sapsis2015). If the amplification potential and growth rate of these instabilities are significant, a statistical footprint in the process’s distributional tails can be observed and related to intermittent, rare events.
In the context of fluid mechanics, transient growth, associated with the non-normality of the underlying linearized dynamics (Trefethen et al. Reference Trefethen, Trefethen, Reddy and Driscoll1993; Farrell & Ioannou Reference Farrell and Ioannou1996; Schmid & Henningson Reference Schmid and Henningson2001), provides such an amplification mechanism. The linear theory that governs transient growth allows for the computation of non-modal solutions that identify spatial structures that undergo significant energy growth over short periods of time. Pipe flow is a prominent example of a flow in which a transient linear amplification process plays a crucial role as the flow transitions from the laminar to an intermittently turbulent state with increasing flow rate (Kerswell Reference Kerswell2005; Avila et al. Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011). In particular, patches of turbulence, so-called turbulent puffs, are observed despite the fact that the laminar state is linearly stable to infinitesimal disturbances. In other systems, nonlinear interactions may sporadically conspire in such a way that responses of exceptionally large amplitudes are observed. Such statistical outliers are commonly referred to as extreme, or rare events due to their isolated nature. An example of this class of intermittent effects is given by oceanographic surface gravity waves of extreme magnitude, or rogue waves (Dysthe, Krogstad & Müller Reference Dysthe, Krogstad and Müller2008).
Figure 1. A high-energy burst in the acoustic far field of a turbulent jet: (a) scaleogram of the
![]() $m=1$
component of the pressure signal at the probe location (magenta dot) at
$m=1$
component of the pressure signal at the probe location (magenta dot) at
![]() $(x_{0},r_{0})=(12,5)$
; (b,c) streamwise fluctuation velocity in the centre plane (coloured contours) and
$(x_{0},r_{0})=(12,5)$
; (b,c) streamwise fluctuation velocity in the centre plane (coloured contours) and
![]() $m=1$
pressure component (greyscale contours) at
$m=1$
pressure component (greyscale contours) at
![]() $t=366.8$
in (b) and
$t=366.8$
in (b) and
![]() $t=378$
in (c). The two time instances represent the peak of the loud event identified in the scaleogram by the 75 % of maximum pressure contour (red) and the quiet period shortly thereafter. The green lines in (b,c) indicate where the streamwise mean velocity corresponds to 10 % of the jet velocity, i.e.
$t=378$
in (c). The two time instances represent the peak of the loud event identified in the scaleogram by the 75 % of maximum pressure contour (red) and the quiet period shortly thereafter. The green lines in (b,c) indicate where the streamwise mean velocity corresponds to 10 % of the jet velocity, i.e.
![]() $U(\boldsymbol{x})=0.1U_{j}$
, for later use in (3.3). A standard Morse wavelet is used in (a). All contour levels are adjusted for best readability.
$U(\boldsymbol{x})=0.1U_{j}$
, for later use in (3.3). A standard Morse wavelet is used in (a). All contour levels are adjusted for best readability.
In this paper, we present a data-driven approach to isolate and identify intermittent structures in a statistical manner by leveraging both their temporal and spatial coherence. The method builds on a general space–time POD formalism, as introduced in the original work of Lumley (Reference Lumley1970) and discussed in detail in § 2, to find structures that optimally represent the data in terms of variance, or energy, and combines it with the idea of conditional averaging to isolate a specific event from unconditional data. The use of conditional averages to study flow patterns dates back to the pioneering work of Adrian (Reference Adrian1975), who introduced the method of linear stochastic estimation (LSE) to educe conditional flow structures from isotropic turbulence. LSE establishes a linear mapping between a conditional event and a conditionally averaged flow variable. The mapping is computed from a minimization argument between the cross-correlation of the event data and the conditional flow state to be estimated. It is then used to compute conditionally averaged estimates from unconditionally sampled two-point correlations. Stochastic estimation has been extended from single- to multi-time estimates in the frequency domain (Ewing & Citriniti Reference Ewing and Citriniti1999; Tinney et al. Reference Tinney, Coiffet, Delville, Hall, Jordan and Glauser2006) and used in conjunction with POD (Bonnet et al. Reference Bonnet, Cole, Delville, Glauser and Ukeiley1994). Unlike LSE, the present method does not rely on the a priori definition of a candidate structure, the so-called ‘conditional eddy’, but identifies the energetically dominant structure by means of an eigenvalue decomposition of the conditional two-point space–time correlation tensor.
As an example, we choose the highly intermittent acoustic Mach wave acoustic radiation of a hot turbulent jet. The jet-noise problem is of eminent technical interest for the aviation industry, in particular as it applies to naval aviation: aircraft carrier flight crew personnel operate in one of the world’s loudest work environments, and regularly suffer from hearing loss due to overexposure to intermittent noise (Aubert & McKinley Reference Aubert and McKinley2011). In figure 1, we contrast two time instances of the flow field obtained from a high-fidelity numerical simulation (Brès et al. Reference Brès, Ham, Nichols and Lele2017). As in Kœnig et al. (Reference Kœnig, Cavalieri, Jordan, Delville, Gervais and Papamoschou2013), we use a wavelet transform of the pressure signal at a probe location in the far field to identify loud events, or acoustic bursts, and distinguish them from quieter periods in which the pressure fluctuations are closer to their statistical mean.
A loud event is identified from the scaleogram in figure 1(a) and the corresponding perturbation velocity and pressure fields for the
![]() $m=1$
azimuthal Fourier component are shown in figure 1(b). The acoustic burst manifests itself as a high-amplitude wave in the pressure field that is emitted at a low angle (relative to the jet axis) from the jet. Shortly after, the pressure field at the probe location appears quiet in figure 1(c). It is well established that large-scale coherent structures, or wavepackets, are the dominant source of low aft-angle jet noise and that these structures can be modelled as spatial linear stability modes (Jordan & Colonius Reference Jordan and Colonius2013) or resolvent modes (Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018). Their footprint can be seen in the pressure field in the developing jet region with
$m=1$
azimuthal Fourier component are shown in figure 1(b). The acoustic burst manifests itself as a high-amplitude wave in the pressure field that is emitted at a low angle (relative to the jet axis) from the jet. Shortly after, the pressure field at the probe location appears quiet in figure 1(c). It is well established that large-scale coherent structures, or wavepackets, are the dominant source of low aft-angle jet noise and that these structures can be modelled as spatial linear stability modes (Jordan & Colonius Reference Jordan and Colonius2013) or resolvent modes (Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018). Their footprint can be seen in the pressure field in the developing jet region with
![]() $x\lesssim 10$
in figure 1(b,c). A salient feature of wavepackets that is not represented by these modal solutions is their intermittent behaviour, or jitter. Intimately linked to the jitter of the shear-layer instabilities, however, is the intermittency of the sound they radiate. The stochastic nature of jet noise has been measured (Juvé, Sunyach & Comte-Bellot Reference Juvé, Sunyach and Comte-Bellot1980; Kearney-Fischer, Sinha & Samimy Reference Kearney-Fischer, Sinha and Samimy2013), quantified and modelled (Cavalieri et al.
Reference Cavalieri, Jordan, Agarwal and Gervais2011), but is not fully understood as of now.
$x\lesssim 10$
in figure 1(b,c). A salient feature of wavepackets that is not represented by these modal solutions is their intermittent behaviour, or jitter. Intimately linked to the jitter of the shear-layer instabilities, however, is the intermittency of the sound they radiate. The stochastic nature of jet noise has been measured (Juvé, Sunyach & Comte-Bellot Reference Juvé, Sunyach and Comte-Bellot1980; Kearney-Fischer, Sinha & Samimy Reference Kearney-Fischer, Sinha and Samimy2013), quantified and modelled (Cavalieri et al.
Reference Cavalieri, Jordan, Agarwal and Gervais2011), but is not fully understood as of now.
In § 2, we first formulate the conditional space–time POD problem that allows for the inference of intermittent or rare events as space–time modes that optimally capture the conditional variance of an ensemble of realizations of the event. As an example, we then apply the general framework to acoustic bursts in turbulent jets in § 3, before summarizing our findings in § 4.
2 A conditional space–time POD formulation
We start by defining the space–time inner product
on which we also base a measure of perturbation size as the energy (norm) of the quantity
![]() $\boldsymbol{q}.$
The diagonal, positive definite weight matrix
$\boldsymbol{q}.$
The diagonal, positive definite weight matrix
![]() $\unicode[STIX]{x1D652}(\boldsymbol{x})$
is introduced to accommodate space- and/or variable-dependent weights.
$\unicode[STIX]{x1D652}(\boldsymbol{x})$
is introduced to accommodate space- and/or variable-dependent weights.
Equipped with the scalar product
![]() $\langle \cdot \,,\cdot \rangle _{\boldsymbol{x},t}$
and an expectation operator
$\langle \cdot \,,\cdot \rangle _{\boldsymbol{x},t}$
and an expectation operator
![]() $E\{\cdot \}$
, commonly defined as the sample average, we embed
$E\{\cdot \}$
, commonly defined as the sample average, we embed
![]() $\boldsymbol{q}(\boldsymbol{x},t)$
into a Hilbert space
$\boldsymbol{q}(\boldsymbol{x},t)$
into a Hilbert space
![]() ${\mathcal{H}}$
, which allows us to identify the spatio-temporal structure
${\mathcal{H}}$
, which allows us to identify the spatio-temporal structure
![]() $\unicode[STIX]{x1D753}(\boldsymbol{x},t)\in {\mathcal{H}}$
that maximizes
$\unicode[STIX]{x1D753}(\boldsymbol{x},t)\in {\mathcal{H}}$
that maximizes
using a variational approach. The
![]() $\unicode[STIX]{x1D753}(\boldsymbol{x},t)$
and
$\unicode[STIX]{x1D753}(\boldsymbol{x},t)$
and
![]() $\unicode[STIX]{x1D706}$
that satisfy (2.2) can be found as solutions to the Fredholm eigenvalue problem
$\unicode[STIX]{x1D706}$
that satisfy (2.2) can be found as solutions to the Fredholm eigenvalue problem
where
![]() $\unicode[STIX]{x1D63E}(\boldsymbol{x},\boldsymbol{x}^{\prime },t,t^{\prime })=E\{\boldsymbol{q}(\boldsymbol{x},t)\boldsymbol{q}^{\ast }(\boldsymbol{x}^{\prime },t^{\prime })\}$
denotes the two-point space–time correlation tensor. This formulation corresponds to the classical space–time POD problem introduced by Lumley (Reference Lumley1970), which was vastly overshadowed by its popular spatial variant (Sirovich Reference Sirovich1987; Aubry Reference Aubry1991). A notable exception is the work by Gordeyev & Thomas (Reference Gordeyev and Thomas2013), in which the authors solve a space–time POD problem to investigate flow transients. More recently, the frequency-domain version (see Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018; Towne, Schmidt & Colonius Reference Towne, Schmidt and Colonius2018), which is derived from (2.3) under the assumption of statistical stationarity, has gained popularity in the analysis of turbulent flows.
$\unicode[STIX]{x1D63E}(\boldsymbol{x},\boldsymbol{x}^{\prime },t,t^{\prime })=E\{\boldsymbol{q}(\boldsymbol{x},t)\boldsymbol{q}^{\ast }(\boldsymbol{x}^{\prime },t^{\prime })\}$
denotes the two-point space–time correlation tensor. This formulation corresponds to the classical space–time POD problem introduced by Lumley (Reference Lumley1970), which was vastly overshadowed by its popular spatial variant (Sirovich Reference Sirovich1987; Aubry Reference Aubry1991). A notable exception is the work by Gordeyev & Thomas (Reference Gordeyev and Thomas2013), in which the authors solve a space–time POD problem to investigate flow transients. More recently, the frequency-domain version (see Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018; Towne, Schmidt & Colonius Reference Towne, Schmidt and Colonius2018), which is derived from (2.3) under the assumption of statistical stationarity, has gained popularity in the analysis of turbulent flows.
In deviation from other formulations, we introduce a conditional expectation
with respect to the event
![]() $H$
. As we are interested in the average evolution of the extreme event in space and time, we furthermore recast the space–time inner product (2.5) into a weighted space–time inner product
$H$
. As we are interested in the average evolution of the extreme event in space and time, we furthermore recast the space–time inner product (2.5) into a weighted space–time inner product
over some finite time horizon
![]() $\unicode[STIX]{x0394}T$
in the temporal neighbourhood of the extreme event
$\unicode[STIX]{x0394}T$
in the temporal neighbourhood of the extreme event
![]() $H$
. The quantity to maximize
$H$
. The quantity to maximize
is defined analogously to (2.2) and its solution is obtained, analogous to (2.3), from the corresponding weighted Fredholm eigenvalue problem
In discrete time and space, the eigenvalues and eigenvectors of the two-point space–time correlation tensor are obtained from the decomposition
where
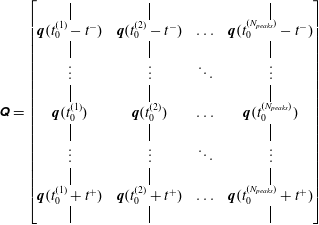
represents the space–time data matrix of realizations of events occurring at times
![]() $t_{0}^{(j)}$
. The
$t_{0}^{(j)}$
. The
![]() $j$
th column of
$j$
th column of
![]() $\unicode[STIX]{x1D64C}$
hence contains the
$\unicode[STIX]{x1D64C}$
hence contains the
![]() $j$
th realization of event
$j$
th realization of event
![]() $H$
evolving from time
$H$
evolving from time
![]() $t_{0}^{(j)}-t^{-}$
to
$t_{0}^{(j)}-t^{-}$
to
![]() $t_{0}^{(j)}+t^{+}$
, i.e. over
$t_{0}^{(j)}+t^{+}$
, i.e. over
![]() $\unicode[STIX]{x0394}T/\unicode[STIX]{x0394}t$
time steps. Here,
$\unicode[STIX]{x0394}T/\unicode[STIX]{x0394}t$
time steps. Here,
![]() $\unicode[STIX]{x0394}t$
is the temporal separation between two consecutive snapshots, and
$\unicode[STIX]{x0394}t$
is the temporal separation between two consecutive snapshots, and
![]() $t^{-}$
and
$t^{-}$
and
![]() $t^{+}$
define the time interval
$t^{+}$
define the time interval
over which the
![]() $j$
th event evolves, with
$j$
th event evolves, with
![]() $\unicode[STIX]{x0394}T^{(j)}$
denoting its length. The matrix
$\unicode[STIX]{x0394}T^{(j)}$
denoting its length. The matrix
![]() $\unicode[STIX]{x1D648}$
accounts for both the weights
$\unicode[STIX]{x1D648}$
accounts for both the weights
![]() $\unicode[STIX]{x1D652}(\boldsymbol{x})$
and numerical quadrature weights stemming from the spatial integration in (2.7). The matrices
$\unicode[STIX]{x1D652}(\boldsymbol{x})$
and numerical quadrature weights stemming from the spatial integration in (2.7). The matrices
![]() $\unicode[STIX]{x1D731}=[\unicode[STIX]{x1D719}^{(1)}(\boldsymbol{x},t),\unicode[STIX]{x1D719}^{(2)}(\boldsymbol{x},t),\ldots ,\unicode[STIX]{x1D719}^{(N_{peaks})}(\boldsymbol{x},t)]$
and
$\unicode[STIX]{x1D731}=[\unicode[STIX]{x1D719}^{(1)}(\boldsymbol{x},t),\unicode[STIX]{x1D719}^{(2)}(\boldsymbol{x},t),\ldots ,\unicode[STIX]{x1D719}^{(N_{peaks})}(\boldsymbol{x},t)]$
and
![]() $\unicode[STIX]{x1D726}=\text{diag}[\unicode[STIX]{x1D706}^{(1)},\unicode[STIX]{x1D706}^{(2)},\ldots ,\unicode[STIX]{x1D706}^{(N_{peaks})}]$
contain the eigenvectors and eigenvalues, i.e. space–time POD modes and their corresponding energies in the space–time inner product, respectively. In practice, the large eigenvalue problem (2.8) is solved by computing the cheaper eigendecomposition of the smaller matrix
$\unicode[STIX]{x1D726}=\text{diag}[\unicode[STIX]{x1D706}^{(1)},\unicode[STIX]{x1D706}^{(2)},\ldots ,\unicode[STIX]{x1D706}^{(N_{peaks})}]$
contain the eigenvectors and eigenvalues, i.e. space–time POD modes and their corresponding energies in the space–time inner product, respectively. In practice, the large eigenvalue problem (2.8) is solved by computing the cheaper eigendecomposition of the smaller matrix
![]() $\unicode[STIX]{x1D64C}^{\ast }\unicode[STIX]{x1D648}\unicode[STIX]{x1D64C}$
first, in the same manner as for standard POD (Sirovich Reference Sirovich1987). Note that the eigenvectors
$\unicode[STIX]{x1D64C}^{\ast }\unicode[STIX]{x1D648}\unicode[STIX]{x1D64C}$
first, in the same manner as for standard POD (Sirovich Reference Sirovich1987). Note that the eigenvectors
![]() $\unicode[STIX]{x1D753}(\boldsymbol{x},t)$
of the space–time correlation tensor that constitute the conditional space–time POD modes are dependent on time. In contrast, classical and spectral POD modes are functions of space only. By construction, space–time POD modes are coherent in space and over the time horizon
$\unicode[STIX]{x1D753}(\boldsymbol{x},t)$
of the space–time correlation tensor that constitute the conditional space–time POD modes are dependent on time. In contrast, classical and spectral POD modes are functions of space only. By construction, space–time POD modes are coherent in space and over the time horizon
![]() $\unicode[STIX]{x0394}T$
, and orthogonal in the space–time inner product (2.5).
$\unicode[STIX]{x0394}T$
, and orthogonal in the space–time inner product (2.5).
3 Example: acoustic bursts in a round supersonic jet
As an example, we consider acoustic bursts that are intermittently emitted from a high-Reynolds-number round jet and tailor the space–time inner product (2.5) as well as the event
![]() $H$
to this application. A total of 10 000 snapshots separated by
$H$
to this application. A total of 10 000 snapshots separated by
![]() $\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}t^{\ast }c_{\infty }/D=0.1$
acoustical time units of a high-fidelity LES by Brès et al. (Reference Brès, Ham, Nichols and Lele2017) of a heated ideally expanded turbulent jet with jet Mach number
$\unicode[STIX]{x0394}t=\unicode[STIX]{x0394}t^{\ast }c_{\infty }/D=0.1$
acoustical time units of a high-fidelity LES by Brès et al. (Reference Brès, Ham, Nichols and Lele2017) of a heated ideally expanded turbulent jet with jet Mach number
![]() $M_{j}=U_{j}/c_{j}=1.5$
, Reynolds number
$M_{j}=U_{j}/c_{j}=1.5$
, Reynolds number
![]() $Re=\unicode[STIX]{x1D70C}_{j}U_{j}D/\unicode[STIX]{x1D707}_{j}=$
155 000 and nozzle temperature ratio
$Re=\unicode[STIX]{x1D70C}_{j}U_{j}D/\unicode[STIX]{x1D707}_{j}=$
155 000 and nozzle temperature ratio
![]() $T_{0}/T_{\infty }=2.53$
are analysed. A wall model was used to describe the turbulent boundary layer inside the nozzle (not part of the cylindrical domain considered below). The subscripts
$T_{0}/T_{\infty }=2.53$
are analysed. A wall model was used to describe the turbulent boundary layer inside the nozzle (not part of the cylindrical domain considered below). The subscripts
![]() $j$
,
$j$
,
![]() $\infty$
and
$\infty$
and
![]() $0$
indicate jet, stagnation and free-stream conditions, the superscript
$0$
indicate jet, stagnation and free-stream conditions, the superscript
![]() $\ast$
marks dimensional quantities,
$\ast$
marks dimensional quantities,
![]() $c$
is the speed of sound,
$c$
is the speed of sound,
![]() $T$
the temperature,
$T$
the temperature,
![]() $\unicode[STIX]{x1D707}$
the dynamic viscosity and
$\unicode[STIX]{x1D707}$
the dynamic viscosity and
![]() $D$
the nozzle diameter. The data for our study correspond to the pressure field of case
$D$
the nozzle diameter. The data for our study correspond to the pressure field of case
![]() $A2$
in Brès et al. (Reference Brès, Ham, Nichols and Lele2017), and the reader is referred to that paper for more details. For cylindrical coordinates with
$A2$
in Brès et al. (Reference Brès, Ham, Nichols and Lele2017), and the reader is referred to that paper for more details. For cylindrical coordinates with
![]() $\boldsymbol{x}=(x,r)$
and
$\boldsymbol{x}=(x,r)$
and
![]() $\text{d}V=r\,\text{d}\,x\,\text{d}r$
, where
$\text{d}V=r\,\text{d}\,x\,\text{d}r$
, where
![]() $x$
and
$x$
and
![]() $r$
are the streamwise and radial coordinates, respectively, the rotational symmetry allows for a Fourier decomposition of the pressure field
$r$
are the streamwise and radial coordinates, respectively, the rotational symmetry allows for a Fourier decomposition of the pressure field
into azimuthal Fourier modes
![]() $\hat{\boldsymbol{p}}_{m}(x,r,t)$
. For our demonstration, we focus on the
$\hat{\boldsymbol{p}}_{m}(x,r,t)$
. For our demonstration, we focus on the
![]() $m=1$
component of the data as shown in figure 1, which contains the largest fraction of the fluctuating energy of unheated jets (Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018). In the following, we drop the
$m=1$
component of the data as shown in figure 1, which contains the largest fraction of the fluctuating energy of unheated jets (Schmidt et al.
Reference Schmidt, Towne, Rigas, Colonius and Brès2018). In the following, we drop the
![]() $\hat{(\cdot )}_{1}$
with the understanding that
$\hat{(\cdot )}_{1}$
with the understanding that
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $p$
denote the
$p$
denote the
![]() $m=1$
Fourier component of the pressure. The pressure 2-norm
$m=1$
Fourier component of the pressure. The pressure 2-norm
is chosen as a convenient measure for the acoustic energy of the flow.
In order to focus on the acoustic emissions into the far field plus the outer part of the shear layer, we choose
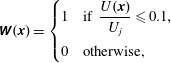 $$\begin{eqnarray}\unicode[STIX]{x1D652}(\boldsymbol{x})=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\frac{U(\boldsymbol{x})}{U_{j}}\leqslant 0.1,\\ 0\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D652}(\boldsymbol{x})=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\frac{U(\boldsymbol{x})}{U_{j}}\leqslant 0.1,\\ 0\quad & \text{otherwise,}\end{array}\right.\end{eqnarray}$$
to mask out the highly energetic pressure fluctuations in the jet column. Here,
![]() $U$
is the mean streamwise velocity and
$U$
is the mean streamwise velocity and
![]() $U_{j}$
the jet velocity. The threshold
$U_{j}$
the jet velocity. The threshold
![]() $U(\boldsymbol{x})\leqslant 0.1U_{j}$
, i.e. the region outside the green lines in figure 1(b,c), is chosen as a suitable way to distinguish these different parts of the flow. The inclusion of the outer part of the shear layer facilitates backtracking of the acoustic burst event to its precursor in the mixing region close to the nozzle. The final results were found to be qualitatively independent of the exact choice of thresholding.
$U(\boldsymbol{x})\leqslant 0.1U_{j}$
, i.e. the region outside the green lines in figure 1(b,c), is chosen as a suitable way to distinguish these different parts of the flow. The inclusion of the outer part of the shear layer facilitates backtracking of the acoustic burst event to its precursor in the mixing region close to the nozzle. The final results were found to be qualitatively independent of the exact choice of thresholding.
The event
![]() $H$
is specified to identify loud events, or acoustic bursts, in the far field of the jet. In particular, we detect such events as local maxima in time from a single-point measurement of the far-field pressure
$H$
is specified to identify loud events, or acoustic bursts, in the far field of the jet. In particular, we detect such events as local maxima in time from a single-point measurement of the far-field pressure
![]() $p(\boldsymbol{x}_{0},t)$
at some probe location
$p(\boldsymbol{x}_{0},t)$
at some probe location
![]() $\boldsymbol{x}_{0}=(x_{0},r_{0})$
. For the case at hand, we detect loud events at
$\boldsymbol{x}_{0}=(x_{0},r_{0})$
. For the case at hand, we detect loud events at
![]() $(x_{0},r_{0})=(12,5)$
, see figure 1. This location corresponds to the peak location of the power spectral density of the pressure along the edge of the domain, i.e. the dominant aft-angle noise. A local maximum that identifies an event is said to be detected at time
$(x_{0},r_{0})=(12,5)$
, see figure 1. This location corresponds to the peak location of the power spectral density of the pressure along the edge of the domain, i.e. the dominant aft-angle noise. A local maximum that identifies an event is said to be detected at time
![]() $t_{0}$
if
$t_{0}$
if
![]() $|p(\boldsymbol{x}_{0},t_{0})|$
is larger than its two neighbouring samples at
$|p(\boldsymbol{x}_{0},t_{0})|$
is larger than its two neighbouring samples at
![]() $t=t_{0}-\unicode[STIX]{x0394}t$
and
$t=t_{0}-\unicode[STIX]{x0394}t$
and
![]() $t=t_{0}+\unicode[STIX]{x0394}t$
in discrete time. The event is hence defined as
$t=t_{0}+\unicode[STIX]{x0394}t$
in discrete time. The event is hence defined as
where
![]() $t_{sim}=[\unicode[STIX]{x0394}t,2\unicode[STIX]{x0394}t,\ldots ,10^{4}\unicode[STIX]{x0394}t]$
is the set of discrete simulation times at which the LES snapshots have been saved. We further restrict the conditional expectation
$t_{sim}=[\unicode[STIX]{x0394}t,2\unicode[STIX]{x0394}t,\ldots ,10^{4}\unicode[STIX]{x0394}t]$
is the set of discrete simulation times at which the LES snapshots have been saved. We further restrict the conditional expectation
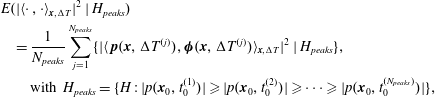 $$\begin{eqnarray}\displaystyle & & \displaystyle E(|\langle \cdot \,,\cdot \rangle _{\boldsymbol{x},\unicode[STIX]{x0394}T}|^{2}\mid H_{peaks})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N_{peaks}}\mathop{\sum }_{j=1}^{N_{peaks}}\{|\langle \,\boldsymbol{p}(\boldsymbol{x},\unicode[STIX]{x0394}T^{(j)}),\unicode[STIX]{x1D753}(\boldsymbol{x},\unicode[STIX]{x0394}T^{(j)})\rangle _{\boldsymbol{ x},\unicode[STIX]{x0394}T}|^{2}\mid H_{peaks}\},\nonumber\\ \displaystyle & & \displaystyle \qquad \text{with }H_{peaks}=\{H:|p(\boldsymbol{x}_{0},t_{0}^{(1)})|\geqslant |p(\boldsymbol{x}_{0},t_{0}^{(2)})|\geqslant \cdots \geqslant |p(\boldsymbol{x}_{0},t_{0}^{(N_{peaks})})|\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle E(|\langle \cdot \,,\cdot \rangle _{\boldsymbol{x},\unicode[STIX]{x0394}T}|^{2}\mid H_{peaks})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{N_{peaks}}\mathop{\sum }_{j=1}^{N_{peaks}}\{|\langle \,\boldsymbol{p}(\boldsymbol{x},\unicode[STIX]{x0394}T^{(j)}),\unicode[STIX]{x1D753}(\boldsymbol{x},\unicode[STIX]{x0394}T^{(j)})\rangle _{\boldsymbol{ x},\unicode[STIX]{x0394}T}|^{2}\mid H_{peaks}\},\nonumber\\ \displaystyle & & \displaystyle \qquad \text{with }H_{peaks}=\{H:|p(\boldsymbol{x}_{0},t_{0}^{(1)})|\geqslant |p(\boldsymbol{x}_{0},t_{0}^{(2)})|\geqslant \cdots \geqslant |p(\boldsymbol{x}_{0},t_{0}^{(N_{peaks})})|\},\end{eqnarray}$$
sorted such that the first
![]() $N_{peaks}$
largest peaks are selected, i.e. we threshold the cardinality
$N_{peaks}$
largest peaks are selected, i.e. we threshold the cardinality
![]() $|H|$
of the event.
$|H|$
of the event.
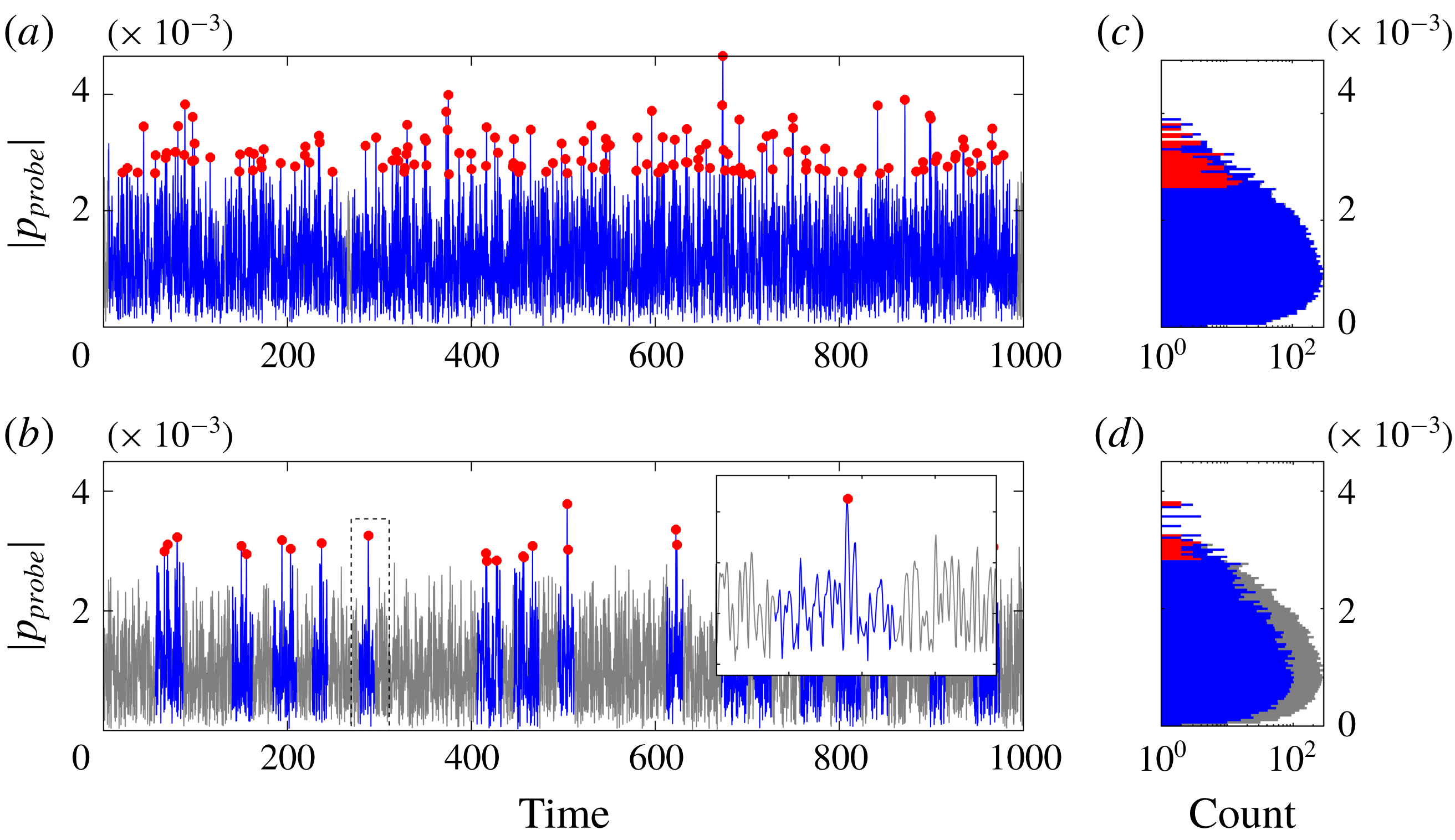
Figure 2. Time trace (a,b) and histogram (c,d) of the pressure at the probe location
![]() $(x_{0},r_{0})=(12,5)$
: (a,c)
$(x_{0},r_{0})=(12,5)$
: (a,c)
![]() $m=1$
component with
$m=1$
component with
![]() $t^{-}=150\unicode[STIX]{x0394}t$
and
$t^{-}=150\unicode[STIX]{x0394}t$
and
![]() $t^{+}=149\unicode[STIX]{x0394}t$
, such that
$t^{+}=149\unicode[STIX]{x0394}t$
, such that
![]() $\unicode[STIX]{x0394}T=30$
spans
$\unicode[STIX]{x0394}T=30$
spans
![]() $300$
snapshots centred about any
$300$
snapshots centred about any
![]() $t_{0}^{(j)}$
, and
$t_{0}^{(j)}$
, and
![]() $N_{peaks}=200$
; (b,d)
$N_{peaks}=200$
; (b,d)
![]() $m=1$
component with
$m=1$
component with
![]() $t^{-}=100\unicode[STIX]{x0394}t$
,
$t^{-}=100\unicode[STIX]{x0394}t$
,
![]() $t^{+}=60\unicode[STIX]{x0394}t$
,
$t^{+}=60\unicode[STIX]{x0394}t$
,
![]() $N_{peaks}=35$
. The insert in (b) shows an example of an isolated event. The full signal is shown in grey; red symbols pinpoint events that occur at times
$N_{peaks}=35$
. The insert in (b) shows an example of an isolated event. The full signal is shown in grey; red symbols pinpoint events that occur at times
![]() $t_{0}^{(j)},$
with blue signals to indicate their temporal neighbourhoods
$t_{0}^{(j)},$
with blue signals to indicate their temporal neighbourhoods
![]() $t_{0}^{(j)}-t^{-}\leqslant \unicode[STIX]{x0394}T^{(j)}\leqslant t_{0}^{(j)}+t^{+}$
.
$t_{0}^{(j)}-t^{-}\leqslant \unicode[STIX]{x0394}T^{(j)}\leqslant t_{0}^{(j)}+t^{+}$
.
Figure 2 shows the time trace of the pressure signal at the probe location and its histogram for two different choices of space–time POD parameters
![]() $t^{-}$
,
$t^{-}$
,
![]() $t^{+}$
, and
$t^{+}$
, and
![]() $N_{peaks}$
. The parameter combination
$N_{peaks}$
. The parameter combination
![]() $t^{-}=150$
,
$t^{-}=150$
,
![]() $t^{+}=149$
, and
$t^{+}=149$
, and
![]() $N_{peaks}=200$
shown in figure 2(a,c) is used in the remainder of this paper. This choice centres the extreme event within a time interval of
$N_{peaks}=200$
shown in figure 2(a,c) is used in the remainder of this paper. This choice centres the extreme event within a time interval of
![]() $30$
acoustic units, which approximates the time it takes an acoustic pulse to transverse the domain. The combination shown in figure 2(b,d) solely serves as a less dense example, with the insert highlighting a single isolated event (filled red circle) occurring at
$30$
acoustic units, which approximates the time it takes an acoustic pulse to transverse the domain. The combination shown in figure 2(b,d) solely serves as a less dense example, with the insert highlighting a single isolated event (filled red circle) occurring at
![]() $t_{0}=288.1$
and its temporal neighbourhood, or time segment,
$t_{0}=288.1$
and its temporal neighbourhood, or time segment,
![]() $278.1\leqslant \unicode[STIX]{x0394}T\leqslant 294.6$
(blue line segment). Note that every snapshot might well contain multiple extreme events at different stages of their temporal evolution, which results in overlapping time segments. The plots in figure 2(c,d) use the same colour representation as used for the time trace to distinguish the histogram of the entire signal (grey) from those of the event (red) and segments (blue). As we are considering the absolute value of a presumingly Gaussian-distributed random signal, the time trace histogram can be approximated by a
$278.1\leqslant \unicode[STIX]{x0394}T\leqslant 294.6$
(blue line segment). Note that every snapshot might well contain multiple extreme events at different stages of their temporal evolution, which results in overlapping time segments. The plots in figure 2(c,d) use the same colour representation as used for the time trace to distinguish the histogram of the entire signal (grey) from those of the event (red) and segments (blue). As we are considering the absolute value of a presumingly Gaussian-distributed random signal, the time trace histogram can be approximated by a
![]() $\unicode[STIX]{x1D712}^{2}$
-distribution. By the definition of
$\unicode[STIX]{x1D712}^{2}$
-distribution. By the definition of
![]() $H$
in (3.4), the extreme acoustic events occupy the tail of this distribution.
$H$
in (3.4), the extreme acoustic events occupy the tail of this distribution.
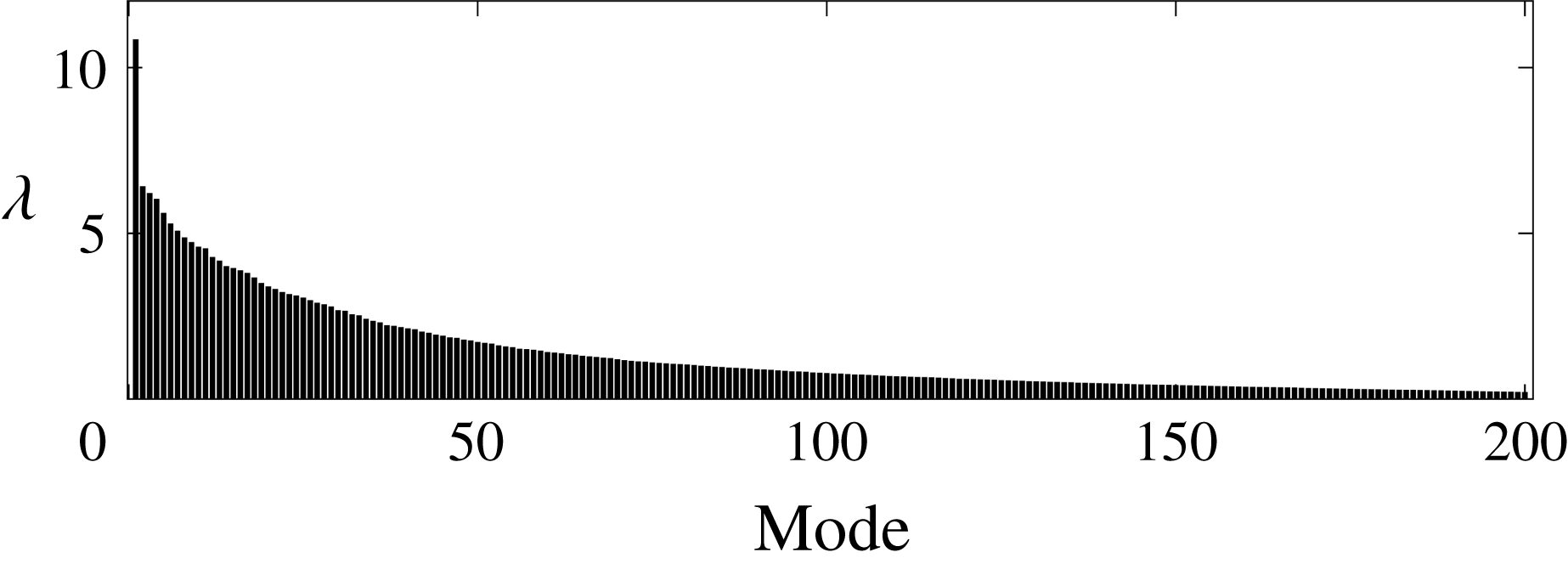
Figure 3. Conditional space–time POD energy spectrum for
![]() $t^{-}=150\unicode[STIX]{x0394}t$
,
$t^{-}=150\unicode[STIX]{x0394}t$
,
![]() $t^{+}=149\unicode[STIX]{x0394}t$
and
$t^{+}=149\unicode[STIX]{x0394}t$
and
![]() $N_{peaks}=200$
.
$N_{peaks}=200$
.
In figure 3, we present the eigenvalue, or energy spectrum of the conditional space–time POD problem defined by the parameters presented in figure 2(a,c). Two features of the spectrum stand out: (i) the dominance of the principal eigenvalue, which is
![]() ${\approx}40\,\%$
larger than the following eigenvalue; (ii) the slow decay of the rest of the spectrum, starting with the second mode. These two observations are crucial to our analysis as they indicate that the particular space–time structure associated with the first eigenvalue plays a dominant role in the space–time statistics.
${\approx}40\,\%$
larger than the following eigenvalue; (ii) the slow decay of the rest of the spectrum, starting with the second mode. These two observations are crucial to our analysis as they indicate that the particular space–time structure associated with the first eigenvalue plays a dominant role in the space–time statistics.

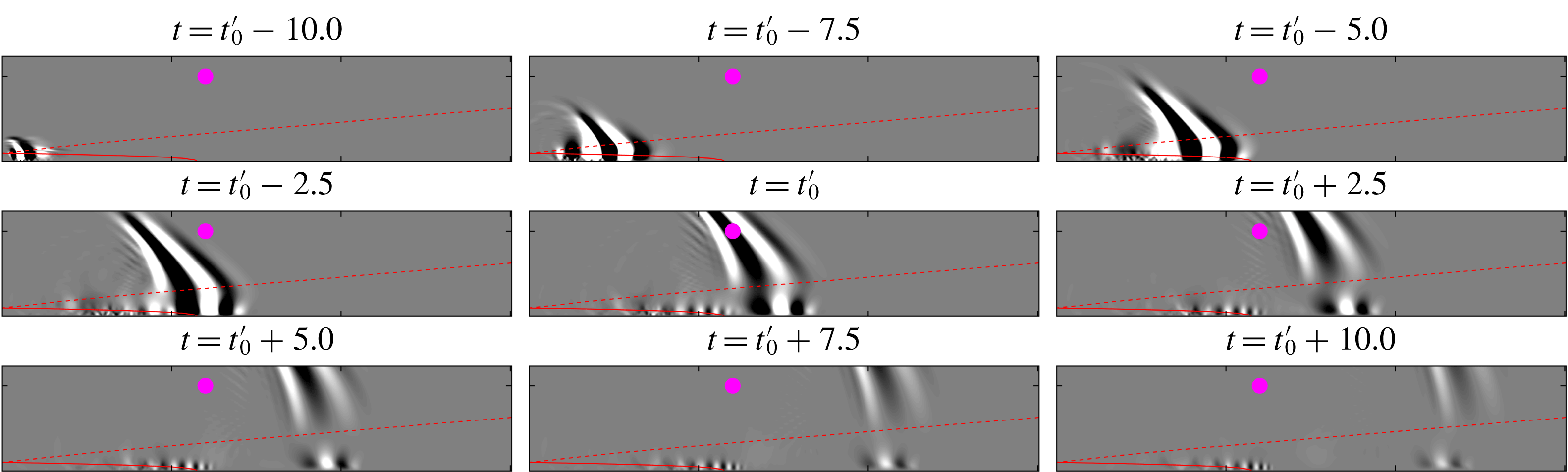
Figure 4. Temporal evolution of the leading conditional space–time POD mode (
We next investigate the corresponding structure, i.e. the leading space–time POD mode
![]() $\unicode[STIX]{x1D719}^{(1)}(\boldsymbol{x},t)$
, in figure 4. Nine representative time instances
$\unicode[STIX]{x1D719}^{(1)}(\boldsymbol{x},t)$
, in figure 4. Nine representative time instances
![]() $t^{(j)}=[50\unicode[STIX]{x0394}T,75\unicode[STIX]{x0394}T,100\unicode[STIX]{x0394}T,\ldots ,250\unicode[STIX]{x0394}T]$
that track the event’s evolution from its formation in the near-nozzle shear layer (top left) to the time it exits the computational domain (lower right) are shown. The first instance at
$t^{(j)}=[50\unicode[STIX]{x0394}T,75\unicode[STIX]{x0394}T,100\unicode[STIX]{x0394}T,\ldots ,250\unicode[STIX]{x0394}T]$
that track the event’s evolution from its formation in the near-nozzle shear layer (top left) to the time it exits the computational domain (lower right) are shown. The first instance at
![]() $t=t_{0}-10$
represents the earliest time for which we observe a distinct localized wavepacket structure. This structure is identified as the initial seed, or precursor, of the acoustic burst, and over time evolves into an acoustic burst with a distinct wavenumber, spatial extent and ejection angle. The existence of a statistically prevalent mode was a priori not obvious, and suggests the existence of an underlying physical mechanism.
$t=t_{0}-10$
represents the earliest time for which we observe a distinct localized wavepacket structure. This structure is identified as the initial seed, or precursor, of the acoustic burst, and over time evolves into an acoustic burst with a distinct wavenumber, spatial extent and ejection angle. The existence of a statistically prevalent mode was a priori not obvious, and suggests the existence of an underlying physical mechanism.
Motivated by a number of studies that demonstrate that mean flow stability analysis can yield accurate predictions of the dynamics of turbulent flows (see, for example, Beneddine et al.
Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016), we seek a description of the average linear burst event in terms of its linear dynamics, here represented by the compressible Navier–Stokes operator
![]() $\unicode[STIX]{x1D63C}=\unicode[STIX]{x1D63C}(\overline{\boldsymbol{q}},\boldsymbol{x},m)$
linearized about the mean state
$\unicode[STIX]{x1D63C}=\unicode[STIX]{x1D63C}(\overline{\boldsymbol{q}},\boldsymbol{x},m)$
linearized about the mean state
![]() $\overline{\boldsymbol{q}}$
. In absence of a model for the effective Reynolds number in mean flow stability analyses, and as in Schmidt et al. (Reference Schmidt, Towne, Rigas, Colonius and Brès2018), we let
$\overline{\boldsymbol{q}}$
. In absence of a model for the effective Reynolds number in mean flow stability analyses, and as in Schmidt et al. (Reference Schmidt, Towne, Rigas, Colonius and Brès2018), we let
![]() $Re=3\times 10^{4}$
. The reader is referred to the latter reference for a more detailed discussion and for details of the discretization, which omits the nozzle. The optimality of the conditional POD formulation in the space–time inner product leads itself to an optimal transient growth problem
$Re=3\times 10^{4}$
. The reader is referred to the latter reference for a more detailed discussion and for details of the discretization, which omits the nozzle. The optimality of the conditional POD formulation in the space–time inner product leads itself to an optimal transient growth problem
that maximizes the growth of energy as measured in the spatial inner product
![]() $\langle \boldsymbol{q}_{1},\boldsymbol{q}_{2}\rangle _{E}=\int _{V}\boldsymbol{q}_{1}^{\ast }(\boldsymbol{x})\,\unicode[STIX]{x1D652}^{\prime }(\boldsymbol{x})\,\boldsymbol{q}_{2}(\boldsymbol{x})\,\text{d}V$
and over a finite time
$\langle \boldsymbol{q}_{1},\boldsymbol{q}_{2}\rangle _{E}=\int _{V}\boldsymbol{q}_{1}^{\ast }(\boldsymbol{x})\,\unicode[STIX]{x1D652}^{\prime }(\boldsymbol{x})\,\boldsymbol{q}_{2}(\boldsymbol{x})\,\text{d}V$
and over a finite time
![]() $\unicode[STIX]{x1D70F}=t^{-}+t^{+}$
. Here,
$\unicode[STIX]{x1D70F}=t^{-}+t^{+}$
. Here,
![]() $\unicode[STIX]{x1D652}^{\prime }(\boldsymbol{x})$
contains the same spatial restriction given by (3.3) as before and, in addition, the component-wise weights of the compressible energy norm first introduced by Chu (Reference Chu1965).
$\unicode[STIX]{x1D652}^{\prime }(\boldsymbol{x})$
contains the same spatial restriction given by (3.3) as before and, in addition, the component-wise weights of the compressible energy norm first introduced by Chu (Reference Chu1965).
![]() $\mathscr{A}(\unicode[STIX]{x1D70F})=\text{e}^{\unicode[STIX]{x1D63C}\unicode[STIX]{x1D70F}}$
represents the evolution operator that maps
$\mathscr{A}(\unicode[STIX]{x1D70F})=\text{e}^{\unicode[STIX]{x1D63C}\unicode[STIX]{x1D70F}}$
represents the evolution operator that maps
![]() $\boldsymbol{q}(0)$
onto
$\boldsymbol{q}(0)$
onto
![]() $\boldsymbol{q}(\unicode[STIX]{x1D70F})$
, and
$\boldsymbol{q}(\unicode[STIX]{x1D70F})$
, and
![]() $\mathscr{A}^{\dagger }(\unicode[STIX]{x1D70F})=\text{e}^{\unicode[STIX]{x1D63C}^{\ast }\unicode[STIX]{x1D70F}}$
is defined as its adjoint counterpart that maps
$\mathscr{A}^{\dagger }(\unicode[STIX]{x1D70F})=\text{e}^{\unicode[STIX]{x1D63C}^{\ast }\unicode[STIX]{x1D70F}}$
is defined as its adjoint counterpart that maps
![]() $\boldsymbol{q}^{\dagger }(\unicode[STIX]{x1D70F})$
onto
$\boldsymbol{q}^{\dagger }(\unicode[STIX]{x1D70F})$
onto
![]() $\boldsymbol{q}^{\dagger }(0)$
back in time. As in Schmidt et al. (Reference Schmidt, Hosseini, Rist, Hanifi and Henningson2015), we converge the initial condition
$\boldsymbol{q}^{\dagger }(0)$
back in time. As in Schmidt et al. (Reference Schmidt, Hosseini, Rist, Hanifi and Henningson2015), we converge the initial condition
![]() $\boldsymbol{q}(0)$
by direct-adjoint looping, and enforce the spatial restriction implied by (3.3) at the beginning of each iteration. A comprehensive review of non-modal theory can be found in Schmid (Reference Schmid2007).
$\boldsymbol{q}(0)$
by direct-adjoint looping, and enforce the spatial restriction implied by (3.3) at the beginning of each iteration. A comprehensive review of non-modal theory can be found in Schmid (Reference Schmid2007).
The time evolution of the pressure component of the optimal initial condition
![]() $\boldsymbol{q}(0)$
is reported in figure 5. The gain associated with this optimal structure, as defined in (3.6), is
$\boldsymbol{q}(0)$
is reported in figure 5. The gain associated with this optimal structure, as defined in (3.6), is
![]() $G(\unicode[STIX]{x1D70F})=231$
. The waves in the end region of the potential core are described in detail by Tam & Hu (Reference Tam and Hu1989) and Towne et al. (Reference Towne, Cavalieri, Jordan, Colonius, Schmidt, Jaunet and Brès2017), and are not relevant for this study. The time offset
$G(\unicode[STIX]{x1D70F})=231$
. The waves in the end region of the potential core are described in detail by Tam & Hu (Reference Tam and Hu1989) and Towne et al. (Reference Towne, Cavalieri, Jordan, Colonius, Schmidt, Jaunet and Brès2017), and are not relevant for this study. The time offset
![]() $t_{0}^{\prime }=40$
aligns the evolution of the optimal structure with that of the leading conditional space–time POD mode depicted in figure 4, and is introduced without loss of generality as we are interested in the evolution relative to the occurrence of an event at the probe location. A remarkable correspondence between the optimal structure and the dominant space–time POD mode is observed. This correspondence strongly suggests that non-modal, transient growth plays a critical role in the generation of the average acoustic burst event. The close correspondence at early times in particular, suggests that the precursor takes the form of the optimal initial condition, which in turn corresponds to the adjoint solution
$t_{0}^{\prime }=40$
aligns the evolution of the optimal structure with that of the leading conditional space–time POD mode depicted in figure 4, and is introduced without loss of generality as we are interested in the evolution relative to the occurrence of an event at the probe location. A remarkable correspondence between the optimal structure and the dominant space–time POD mode is observed. This correspondence strongly suggests that non-modal, transient growth plays a critical role in the generation of the average acoustic burst event. The close correspondence at early times in particular, suggests that the precursor takes the form of the optimal initial condition, which in turn corresponds to the adjoint solution
![]() $\boldsymbol{q}^{\dagger }(0)=\boldsymbol{q}(0)$
. This suggests that an acoustic burst is triggered whenever turbulent fluctuations randomly align with the theoretical optimal initial condition, i.e. if their projection onto the adjoint is large. In this scenario, the associated gain is then more appropriately interpreted as a sensitivity of output perturbations with appreciable amplitudes to small-amplitude initial disturbances.
$\boldsymbol{q}^{\dagger }(0)=\boldsymbol{q}(0)$
. This suggests that an acoustic burst is triggered whenever turbulent fluctuations randomly align with the theoretical optimal initial condition, i.e. if their projection onto the adjoint is large. In this scenario, the associated gain is then more appropriately interpreted as a sensitivity of output perturbations with appreciable amplitudes to small-amplitude initial disturbances.
4 Conclusions
We present a data-driven approach based on a conditional space–time POD formulation that is tailored to the eduction and statistical description of intermittent or rare events from data. The resulting modes are orthonormal in a space–time inner product and optimally capture the conditional variance of an ensemble of realizations of the intermittent event. By construction, the modes are coherent in space and over a finite time horizon. The formalism hence bridges the gap between standard POD modes, which are coherent at zero time lag only, and spectral POD modes, which are perfectly coherent over all time.
It can also be thought of as an extension to classical time-resolved conditional averaging that has previously been applied as a structure identification technique, for example to identify acoustic source locations in jets (Guj et al. Reference Guj, Carley, Camussi and Ragni2003), or more recently to examine the hairpin generation process in turbulent wall boundary layers (Hack & Moin Reference Hack and Moin2018). Compared to conditional averaging, the method introduced here has the additional advantage that it inherits the desirable mathematical properties from the POD formalism.
To demonstrate the approach, we apply conditional space–time POD to the example of Mach wave radiation of a turbulent jet. We find a statistically dominant space–time mode that is energetically well separated from all other modes. It takes the form of a spatially confined wavepacket that originates in the thin initial shear layer close to the nozzle. Over time, this initial seed evolves into an acoustic burst of a distinct wavenumber and spatial support that is emitted into the far field. The structure and dynamics of this prototype acoustic burst suggest the existence of an underlying physical mechanism. We investigate the possibility of optimal transient growth as a candidate mechanism, and find a remarkable agreement between the evolution of the optimal initial condition and the leading POD mode.
The orthogonality and optimality properties of the conditional space–time POD modes make them potential candidates for basis functions for use in reduced-order models of transient processes. In fluid mechanics, Galerkin models (see, for example, Noack, Morzynski & Tadmor Reference Noack, Morzynski and Tadmor2011) are widely successful and build on exactly these properties. The temporal coherence of the modes furthermore enables the identification of precursors of extreme events, such as the initial seed of the acoustic burst event shown in the first panel of figure 4. We plan to leverage this capability for model-predictive control in the future.
Acknowledgements
We gratefully acknowledge support during the 2018 Summer Program at the Center for Turbulence Research at Stanford University where this work was initiated. O.T.S. thanks T. Colonius and gratefully acknowledges support from the Office of Naval Research under grant no. N00014-16-1-2445 with Dr K. Millsaps as program manager for the portion of the work that was completed at Caltech. Thanks are due to A. Towne, S. Lele and S. L. Smith for fruitful discussions and valuable comments. The LES study was supported by the NAVAIR SBIR project, under the supervision of Dr J. T. Spyropoulos. The main LES calculations were carried out on CRAY XE6 machines at DoD HPC facilities in ERDC DSRC.
Supplementary movie
Supplementary movie is available at https://doi.org/10.1017/jfm.2019.200.