No CrossRef data available.
Published online by Cambridge University Press: 10 June 2019
The release of buoyant harmful gases within enclosed spaces, such as tunnels and corridors, may engender specific health, industrial and transportation risks. For safety, a simple ventilation strategy for these spaces is to impose a flow along the tunnel, whose velocity is defined as ‘critical’, that confines the front of harmful buoyant gases immediately downstream of the source of emission. Determining the critical velocity as a function of the geometrical and dynamical conditions at the source is a fundamental fluid mechanics problem which has yet to be elucidated; this problem concerns the dynamics of non-Boussinesq releases relating to large differences between the densities of the buoyant and the ambient fluids. We have investigated this problem theoretically, by means of a simplified model of a top-hat plume in a cross-flow, and in complementary experiments by means of tests in a reduced-scale ventilated tunnel, examining releases from circular sources. Experimental results reveal: (i) the existence of two flow regimes depending on the plume Richardson number at the source 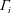 $\unicode[STIX]{x1D6E4}_{i}$, one for momentum-dominated releases,
$\unicode[STIX]{x1D6E4}_{i}$, one for momentum-dominated releases, 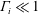 $\unicode[STIX]{x1D6E4}_{i}\ll 1$, and a second for buoyancy-dominated releases,
$\unicode[STIX]{x1D6E4}_{i}\ll 1$, and a second for buoyancy-dominated releases, 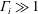 $\unicode[STIX]{x1D6E4}_{i}\gg 1$, with a smooth transition between the two; and (ii) the presence of relevant non-Boussinesq effects only for momentum-dominated releases. All these features can be conveniently predicted by the plume-based model, whose validity is, strictly speaking, limited to releases issuing from ‘small’ sources in ‘weak’ ventilation flows. Analytical solutions of the model are generally in good agreement with the experimental data, even for values of the governing parameters that are beyond the range of validity for the model. The solutions aid to clarify the effect of the source radius, and reveal interesting behaviours in the limits
$\unicode[STIX]{x1D6E4}_{i}\gg 1$, with a smooth transition between the two; and (ii) the presence of relevant non-Boussinesq effects only for momentum-dominated releases. All these features can be conveniently predicted by the plume-based model, whose validity is, strictly speaking, limited to releases issuing from ‘small’ sources in ‘weak’ ventilation flows. Analytical solutions of the model are generally in good agreement with the experimental data, even for values of the governing parameters that are beyond the range of validity for the model. The solutions aid to clarify the effect of the source radius, and reveal interesting behaviours in the limits 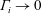 $\unicode[STIX]{x1D6E4}_{i}\rightarrow 0$ and
$\unicode[STIX]{x1D6E4}_{i}\rightarrow 0$ and 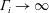 $\unicode[STIX]{x1D6E4}_{i}\rightarrow \infty$. These findings support the adoption of simplified models to simulate light gas releases in confined ventilated spaces.
$\unicode[STIX]{x1D6E4}_{i}\rightarrow \infty$. These findings support the adoption of simplified models to simulate light gas releases in confined ventilated spaces.