Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T10:57:02.225Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of viscous instability by variation of injection rate in a fluid with time-dependent rheology

Published online by Cambridge University Press:  14 September 2017

Tim H. Beeson-Jones Open the ORCID record for Tim H. Beeson-Jones [Opens in a new window]  and
Andrew W. Woods Open the ORCID record for Andrew W. Woods [Opens in a new window]
Tim H. Beeson-Jones
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: aww1@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Using variational calculus, we investigate the time-dependent injection rate that minimises the growth of the Saffman–Taylor instability when a finite volume of fluid is injected in a finite time, 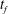$t_{f}$, into a Hele-Shaw cell. We first consider a planar interface, and show that, with a constant viscosity ratio, the constant injection rate is optimal. When the viscosity of the displacing fluid, 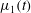$\unicode[STIX]{x1D707}_{1}(t)$, gradually increases over time, as may occur with a slowly gelling polymer solution, the optimal injection rate, 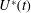$U^{\ast }(t)$, involves a gradual increase in the flow rate with time. This leads to a smaller initial value of flow rate than the constant injection rate, finishing with a larger value. Such optimisation can lead to a substantial suppression of the instability as compared to the constant injection case if the characteristic gelling time is comparable to 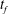$t_{f}$. In contrast, for either relatively slow or fast gelling, there is much less benefit in selecting the optimal injection rate, 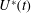$U^{\ast }(t)$, as compared to the constant injection rate. In the case of a constant injection rate from a point source, 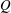$Q$, then with a constant viscosity ratio the fastest-growing perturbation on the radially spreading front involves axisymmetric modes whose wavenumber increases with time. Approximating the discrete azimuthal modes by a continuous distribution, we find the injection rate that minimises growth, 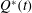$Q^{\ast }(t)$. We find that there is a critical time for injection, 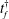$t_{f}^{\dagger }$, such that if 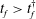$t_{f}>t_{f}^{\dagger }$ then 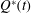$Q^{\ast }(t)$ can be chosen so that the interface is always stable. This critical time emerges from the case with an injection rate given by 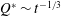$Q^{\ast }\sim t^{-1/3}$. As the total injection time is reduced to values 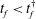$t_{f}<t_{f}^{\dagger }$, the system becomes progressively more unstable, and the optimal injection rate for an idealised continuous distribution of azimuthal modes asymptotes to a flow rate that increases linearly with time. As for the one-dimensional case, if the viscosity of the injection fluid gradually increases over time, then the optimal injection rate has a smaller initial value but gradually increases to larger values than for the analogous constant viscosity problem. If the displacing fluid features shear-thinning rheology, then the optimal injection rate involves a smaller flow rate at early times, although not as large a reduction as in the Newtonian case, and a larger flow rate at late times, although not as large an increase as in the Newtonian case.

JFM classification

Low-Reynolds-number flows: Hele-Shaw flows Flow Control: Instability control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 829 , 25 October 2017 , pp. 214 - 235
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Housseiny, T. T. & Stone, H. A. 2013 Controlling viscous fingering in tapered Hele-Shaw cells. Phys. Fluids 25, 092102.Google Scholar
Aronsson, G. & Janfalk, U. 1992 On Hele-Shaw flow of power-law fluids. Eur. J. Appl. Maths 3 (4), 343–366.CrossRefGoogle Scholar
Batista, C., Dias, E. O. & Miranda, J. A. 2016 Hamiltonian formulation towards minimization of viscous fluid fingering. Phys. Rev. E 94 (1), 013109.Google ScholarPubMed
Beeson-Jones, T. H. & Woods, A. W. 2015 On the selection of viscosity to suppress the Saffman–Taylor instability in a radially spreading annulus. J. Fluid Mech. 782, 127–143.Google Scholar
Cardoso, S. S. S. & Woods, A. W. 1995 The formation of drops through viscous instability. J. Fluid Mech. 289, 351–378.Google Scholar
Chen, C. Y. & Yan, P. Y. 2017 Radial flows in heterogeneous porous media with a linear injection scheme. Comput. Fluids 142, 30–36.Google Scholar
Dias, E. O., Alvarez-Lacalle, E., Carvalho, M. S. & Miranda, J. A. 2012 Minimization of viscous fluid fingering: a variational scheme for optimal flow rates. Phys. Rev. Lett. 109 (14), 144502.CrossRefGoogle ScholarPubMed
Dias, E. O. & Miranda, J. A. 2010 Control of radial fingering patterns: a weakly nonlinear approach. Phys. Rev. E 81 (1), 016312.Google Scholar
Dias, E. O., Parisio, F. & Miranda, J. A. 2010 Suppression of viscous fluid fingering: a piecewise-constant injection process. Phys. Rev. E 82 (6), 067301.Google ScholarPubMed
Fontana, J. V., Dias, E. O. & Miranda, J. A. 2014 Controlling and minimizing fingering instabilities in non-Newtonian fluids. Phys. Rev. E 89 (1), 013016.Google Scholar
Ghannam, M. & Esmail, M. 1998 Rheological properties of aqueous polyacrylamide solutions. J. Appl. Polym. Sci. 69 (8), 1587–1597.Google Scholar
Gin, C. & Daripa, P. 2015 Stability results for multi-layer radial Hele-Shaw and porous media flows. Phys. Fluids 27, 012101.Google Scholar
Gorell, S. & Homsy, G. M. 1983 A theory of optimal policy of oil recovery by secondary displacement processes. SIAM J. Appl. Maths 43, 79–98.Google Scholar
Gun, W. J & Routh, A. F. 2013 Microcapsule flow behaviour in porous media. Chem. Engng Sci. 102, 309–314.Google Scholar
Han, M, Shi, L., Ye, M & Ma, J. 1995 Crosslinking reaction of polyacrylamide with chromium(III). Polym. Bull. 35, 109–113.Google Scholar
Huang, Y. S. & Chen, C. Y. 2015 A numerical study on radial Hele-Shaw flow: influence of fluid miscibility and injection scheme. Comput. Mech. 55 (2), 407–420.Google Scholar
Kamal, M. S., Sultan, A. S., Al-Mubaiyedh, U. A. & Hussein, I. A. 2015 Review on polymer flooding: rheology, adsorption, stability, and field applications of various polymer systems. Polym. Rev. 55 (3), 491–530.Google Scholar
Lake, L. W. 1989 Enhanced Oil Recovery. Prentice-Hall.Google Scholar
Lee, K. E., Morad, N., Teng, T. T. & Poh, B. T. 2012 Kinetics and in situ rheological behavior of acrylamide redox polymerization. J. Dispersion Sci. Technol. 33 (3), 387–395.Google Scholar
Li, S., Lowengrub, J., Fontana, J. & Palffy-Muhoray, P. 2009 Control of viscous fingering patterns in a radial Hele-Shaw cell. Phys. Rev. Lett. 102 (17), 174501.Google Scholar
Makadia, H. K. & Siegel, S. J. 2011 Poly lactic-co-glycolic acid (PLGA) as biodegradable controlled drug delivery carrier. Polymers 3 (3), 1377–1397.Google Scholar
Martyushev, L. M., Birzina, A. I., Konovalov, M. S. & Sergeev, A. P. 2015 Morphological stability of an interface between two non-Newtonian fluids moving in a Hele-Shaw cell. Phys. Rev. E 80, 066306.Google Scholar
McCue, S. W. & King, J. R. 2011 Contracting bubbles in Hele-Shaw cells with a power-law fluid. Nonlinearity 24, 613–641.Google Scholar
Mora, S. & Manna, M. 2009 Saffman–Taylor instability for generalized Newtonian fluids. Phys. Rev. E 80 (1), 016308.Google ScholarPubMed
Paterson, L. 1981 Radial fingering in a Hele-Shaw cell. J. Fluid Mech. 113, 513–539.Google Scholar
Pihler-Puzović, D., Illien, P., Heil, M. & Juel, A. 2012 Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 108 (7), 074502.Google Scholar
Praud, O. & Swinney, H. L. 2005 Fractal dimension and unscreened angles measured for radial viscous fingering. Phys. Rev. E 72 (1), 011406.Google Scholar
Sader, J. E., Chan, D. Y. C. & Hughes, B. D. 1994 Non-Newtonian effects on immiscible viscous fingering in a radial Hele-Shaw cell. Phys. Rev. E 49 (1), 420–433.Google Scholar
Saffman, P. G. & Taylor, G. I. 1958 The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. J. Fluid Mech. 245, 312–329.Google Scholar
Sorbie, K. 1991 Polymer-Improved Oil Recovery. CRC Press.Google Scholar
Tran-viet, A., Routh, A. F. & Woods, A. W. 2014 Control of the permeability of a porous media using a thermally sensitive polymer. Am. Inst. Chem. Engrs 60 (3), 1193–1201.Google Scholar
Wilson, S. D. R. 1990 The Taylor–Saffman problem for a non-Newtonian liquid. J. Fluid Mech. 220, 413–425.Google Scholar
Woods, A. W. 2015 Flow in Porous Media. Cambridge University Press.Google Scholar
Zheng, Z., Kim, H. & Stone, H. A. 2015 Controlling viscous fingering using time-dependent strategies. Phys. Rev. Lett. 115 (17), 174501.CrossRefGoogle ScholarPubMed