Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-23T21:47:59.968Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergent Richtmyer–Meshkov instability of a heavy gas layer with perturbed outer interface

Published online by Cambridge University Press:  06 September 2019

Juchun Ding Open the ORCID record for Juchun Ding [Opens in a new window] ,
Jianming Li ,
Rui Sun ,
Zhigang Zhai Open the ORCID record for Zhigang Zhai [Opens in a new window]  and
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]
Juchun Ding
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Jianming Li
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Rui Sun
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Zhigang Zhai
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
Xisheng Luo*
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei 230026, China
*
†Email address for correspondence: xluo@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

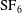The evolution of an $\text{SF}_{6}$ layer surrounded by air is experimentally studied in a semi-annular convergent shock tube by high-speed schlieren photography. The gas layer with a sinusoidal outer interface and a circular inner interface is realized by the soap-film technique such that the initial condition is well controlled. Results show that the thicker the gas layer, the weaker the interface–coupling effect and the slower the evolution of the outer interface. Induced by the distorted transmitted shock and the interface coupling, the inner interface exhibits a slow perturbation growth which can be largely suppressed by reducing the layer thickness. After the reshock, the inner perturbation increases linearly at a growth rate independent of the initial layer thickness as well as of the outer perturbation amplitude and wavelength, and the growth rate can be well predicted by the model of Mikaelian (Physica D, vol. 36, 1989, pp. 343–357) with an empirical coefficient of 0.31. After the linear stage, the growth rate decreases continuously, and finally the perturbation freezes at a constant amplitude caused by the successive stagnation of spikes and bubbles. The convergent geometry constraint as well as the very weak compressibility at late stages are responsible for this instability freeze-out.

JFM classification

Compressible Flows: Shock waves Mixing: Turbulent mixing Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 878 , 10 November 2019 , pp. 277 - 291
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bell, G. I.1951 Taylor instability on cylinders and spheres in the small amplitude approximation. LANL Rep. No. LA-1321.Google Scholar
Budzinski, J. M., Benjamin, R. F. & Jacobs, J. W. 1994 Influence of initial conditions on the flow patters of a shock-accelerated thin fluid layer. Phys. Fluids 6, 3510–3512.Google Scholar
Ding, J., Si, T., Yang, J., Lu, X., Zhai, Z. & Luo, X. 2017 Measurement of a Richtmyer–Meshkov instability at an air–SF6 interface in a semiannular shock tube. Phys. Rev. Lett. 119 (1), 014501.Google Scholar
Henry de Frahan, M. T., Movahed, P. & Johnsen, E. 2015 Numerical simulations of a shock interacting with successive interfaces using the discontinuous Galerkin method: the multilayered Richtmyer–Meshkov and Rayleigh–Taylor instabilities. Shock Waves 25 (4), 329–345.Google Scholar
Hosseini, S. H. R. & Takayama, K. 2005 Experimental study of Richtmyer–Meshkov instability induced by cylndrical shock waves. Phys. Fluids 17, 084101.Google Scholar
Jacobs, J. W., Krivets, V. V. & Tsiklashvili, V. 2013 Experiments on the Richtmyer–Meshkov instability with an imposed, random initial perturbation. Shock Waves 23, 407–413.Google Scholar
Lei, F., Ding, J., Si, T., Zhai, Z. & Luo, X. 2017 Experimental study on a sinusoidal air/SF6 interface accelerated by a cylindrically converging shock. J. Fluid Mech. 826, 819–829.Google Scholar
Leinov, E., Malamud, G., Elbaz, Y., Levin, L. A., Ben-Dor, G., Shvarts, D. & Sadot, O. 2009 Experimental and numerical investigation of the Richtmyer–Meshkov instability under re-shock conditions. J. Fluid Mech. 626, 449–475.Google Scholar
Lindl, J., Landen, O., Edwards, J., Moses, E. & Team, N. 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21, 020501.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014 Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth. J. Fluid Mech. 748, 85–112.Google Scholar
Luo, X., Ding, J., Wang, M., Zhai, Z. & Si, T. 2015 A semi-annular shock tube for studying cylindrically converging Richtmyer–Meshkov instability. Phys. Fluids 27 (9), 091702.Google Scholar
Luo, X., Zhang, F., Ding, J., Si, T., Yang, J., Zhai, Z. & Wen, C. 2018 Long-term effect of Rayleigh–Taylor stabilization on converging Richtmyer–Meshkov instability. J. Fluid Mech. 849, 231–244.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4, 101–104.Google Scholar
Mikaelian, K. O. 1989 Turbulent mixing generated by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Physica D 36, 343–357.Google Scholar
Mikaelian, K. O. 1995 Rayleigh–Taylor and Richtmyer–Meshkov instabilities in finite-thickness fluid layers. Phys. Fluids 7 (4), 888–890.Google Scholar
Mikaelian, K. O. 2005 Rayleigh–Taylor and Richtmyer–Meshkov instabilities and mixing in stratified cylindrical shells. Phys. Fluids 17, 094105.Google Scholar
Ranjan, D., Niederhaus, J. H. J., Oakley, J. G., Anderson, M. H., Bonazza, R. & Greenough, J. A. 2008 Shock-bubble interactions: features of divergent shock-refraction geometry observed in experiments and simulations. Phys. Fluids 20, 036101.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 13, 297–319.Google Scholar
Tomkins, C. D., Balakumar, B. J., Orlicz, G., Prestridge, K. P. & Ristorcelli, J. R. 2013 Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence. J. Fluid Mech. 735, 288–306.Google Scholar
Ukai, S., Balakrishnan, K. & Menon, S. 2011 Growth rate predictions of single- and multi-mode Richtmyer–Meshkov instability with reshock. Shock Waves 21, 533–546.Google Scholar
Vandenboomgaerde, M., Rouzier, P., Souffland, D., Biamino, L., Jourdan, G., Houas, L. & Mariani, C. 2018 Nonlinear growth of the converging Richtmyer–Meshkov instability in a conventional shock tube. Phys. Rev. Fluids 3, 014001.Google Scholar
Zhai, Z., Liang, Y., Liu, L., Ding, J., Luo, X. & Zou, L. 2018 Interaction of rippled shock wave with flat fast-slow interface. Phys. Fluids 30 (4), 046104.Google Scholar
Zhai, Z., Liu, C., Qin, F., Yang, J. & Luo, X. 2010 Generation of cylindrical converging shock waves based on shock dynamcis theory. Phys. Fluids 22, 041701.Google Scholar
Zou, L., Liu, J., Liao, S., Zheng, X., Zhai, Z. & Luo, X. 2017 Richtmyer–Meshkov instability of a flat interface subjected to a rippled shock wave. Phys. Rev. E 95, 013107.Google Scholar