Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-23T22:56:41.669Z Has data issue: false hasContentIssue false
  • English
  • Français

The critical point of the transition to turbulence in pipe flow

Published online by Cambridge University Press:  25 January 2018

Vasudevan Mukund  and
Björn Hof Open the ORCID record for Björn Hof [Opens in a new window]
Vasudevan Mukund
Affiliation:
IST Austria, Am Campus 1, 3400 Klosterneuburg, Austria
Björn Hof*
Affiliation:
IST Austria, Am Campus 1, 3400 Klosterneuburg, Austria
*
†Email address for correspondence: bhof@ist.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

In pipes, turbulence sets in despite the linear stability of the laminar Hagen–Poiseuille flow. The Reynolds number (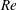$Re$) for which turbulence first appears in a given experiment – the ‘natural transition point’ – depends on imperfections of the set-up, or, more precisely, on the magnitude of finite amplitude perturbations. At onset, turbulence typically only occupies a certain fraction of the flow, and this fraction equally is found to differ from experiment to experiment. Despite these findings, Reynolds proposed that after sufficiently long times, flows may settle to steady conditions: below a critical velocity, flows should (regardless of initial conditions) always return to laminar, while above this velocity, eddying motion should persist. As will be shown, even in pipes several thousand diameters long, the spatio-temporal intermittent flow patterns observed at the end of the pipe strongly depend on the initial conditions, and there is no indication that different flow patterns would eventually settle to a (statistical) steady state. Exploiting the fact that turbulent puffs do not age (i.e. they are memoryless), we continuously recreate the puff sequence exiting the pipe at the pipe entrance, and in doing so introduce periodic boundary conditions for the puff pattern. This procedure allows us to study the evolution of the flow patterns for arbitrary long times, and we find that after times in excess of 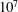$10^{7}$ advective time units, indeed a statistical steady state is reached. Although the resulting flows remain spatio-temporally intermittent, puff splitting and decay rates eventually reach a balance, so that the turbulent fraction fluctuates around a well-defined level which only depends on 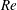$Re$. In accordance with Reynolds’ proposition, we find that at lower 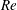$Re$ (here 2020), flows eventually always resume to laminar, while for higher 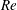$Re$ (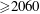${\geqslant}2060$), turbulence persists. The critical point for pipe flow hence falls in the interval of 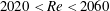$2020<Re<2060$, which is in very good agreement with the recently proposed value of 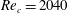$Re_{c}=2040$. The latter estimate was based on single-puff statistics and entirely neglected puff interactions. Unlike in typical contact processes where such interactions strongly affect the percolation threshold, in pipe flow, the critical point is only marginally influenced. Interactions, on the other hand, are responsible for the approach to the statistical steady state. As shown, they strongly affect the resulting flow patterns, where they cause ‘puff clustering’, and these regions of large puff densities are observed to travel across the puff pattern in a wave-like fashion.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent transition
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 76 - 94
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.CrossRefGoogle ScholarPubMed
Avila, M., Willis, A. P. & Hof, B. 2010 On the transient nature of localized pipe flow turbulence. J. Fluid Mech. 646, 127–136.Google Scholar
Barkley, D. 2011 Simplifying the complexity of pipe flow. Phys. Rev. E 84 (1), 016309.Google ScholarPubMed
Barkley, D. 2016 Theoretical perspective on the route to turbulence in a pipe. J. Fluid Mech. 803, P1.CrossRefGoogle Scholar
Barkley, D., Song, B., Mukund, V., Lemoult, G., Avila, M. & Hof, B. 2015 The rise of fully turbulent flow. Nature 526 (7574), 550–553.CrossRefGoogle ScholarPubMed
Binnie, A. M. 1945 A double-refraction method of detecting turbulence in liquids. Proc. Phys. Soc. 57 (5), 390–402.CrossRefGoogle Scholar
Binnie, A. M. & Fowler, J. S. 1947 A study by a double-refraction method of the development of turbulence in a long circular tube. Proc. R. Soc. Lond. A 192, 32–44.Google Scholar
Bottin, S. & Chaté, H. 1998 Statistical analysis of the transition to turbulence in plane Couette flow. Eur. Phys. J. B 6 (1), 143–155.Google Scholar
Bottin, S., Daviaud, F., Manneville, P. & Dauchot, O. 1998 Discontinuous transition to spatiotemporal intermittency in plane Couette flow. Europhys. Lett. 43 (2), 171.Google Scholar
Brosa, U. 1989 Turbulence without strange attractor. J. Stat. Phys. 55 (5–6), 1303–1312.Google Scholar
Chaté, H. & Manneville, P. 1988 Spatio-temporal intermittency in coupled map lattices. Phys. D 32 (3), 409–422.Google Scholar
Faisst, H. & Eckhardt, B. 2004 Sensitive dependence on initial conditions in transition to turbulence in pipe flow. J. Fluid Mech. 504, 343–352.CrossRefGoogle Scholar
Grassberger, P. 1982 On phase transitions in Schlögl’s second model. Z. für Phys. B 47 (4), 365–374.Google Scholar
Hinrichsen, H. 2000 Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49 (7), 815–958.Google Scholar
Hof, B., de Lozar, A., Avila, M., Tu, X. & Schneider, T. M. 2010 Eliminating turbulence in spatially intermittent flows. Science 327 (5972), 1491–1494.CrossRefGoogle ScholarPubMed
Hof, B., de Lozar, A., Kuik, D. J. & Westerweel, J. 2008 Repeller or attractor? Selecting the dynamical model for the onset of turbulence in pipe flow. Phys. Rev. Lett. 101 (21), 214501.CrossRefGoogle ScholarPubMed
Hof, B., Westerweel, J., Schneider, T. M. & Eckhardt, B. 2006 Finite lifetime of turbulence in shear flows. Nature 443 (7107), 59–62.CrossRefGoogle ScholarPubMed
Janssen, H.-K. 1981 On the nonequilibrium phase transition in reaction–diffusion systems with an absorbing stationary state. Z. für Phys. B 42 (2), 151–154.Google Scholar
Kaneko, K. 1985 Spatiotemporal intermittency in coupled map lattices. Prog. Theor. Phys. 74 (5), 1033–1044.Google Scholar
Kuik, D. J., Poelma, C. & Westerweel, J. 2010 Quantitative measurement of the lifetime of localized turbulence in pipe flow. J. Fluid Mech. 645, 529.CrossRefGoogle Scholar
Lemoult, G., Shi, L., Avila, K., Jalikop, S. V., Avila, M. & Hof, B. 2016 Directed percolation phase transition to sustained turbulence in Couette flow. Nat. Phys. 12 (3), 254–258.CrossRefGoogle Scholar
Lindgren, E. R. 1953 Some aspects of the change between laminar and turbulent flow of liquids in cylindrical tubes. Ark. Fys. 7 (23), 293–308.Google Scholar
de Lozar, A. & Hof, B. 2009 An experimental study of the decay of turbulent puffs in pipe flow. Phil. Trans. R. Soc. Lond. A 367 (1888), 589–599.Google ScholarPubMed
Manneville, P. 2015 On the transition to turbulence of wall-bounded flows in general, and plane Couette flow in particular. Eur. J. Mech. (B/Fluids) 49, 345–362.Google Scholar
Meseguer, A. & Trefethen, L. N. 2003 Linearized pipe flow to Reynolds number 107 . J. Comput. Phys. 186 (1), 178–197.Google Scholar
Moxey, D. & Barkley, D. 2010 Distinct large-scale turbulent–laminar states in transitional pipe flow. Proc. Natl Acad. Sci. USA 107 (18), 8091–8096.Google Scholar
Pavelyev, A. A., Reshmin, A. I., Teplovodskii, S. Kh. & Fedoseev, S. G. 2003 On the lower critical Reynolds number for flow in a circular pipe. Fluid Dyn. 38 (4), 545–551.CrossRefGoogle Scholar
Pavelyev, A. A., Reshmin, A. I. & Trifonov, V. V. 2006 Effect of the pattern of initial perturbations on the steady pipe flow regime. Fluid Dyn. 41 (6), 916–922.CrossRefGoogle Scholar
Peixinho, J. & Mullin, T. 2006 Decay of turbulence in pipe flow. Phys. Rev. Lett. 96 (9), 094501.Google Scholar
Pomeau, Y. 1986 Front motion, metastability and subcritical bifurcations in hydrodynamics. Phys. D 23 (1), 3–11.Google Scholar
Reynolds, O. 1884 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. A 174, 935–982.Google Scholar
Reynolds, O. 1895 On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Phil. Trans. R. Soc. Lond. A 186, 123–164.Google Scholar
von Rotta, J. 1956 Experimenteller Beitrag zur Entstehung turbulenter Strömung im Rohr. Arch. Appl. Mech. 24 (4), 258–281.Google Scholar
Samanta, D., De Lozar, A. & Hof, B. 2011 Experimental investigation of laminar turbulent intermittency in pipe flow. J. Fluid Mech. 681, 193–204.Google Scholar
Sano, M. & Tamai, K. 2016 A universal transition to turbulence in channel flow. Nat. Phys. 12 (3), 249–253.Google Scholar
Schiller, L. 1921 Experimentelle Untersuchungen zum Turbulenzproblem. Z. Angew. Math. Mech.-J. Appl. Math. Mech. 1 (6), 436–444.Google Scholar
Sibulkin, M. 1962 Transition from turbulent to laminar pipe flow. Phys. Fluids 5 (3), 280–284.Google Scholar
Stern, E. 1970 Beitrag zur Untersuchung der Intermittenz einer Rohrströmung. Acta Mech. 10 (1–2), 67–84.Google Scholar
Willis, A. P. & Kerswell, R. R. 2007 Critical behavior in the relaminarization of localized turbulence in pipe flow. Phys. Rev. Lett. 98 (1), 014501.CrossRefGoogle ScholarPubMed
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59 (02), 281–335.Google Scholar
Xiong, X., Tao, J., Chen, S. & Brandt, L. 2015 Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers. Phys. Fluids 27 (4), 041702.Google Scholar