Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-24T14:24:58.580Z Has data issue: false hasContentIssue false
  • English
  • Français

Data-driven construction of a reduced-order model for supersonic boundary layer transition

Published online by Cambridge University Press:  15 July 2019

Ming Yu Open the ORCID record for Ming Yu [Opens in a new window] ,
Wei-Xi Huang Open the ORCID record for Wei-Xi Huang [Opens in a new window]  and
Chun-Xiao Xu Open the ORCID record for Chun-Xiao Xu [Opens in a new window]
Ming Yu
Affiliation:
Key Laboratory of Applied Mechanics (AML), Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Wei-Xi Huang
Affiliation:
Key Laboratory of Applied Mechanics (AML), Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
Chun-Xiao Xu*
Affiliation:
Key Laboratory of Applied Mechanics (AML), Department of Engineering Mechanics, Tsinghua University, Beijing 100084, PR China
*
†Email address for correspondence: xucx@tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, a data-driven method for the construction of a reduced-order model (ROM) for complex flows is proposed. The method uses the proper orthogonal decomposition (POD) modes as the orthogonal basis and the dynamic mode decomposition method to obtain linear equations for the temporal evolution coefficients of the modes. This method eliminates the need for the governing equations of the flows involved, and therefore saves the effort of deriving the projected equations and proving their consistency, convergence and stability, as required by the conventional Galerkin projection method, which has been successfully applied to incompressible flows but is hard to extend to compressible flows. Using a sparsity-promoting algorithm, the dimensionality of the ROM is further reduced to a minimum. 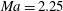The ROMs of the natural and bypass transitions of supersonic boundary layers at $Ma=2.25$ are constructed by the proposed data-driven method. The temporal evolution of the POD modes shows good agreement with that obtained by direct numerical simulations in both cases.

JFM classification

Compressible Flows: Compressible boundary layers Nonlinear Dynamical Systems: Low-dimensional models Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 1096 - 1114
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balajewicz, M., Tezaur, I. & Dowell, E. 2016 Minimal subspace rotation on the Stiefel manifold for stabilization and enhancement of projection-based reduced order models for the compressible Navier–Stokes equations. J. Comput. Phys. 321, 224–241.10.1016/j.jcp.2016.05.037Google Scholar
Barone, M. F., Kalashnikova, I., Segalman, D. J. & Thornquist, H. K. 2009 Stable Galerkin reduced order models for linearized compressible flow. J. Comput. Phys. 228 (6), 1932–1946.10.1016/j.jcp.2008.11.015Google Scholar
Duriez, T., Brunton, S. L. & Noack, B. R. 2017 Machine Learning Control – Taming Nonlinear Dynamics and Turbulence. Springer International.10.1007/978-3-319-40624-4Google Scholar
Gloerfelt, X. 2008 Compressible proper orthogonal decomposition/Galerkin reduced-order model of self-sustained oscillations in a cavity. Phys. Fluids 20 (11), 115105.10.1063/1.2998448Google Scholar
Holmes, P., Lumley, J. L., Berkooz, G. & Rowley, C. W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.10.1017/CBO9780511919701Google Scholar
Ilak, M. & Rowley, C. W. 2008 Modeling of transitional channel flow using balanced proper orthogonal decomposition. Phys. Fluids 20 (3), 034103.10.1063/1.2840197Google Scholar
Jovanović, M. R., Schmid, P. J. & Nichols, J. W. 2014 Sparsity-promoting dynamic mode decomposition. Phys. Fluids 26 (2), 024103.10.1063/1.4863670Google Scholar
Kalashnikova, I., Arunajatesan, S., Barone, M. F., van Bloemen Waanders, B. G. & Fike, J. A.2014a Reduced order modeling for prediction and control of large-scale systems. Report, SAND, (2014-4693). Sandia National Laboratories.10.2172/1177206Google Scholar
Kalashnikova, I. & Barone, M. F. 2010 On the stability and convergence of a Galerkin reduced order model (ROM) of compressible flow with solid wall and far-field boundary treatment. Intl J. Numer. Meth. Engng 83 (10), 1345–1375.10.1002/nme.2867Google Scholar
Kalashnikova, I., Barone, M. F., Arunajatesan, S. & van Bloemen Waanders, B. G. 2014b Construction of energy-stable projection-based reduced order models. Appl. Maths Comput. 249, 569–596.10.1016/j.amc.2014.10.073Google Scholar
Kutz, J. N., Fu, X. & Brunton, S. L. 2016 Multiresolution dynamic mode decomposition. SIAM J. Appl. Dyn. Syst. 15 (2), 713–735.10.1137/15M1023543Google Scholar
Li, X. L., Fu, D. X., Ma, Y. W. & Liang, X. 2010 Direct numerical simulation of compressible turbulent flows. Acta Mechanica Sin. 26 (6), 795–806.10.1007/s10409-010-0394-8Google Scholar
Lumley, J. L. & Poje, A. 1997 Low-dimensional models for flows with density fluctuations. Phys. Fluids 9 (7), 2023–2031.10.1063/1.869321Google Scholar
Noack, B. R., Papas, P. & Monkewitz, P. A. 2005 The need for a pressure-term representation in empirical Galerkin models of incompressible shear flows. J. Fluid Mech. 523, 339–365.10.1017/S0022112004002149Google Scholar
Noack, B. R., Stankiewicz, W., Morzyński, M. & Schmid, P. J. 2016 Recursive dynamic mode decomposition of transient and post-transient wake flows. J. Fluid Mech. 809, 843–872.10.1017/jfm.2016.678Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at M = 2. 25. Phys. Fluids 16 (3), 530–545.10.1063/1.1637604Google Scholar
Rowley, C. W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15 (03), 997–1013.10.1142/S0218127405012429Google Scholar
Rowley, C. W., Colonius, T. & Murray, R. M. 2004 Model reduction for compressible flows using POD and Galerkin projection. Physica D: Nonlinear Phenomena 189 (1–2), 115–129.10.1016/j.physd.2003.03.001Google Scholar
Rowley, C. W. & Dawson, S. T. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.10.1146/annurev-fluid-010816-060042Google Scholar
Sayadi, T., Schmid, P. J., Nichols, J. W. & Moin, P. 2014 Reduced-order representation of near-wall structures in the late transitional boundary layer. J. Fluid Mech. 748, 278–301.10.1017/jfm.2014.184Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.10.1017/S0022112010001217Google Scholar
Smith, T. R.2003 Low-dimensional models of plane Couette flow using the proper orthogonal decomposition. PhD thesis, Princeton University.Google Scholar
Subbareddy, P. K., Bartkowicz, M. D. & Candler, G. V. 2014 Direct numerical simulation of high-speed transition due to an isolated roughness element. J. Fluid Mech. 748, 848–878.10.1017/jfm.2014.204Google Scholar