Hostname: page-component-6b989bf9dc-pkhfk Total loading time: 0 Render date: 2024-04-14T20:49:38.160Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagnosing mixing in stratified turbulent flows with a locally defined available potential energy

Published online by Cambridge University Press:  06 January 2014

Alberto Scotti  and
Brian White
Alberto Scotti*
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
Brian White
Affiliation:
Department of Marine Sciences, University of North Carolina, Chapel Hill, NC 27599, USA
*
†Email address for correspondence: ascotti@unc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A local available potential energy (APE) density useful as suitable diagnostic tool in turbulent stratified flows is considered under the Boussinesq approximation. The local APE is positive, and in the limit of infinitesimal perturbation from an equilibrium state recovers the Lorenz energy cycle definition of APE. In a turbulent stratified flow, the APE can be Reynolds-decomposed into non-trivial mean and turbulent components, which are connected to the mean and turbulent kinetic energy by suitably defined fluxes. 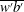We show that the turbulent buoyancy flux $\overline{w'b'}$ and the rate of production of turbulent APE coincide only under very special circumstances. The framework is applied to derive some global bounds on the mixing efficiency of some representative flows.

JFM classification

Mixing: Mixing Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Geophysical and Geological Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 740 , 10 February 2014 , pp. 114 - 135
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G. 1981 A note on potential energy density in a stratified compressible fluid. J. Fluid Mech. 107, 227–236.CrossRefGoogle Scholar
Asai, T. 1970 Stability of a plane parallel flow with variable vertical shear and unstable stratification. J. Met. Soc. Japan 48 (2), 129–138.Google Scholar
Ellison, T. H. 1957 Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech. 2, 456–466.Google Scholar
Gnanadesikan, A., Slater, R. D., Swathi, P. S. & Vallis, G. K. 2005 The energetics of ocean heat transport. J. Climate 18, 2604–2616.CrossRefGoogle Scholar
Holliday, D. & McIntyre, M. E. 1981 On potential energy density in an incompressible stratified fluid. J. Fluid Mech. 107, 221–225.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Lamb, K. 2007 Energy and pseudoenergy flux in the internal wave field generated by tidal flow over topography. Cont. Shelf Res. 27 (9), 1208–1232.CrossRefGoogle Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167.CrossRefGoogle Scholar
Margules, M. 1903 Über die Energie der Stürme. Jahrb. Zent.-Anst. Meteorol. Erdmagnet. 48, 1–26.Google Scholar
Molemaker, M. J. & McWilliams, J. C. 2010 Local balance and cross-scale flux of available potential energy. J. Fluid Mech. 645, 295–314.Google Scholar
Oort, A. H., Anderson, L. A. & Peixoto, J. P. 1994 Estimates of the energy cycle of the oceans. J. Geophys. Res. 99 (C4), 7665–7688.Google Scholar
Roullet, G. & Klein, P. 2009 Available potential energy diagnosis in a direct numerical simulation of rotating stratified turbulence. J. Fluid Mech. 624, 45–55.Google Scholar
Rudin, W. 1987 Real and Complex Analysis. McGraw-Hill.Google Scholar
IIScotti, A. 2005 Orographic effects during winter cold-air outbreaks over the Sea of Japan (East Sea): results from a shallow-layer model. Deep-Sea Res. 52, 1705–1725.Google Scholar
Scotti, A., Beardsley, R. & Butman, B. 2006 On the interpretation of energy and energy fluxes of nonlinear internal waves: an example from Massachusetts Bay. J. Fluid Mech. 561, 103–112.Google Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really ‘non turbulent’?. Geophys. Res. Lett. 38, L21609.Google Scholar
Shepherd, T. G. 1993 A unified theory of available potential-energy. Atmos.-Ocean 31, 1–26.CrossRefGoogle Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
von Storch, J.-S., Carsten, E., Fast, I., Haak, H., Hernàndez-Deckers, D., Maier-Reimer, E., Marotzke, J. & Stammer, D. 2012 An estimate of the Lorenz energy cycle for the World Ocean based on the $1/10^0$ STORM/NCEP simulation. J. Phys. Oceanogr. 42, 2185–2205.Google Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.Google Scholar
Tailleux, R. G. J. 2013 Available potential energy and exergy in stratified fluids. Annu. Rev. Fluid Mech. 45, 35–58.Google Scholar
Tennekes, H. & Lumley, J. L. 1989 A First Course in Turbulence. MIT Press.Google Scholar
Tseng, Y.-H. & Ferziger, J. H. 2001 Mixing and available potential energy in stratified flows. Phys. Fluids 13 (5), 1281–1293.Google Scholar
Winters, K. B. & Barkan, R. 2012 Available potential energy density for Boussinesq fluid flow. J. Fluid Mech. 714, 476–488.CrossRefGoogle Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar