Article contents
Diffusiophoresis, Batchelor scale and effective Péclet numbers
Published online by Cambridge University Press: 08 August 2019
Abstract
We study the joint mixing of colloids and salt released together in a stagnation point or in a globally chaotic flow. In the presence of salt inhomogeneities, the mixing time is strongly modified depending on the sign of the diffusiophoretic coefficient 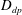 $D_{dp}$. Mixing is delayed when
$D_{dp}$. Mixing is delayed when 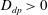 $D_{dp}>0$ (salt-attracting configuration), or faster when
$D_{dp}>0$ (salt-attracting configuration), or faster when 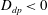 $D_{dp}<0$ (salt-repelling configuration). In both configurations, as for molecular diffusion alone, large scales are barely affected in the dilating direction while the Batchelor scale for the colloids,
$D_{dp}<0$ (salt-repelling configuration). In both configurations, as for molecular diffusion alone, large scales are barely affected in the dilating direction while the Batchelor scale for the colloids, 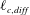 $\ell _{c,diff}$, is strongly modified by diffusiophoresis. We propose here to measure a global effect of diffusiophoresis in the mixing process through an effective Péclet number built on this modified Batchelor scale. Whilst this small scale is obtained analytically for the stagnation point, in the case of chaotic advection, we derive it using the equation of gradients of concentration, following Raynal & Gence (Intl J. Heat Mass Transfer, vol. 40 (14), 1997, pp. 3267–3273). Comparing to numerical simulations, we show that the mixing time can be predicted by using the same function as in absence of salt, but as a function of the effective Péclet numbers computed for each configuration. The approach is shown to be valid when the ratio
$\ell _{c,diff}$, is strongly modified by diffusiophoresis. We propose here to measure a global effect of diffusiophoresis in the mixing process through an effective Péclet number built on this modified Batchelor scale. Whilst this small scale is obtained analytically for the stagnation point, in the case of chaotic advection, we derive it using the equation of gradients of concentration, following Raynal & Gence (Intl J. Heat Mass Transfer, vol. 40 (14), 1997, pp. 3267–3273). Comparing to numerical simulations, we show that the mixing time can be predicted by using the same function as in absence of salt, but as a function of the effective Péclet numbers computed for each configuration. The approach is shown to be valid when the ratio 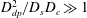 $D_{dp}^{2}/D_{s}D_{c}\gg 1$, where
$D_{dp}^{2}/D_{s}D_{c}\gg 1$, where 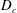 $D_{c}$ and
$D_{c}$ and 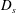 $D_{s}$ are the diffusivities of the colloids and salt.
$D_{s}$ are the diffusivities of the colloids and salt.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 14
- Cited by

