Published online by Cambridge University Press: 29 April 2013
The onset and development of turbulence from controlled disturbances in compressible (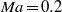 $\mathit{Ma}= 0. 2$), flat-plate boundary layers is studied by direct numerical simulation. We have validated the initial disturbance development, confirmed that H- and K-regime transitions were reproduced and, from these starting points, we carried these simulations beyond breakdown, past the skin-friction maximum and to higher Reynolds numbers than investigated before to evaluate how these two flow regimes converge towards turbulence and what transitional flow structures embody the statistics and mean dynamics of developed turbulence. We show that H- and K-type breakdowns both relax toward the same statistical structure typical of developed turbulence at high Reynolds number immediately after the skin-friction maximum. This threshold marks the onset of self-sustaining mechanisms of near-wall turbulence. At this point, computed power spectra exhibit a decade of Kolmogorov inertial subrange; this is further evidence of convergence to equilibrium turbulence at the late stage of transition. Here, visualization of the instantaneous flow structure shows numerous, tightly packed hairpin vortices (Adrian, Phys. Fluids, vol. 19, 2007, 041301). Strongly organized coherent hairpin structures are less perceptible farther downstream (at higher Reynolds numbers), but the flow statistics and near-wall dynamics are the same. These structurally simple hairpin-packet solutions found in the very late stages of H- and K-type transitions obey the statistical measurements of higher-Reynolds-number turbulence. Comparison with the bypass transition of Wu & Moin (Phys. Fluids, vol. 22, 2010, pp. 85–105) extends these observations to a wider class of transitional flows. In contrast to bypass transition, the (time- and spanwise-averaged) skin-friction maximum in both H- and K-type transitions overshoots the turbulent correlation. Downstream of these friction maxima, all three skin-friction profiles collapse when plotted versus the momentum-thickness Reynolds number,
$\mathit{Ma}= 0. 2$), flat-plate boundary layers is studied by direct numerical simulation. We have validated the initial disturbance development, confirmed that H- and K-regime transitions were reproduced and, from these starting points, we carried these simulations beyond breakdown, past the skin-friction maximum and to higher Reynolds numbers than investigated before to evaluate how these two flow regimes converge towards turbulence and what transitional flow structures embody the statistics and mean dynamics of developed turbulence. We show that H- and K-type breakdowns both relax toward the same statistical structure typical of developed turbulence at high Reynolds number immediately after the skin-friction maximum. This threshold marks the onset of self-sustaining mechanisms of near-wall turbulence. At this point, computed power spectra exhibit a decade of Kolmogorov inertial subrange; this is further evidence of convergence to equilibrium turbulence at the late stage of transition. Here, visualization of the instantaneous flow structure shows numerous, tightly packed hairpin vortices (Adrian, Phys. Fluids, vol. 19, 2007, 041301). Strongly organized coherent hairpin structures are less perceptible farther downstream (at higher Reynolds numbers), but the flow statistics and near-wall dynamics are the same. These structurally simple hairpin-packet solutions found in the very late stages of H- and K-type transitions obey the statistical measurements of higher-Reynolds-number turbulence. Comparison with the bypass transition of Wu & Moin (Phys. Fluids, vol. 22, 2010, pp. 85–105) extends these observations to a wider class of transitional flows. In contrast to bypass transition, the (time- and spanwise-averaged) skin-friction maximum in both H- and K-type transitions overshoots the turbulent correlation. Downstream of these friction maxima, all three skin-friction profiles collapse when plotted versus the momentum-thickness Reynolds number, 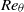 ${\mathit{Re}}_{\theta } $. Mean velocities, turbulence intensities and integral parameters collapse generally beyond
${\mathit{Re}}_{\theta } $. Mean velocities, turbulence intensities and integral parameters collapse generally beyond 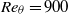 ${\mathit{Re}}_{\theta } = 900$ in each transition scenario. Skin-friction maxima, organized hairpin vortices and the onset of self-sustaining turbulence found in controlled H- and K-type transitions are, in many dynamically important respects, similar to development of turbulent spots seen by Park et al. (Phys. Fluids, vol. 24, 2012, 035105). A detailed statistical comparison demonstrates that each of these different transition scenarios evolve into a unique force balance characteristic of higher-Reynolds-number turbulence (Klewicki, Ebner & Wu, J. Fluid Mech., vol. 682, 2011, pp. 617–651). We postulate that these dynamics of late-stage transition as manifested by hairpin packets can serve as a reduced-order model of high-Reynolds-number turbulent boundary layers.
${\mathit{Re}}_{\theta } = 900$ in each transition scenario. Skin-friction maxima, organized hairpin vortices and the onset of self-sustaining turbulence found in controlled H- and K-type transitions are, in many dynamically important respects, similar to development of turbulent spots seen by Park et al. (Phys. Fluids, vol. 24, 2012, 035105). A detailed statistical comparison demonstrates that each of these different transition scenarios evolve into a unique force balance characteristic of higher-Reynolds-number turbulence (Klewicki, Ebner & Wu, J. Fluid Mech., vol. 682, 2011, pp. 617–651). We postulate that these dynamics of late-stage transition as manifested by hairpin packets can serve as a reduced-order model of high-Reynolds-number turbulent boundary layers.