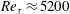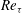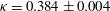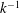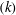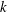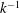1. Introduction
Recently, relatively ‘high’-Reynolds-number wall-bounded turbulence has been investigated with the help of innovations in measurement technologies (Nagib et al.
Reference Nagib, Christophorou, Reudi, Monkewitz, Österlun and Gravante2004; Kunkel & Marusic Reference Kunkel and Marusic2006; Westerweel, Elsinga & Adrian Reference Westerweel, Elsinga and Adrian2013; Bailey et al.
Reference Bailey, Vallikivi, Hultmark and Smits2014) and computation (Borrell, Sillero & Jiménez Reference Borrell, Sillero and Jiménez2013; El Khoury et al.
Reference El Khoury, Schlatter, Noorani, Fischer, Brethouwer and Johansson2013; Lee, Malaya & Moser Reference Lee, Malaya and Moser2013). Because of the simplicity in geometry and boundary conditions, pressure-driven turbulent flow between parallel walls (channel flow) is an excellent vehicle for the study of wall-bounded turbulence via direct numerical simulation (DNS). Since Kim, Moin & Moser (Reference Kim, Moin and Moser1987) showed agreement between DNS and experiments in channel flow in 1987, DNS of channel flow has been used to study wall-bounded turbulence at ever higher Reynolds numbers, as advances in computing power have allowed. For example, channel flow DNS has been performed at
![]() $\mathit{Re}_{{\it\tau}}=590$
(Moser, Kim & Mansour Reference Moser, Kim and Mansour1999),
$\mathit{Re}_{{\it\tau}}=590$
(Moser, Kim & Mansour Reference Moser, Kim and Mansour1999),
![]() $\mathit{Re}_{{\it\tau}}=950$
(Del Álamo et al.
Reference Del Álamo, Jiménez, Zandonade and Moser2004) and
$\mathit{Re}_{{\it\tau}}=950$
(Del Álamo et al.
Reference Del Álamo, Jiménez, Zandonade and Moser2004) and
![]() $\mathit{Re}_{{\it\tau}}=2000$
(Hoyas & Jiménez Reference Hoyas and Jiménez2006). More recently, simulations with
$\mathit{Re}_{{\it\tau}}=2000$
(Hoyas & Jiménez Reference Hoyas and Jiménez2006). More recently, simulations with
![]() $\mathit{Re}_{{\it\tau}}\approx 4000$
were performed separately by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) in a relatively small domain size and by Bernardini, Pirozzoli & Orlandi (Reference Bernardini, Pirozzoli and Orlandi2014). Moreover, to investigate the differences between channel flow turbulence and boundary layer turbulence, a simulation at
$\mathit{Re}_{{\it\tau}}\approx 4000$
were performed separately by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) in a relatively small domain size and by Bernardini, Pirozzoli & Orlandi (Reference Bernardini, Pirozzoli and Orlandi2014). Moreover, to investigate the differences between channel flow turbulence and boundary layer turbulence, a simulation at
![]() $\mathit{Re}_{{\it\tau}}=2000$
of a zero-pressure-gradient boundary layer was performed by Sillero, Jiménez & Moser (Reference Sillero, Jiménez and Moser2013).
$\mathit{Re}_{{\it\tau}}=2000$
of a zero-pressure-gradient boundary layer was performed by Sillero, Jiménez & Moser (Reference Sillero, Jiménez and Moser2013).
The idealized channel flow that is so straightforward to simulate is more difficult to realize experimentally because of the need for sidewalls. Measurements of channel flow are not as numerous as for other wall-bounded turbulent flows, but a number of studies have been conducted over the years (Comte-Bellot Reference Comte-Bellot1963; Dean & Bradshaw Reference Dean and Bradshaw1976; Johansson & Alfredsson Reference Johansson and Alfredsson1982; Wei & Willmarth Reference Wei and Willmarth1989; Zanoun, Durst & Nagib Reference Zanoun, Durst and Nagib2003; Monty & Chong Reference Monty and Chong2009; Zanoun, Nagib & Durst Reference Zanoun, Nagib and Durst2009). Of particular interest here will be the channel measurements made by Schultz & Flack (Reference Schultz and Flack2013) at Reynolds number up to
![]() $\mathit{Re}_{{\it\tau}}=6000$
, because they bracket the Reynolds number simulated here.
$\mathit{Re}_{{\it\tau}}=6000$
, because they bracket the Reynolds number simulated here.
Turbulent flows with
![]() $\mathit{Re}_{{\it\tau}}$
of the order of
$\mathit{Re}_{{\it\tau}}$
of the order of
![]() $10^{3}$
and greater are of interest because this is the range of Reynolds numbers relevant to industrial applications (Smits & Marusic Reference Smits and Marusic2013). Further, it is in this range that characteristics of wall-bounded turbulence associated with high Reynolds number are first manifested (Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
), and so studies of these phenomena must necessarily be conducted at these Reynolds numbers. The best-known feature of high-Reynolds-number wall-bounded turbulence is the logarithmic law in the mean velocity, which has been known since the 1930s (Millikan Reference Millikan1938). The von Kármán constant
$10^{3}$
and greater are of interest because this is the range of Reynolds numbers relevant to industrial applications (Smits & Marusic Reference Smits and Marusic2013). Further, it is in this range that characteristics of wall-bounded turbulence associated with high Reynolds number are first manifested (Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
), and so studies of these phenomena must necessarily be conducted at these Reynolds numbers. The best-known feature of high-Reynolds-number wall-bounded turbulence is the logarithmic law in the mean velocity, which has been known since the 1930s (Millikan Reference Millikan1938). The von Kármán constant
![]() ${\it\kappa}$
that appears in the log law is also an important parameter for calibrating turbulence models (Spalart & Allmaras Reference Spalart and Allmaras1992; Durbin & Pettersson Reif Reference Durbin and Pettersson Reif2010; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011). It was considered universal in the past, but Nagib & Chauhan (Reference Nagib and Chauhan2008) showed that
${\it\kappa}$
that appears in the log law is also an important parameter for calibrating turbulence models (Spalart & Allmaras Reference Spalart and Allmaras1992; Durbin & Pettersson Reif Reference Durbin and Pettersson Reif2010; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011). It was considered universal in the past, but Nagib & Chauhan (Reference Nagib and Chauhan2008) showed that
![]() ${\it\kappa}$
can be different in different flow geometries. Further, Jiménez & Moser (Reference Jiménez and Moser2007) found that channel flows with
${\it\kappa}$
can be different in different flow geometries. Further, Jiménez & Moser (Reference Jiménez and Moser2007) found that channel flows with
![]() $\mathit{Re}_{{\it\tau}}$
up to 2000 do not exhibit a region where the mean velocity profile strictly follows a logarithmic law, and showed that a finite-Reynolds-number correction like that introduced by Afzal (Reference Afzal1976) was more consistent with data in this Reynolds number range. Similarly, Mizuno & Jiménez (Reference Mizuno and Jiménez2011) used a different finite-Reynolds-number correction to represent the overlap region in boundary layers, channels and pipes.
$\mathit{Re}_{{\it\tau}}$
up to 2000 do not exhibit a region where the mean velocity profile strictly follows a logarithmic law, and showed that a finite-Reynolds-number correction like that introduced by Afzal (Reference Afzal1976) was more consistent with data in this Reynolds number range. Similarly, Mizuno & Jiménez (Reference Mizuno and Jiménez2011) used a different finite-Reynolds-number correction to represent the overlap region in boundary layers, channels and pipes.
For turbulent intensities, Townsend (Reference Townsend1976) predicted that, in high-Reynolds-number flows, there are regions where the variance of the streamwise and spanwise velocity components decreases logarithmically with distance from the wall. This has been observed experimentally for streamwise (Kunkel & Marusic Reference Kunkel and Marusic2006; Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012; Hutchins et al.
Reference Hutchins, Chauhan, Marusic, Monty and Klewicki2012; Winkel et al.
Reference Winkel, Cutbirth, Ceccio, Perlin and Dowling2012; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013) and spanwise components (Fernholz & Finley Reference Fernholz and Finley1996; Morrison et al.
Reference Morrison, McKeon, Jiang and Smits2004), but has only been observed in the spanwise component in DNS (Hoyas & Jiménez Reference Hoyas and Jiménez2008; Sillero et al.
Reference Sillero, Jiménez and Moser2013). Further, the peak of the streamwise velocity variance has a weak Reynolds number dependence when it is scaled by the friction velocity,
![]() $u_{{\it\tau}}$
(DeGraaff & Eaton Reference DeGraaff and Eaton2000; Hoyas & Jiménez Reference Hoyas and Jiménez2006).
$u_{{\it\tau}}$
(DeGraaff & Eaton Reference DeGraaff and Eaton2000; Hoyas & Jiménez Reference Hoyas and Jiménez2006).
There has also been recent interest in the role of large-scale motions (LSMs) in high-Reynolds-number wall-bounded turbulent flow (Kim & Adrian Reference Kim and Adrian1999; Hutchins & Marusic Reference Hutchins and Marusic2007; Wu, Baltzer & Adrian Reference Wu, Baltzer and Adrian2012). According to the scaling analysis of Perry, Henbest & Chong (Reference Perry, Henbest and Chong1986) there is a region where the one-dimensional spectral energy density has a
![]() $k_{x}^{-1}$
dependence (
$k_{x}^{-1}$
dependence (
![]() $k_{x}$
, wavenumber in streamwise direction). This has been supported by experimental evidence (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005, Reference Nickels, Marusic, Hafez, Hutchins and Chong2007; Dixit & Ramesh Reference Dixit and Ramesh2013), but not numerical simulations.
$k_{x}$
, wavenumber in streamwise direction). This has been supported by experimental evidence (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005, Reference Nickels, Marusic, Hafez, Hutchins and Chong2007; Dixit & Ramesh Reference Dixit and Ramesh2013), but not numerical simulations.
In summary, there are many characteristics of high-Reynolds-number wall-bounded turbulence that have been suggested by theoretical arguments and corroborated experimentally, but which have not been observed in direct numerical simulations, presumably due to the limited Reynolds numbers of the simulations. This is unfortunate because such simulations could provide detailed information about these high-Reynolds-number phenomena that would not otherwise be available. The DNS reported here was undertaken to address this issue, by simulating a channel flow at sufficiently high Reynolds number and with a sufficiently large spatial domain to exhibit characteristics of high-Reynolds-number turbulence like those discussed above. The simulation was performed for
![]() $\mathit{Re}_{{\it\tau}}\approx 5200$
with the same domain size as used by Hoyas & Jiménez (Reference Hoyas and Jiménez2006) in their
$\mathit{Re}_{{\it\tau}}\approx 5200$
with the same domain size as used by Hoyas & Jiménez (Reference Hoyas and Jiménez2006) in their
![]() $\mathit{Re}_{{\it\tau}}=2000$
simulation.
$\mathit{Re}_{{\it\tau}}=2000$
simulation.
This paper is organized as follows. First, the simulation methods and parameters are described in § 2, along with other simulations and experiments used for comparison. Results of the simulation that arise due to the relatively high Reynolds number of the simulation are presented in § 3. Finally, conclusions are offered in § 4.
2. Simulation details
In the discussion to follow, the streamwise, wall-normal and spanwise velocities will be denoted
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
respectively, with the mean velocity indicated by a capital letter and fluctuations by a prime. Furthermore,
$w$
respectively, with the mean velocity indicated by a capital letter and fluctuations by a prime. Furthermore,
![]() $\langle \cdot \rangle$
indicates the expected value or average. Thus,
$\langle \cdot \rangle$
indicates the expected value or average. Thus,
![]() $U=\langle u\rangle$
and
$U=\langle u\rangle$
and
![]() $u=U+u^{\prime }$
.
$u=U+u^{\prime }$
.
The simulations reported here are DNS of incompressible turbulent flow between two parallel planes. Periodic boundary conditions are applied in the streamwise (
![]() $x$
) and spanwise (
$x$
) and spanwise (
![]() $z$
) directions, and no-slip/no-penetration boundary conditions are applied at the wall. The computational domain sizes are
$z$
) directions, and no-slip/no-penetration boundary conditions are applied at the wall. The computational domain sizes are
![]() $L_{x}=8{\rm\pi}{\it\delta}$
and
$L_{x}=8{\rm\pi}{\it\delta}$
and
![]() $L_{z}=3{\rm\pi}{\it\delta}$
, where
$L_{z}=3{\rm\pi}{\it\delta}$
, where
![]() ${\it\delta}$
is the channel half-width, so the domain size in the wall-normal (
${\it\delta}$
is the channel half-width, so the domain size in the wall-normal (
![]() $y$
) direction is
$y$
) direction is
![]() $2{\it\delta}$
. The flow is driven by a uniform pressure gradient, which varies in time to ensure that the mass flux through the channel remains constant.
$2{\it\delta}$
. The flow is driven by a uniform pressure gradient, which varies in time to ensure that the mass flux through the channel remains constant.
A Fourier–Galerkin method is used in the streamwise and spanwise directions, while the wall-normal direction is represented using a B-spline collocation method (Kwok, Moser & Jiménez Reference Kwok, Moser and Jiménez2001; Botella & Shariff Reference Botella and Shariff2003). The Navier–Stokes equations are solved using the method of Kim et al. (Reference Kim, Moin and Moser1987), in which equations for the wall-normal vorticity and the Laplacian of the wall-normal velocity are time-advanced. This formulation has the advantage of satisfying the continuity constraint exactly while eliminating the pressure. A low-storage implicit–explicit scheme (Spalart, Moser & Rogers Reference Spalart, Moser and Rogers1991) based on third-order Runge–Kutta for the nonlinear terms and Crank–Nicolson for the viscous terms is used to advance in time. The time step is adjusted to maintain an approximately constant Courant–Friedrichs–Lewy (CFL) number of one. A new highly optimized code was developed to solve the Navier–Stokes equations using these methods on advanced petascale computer architectures. For more details about the code, the numerical methods and how the simulations were run see Lee et al. (Reference Lee, Malaya and Moser2013, Reference Lee, Ulerich, Malaya and Moser2014).
The simulations performed here were conducted with resolution comparable to that used in previous high-Reynolds-number channel flow simulations, when measured in wall units. Normalization in wall units, that is with kinematic viscosity
![]() ${\it\nu}$
and friction velocity
${\it\nu}$
and friction velocity
![]() $u_{{\it\tau}}$
, is indicated with a superscript ‘
$u_{{\it\tau}}$
, is indicated with a superscript ‘
![]() $+$
’. The friction velocity is
$+$
’. The friction velocity is
![]() $u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, where
$u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, where
![]() ${\it\tau}_{w}$
is the mean wall shear stress and
${\it\tau}_{w}$
is the mean wall shear stress and
![]() ${\it\rho}$
is density. For the highest-Reynolds-number simulation reported here, which is designated LM5200,
${\it\rho}$
is density. For the highest-Reynolds-number simulation reported here, which is designated LM5200,
![]() $N_{x}=10\,240$
and
$N_{x}=10\,240$
and
![]() $N_{z}=7680$
Fourier modes were used to represent the streamwise and spanwise directions, which results in an effective resolution of
$N_{z}=7680$
Fourier modes were used to represent the streamwise and spanwise directions, which results in an effective resolution of
![]() ${\rm\Delta}x^{+}=L_{x}^{+}/N_{x}=12.7$
and
${\rm\Delta}x^{+}=L_{x}^{+}/N_{x}=12.7$
and
![]() ${\rm\Delta}z^{+}=L_{z}^{+}/N_{z}=6.4$
. In the wall-normal direction, the seventh-order B-splines are defined on a set of
${\rm\Delta}z^{+}=L_{z}^{+}/N_{z}=6.4$
. In the wall-normal direction, the seventh-order B-splines are defined on a set of
![]() $1530=N_{y}-6$
knot points (
$1530=N_{y}-6$
knot points (
![]() $N_{y}$
is the number of B-spline basis functions), which are distributed uniformly in a mapped coordinate
$N_{y}$
is the number of B-spline basis functions), which are distributed uniformly in a mapped coordinate
![]() ${\it\xi}$
that is related to the wall-normal coordinate
${\it\xi}$
that is related to the wall-normal coordinate
![]() $y$
through
$y$
through
The single parameter
![]() ${\it\eta}$
in this mapping controls how strongly the knot points are clustered near the wall, with the strongest clustering occurring when
${\it\eta}$
in this mapping controls how strongly the knot points are clustered near the wall, with the strongest clustering occurring when
![]() ${\it\eta}=1$
. In LM5200,
${\it\eta}=1$
. In LM5200,
![]() ${\it\eta}=0.97$
, resulting in the first knot point from the wall at
${\it\eta}=0.97$
, resulting in the first knot point from the wall at
![]() ${\rm\Delta}y_{w}^{+}=0.498$
and the centreline knot spacing of
${\rm\Delta}y_{w}^{+}=0.498$
and the centreline knot spacing of
![]() ${\rm\Delta}y_{c}^{+}=10.3$
. The
${\rm\Delta}y_{c}^{+}=10.3$
. The
![]() $N_{y}$
collocation points are determined as the Greville abscissae (Johnson Reference Johnson2005), in which, for
$N_{y}$
collocation points are determined as the Greville abscissae (Johnson Reference Johnson2005), in which, for
![]() $n$
-degree splines, each collocation point is the average of
$n$
-degree splines, each collocation point is the average of
![]() $n$
consecutive knot points (
$n$
consecutive knot points (
![]() $n=7$
here), with the knots at the boundary given a multiplicity of
$n=7$
here), with the knots at the boundary given a multiplicity of
![]() $n-1$
. As a result, the collocation points are more clustered near the wall than the knot points. Resolution parameters for all the simulations discussed here are provided in table 1.
$n-1$
. As a result, the collocation points are more clustered near the wall than the knot points. Resolution parameters for all the simulations discussed here are provided in table 1.
Table 1. Summary of simulation parameters. Here,
![]() ${\rm\Delta}x$
and
${\rm\Delta}x$
and
![]() ${\rm\Delta}z$
are in terms of Fourier modes for spectral methods,
${\rm\Delta}z$
are in terms of Fourier modes for spectral methods,
![]() ${\rm\Delta}y_{w}$
and
${\rm\Delta}y_{w}$
and
![]() ${\rm\Delta}y_{c}$
represent the grid spacing at the wall and the centreline respectively,
${\rm\Delta}y_{c}$
represent the grid spacing at the wall and the centreline respectively,
![]() ${\it\delta}$
is the channel half-width,
${\it\delta}$
is the channel half-width,
![]() $\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu}$
,
$\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu}$
,
![]() $Tu_{{\it\tau}}/{\it\delta}$
is the total simulation time without transition; SB denotes spectral/B-spline, SC denotes spectral/compact finite difference, FD denotes finite difference and LDV denotes laser doppler velocimetry.
$Tu_{{\it\tau}}/{\it\delta}$
is the total simulation time without transition; SB denotes spectral/B-spline, SC denotes spectral/compact finite difference, FD denotes finite difference and LDV denotes laser doppler velocimetry.

Because the mass flux in the channel remains constant, the bulk Reynolds number
![]() $\mathit{Re}_{b}$
can be specified directly for a simulation, where
$\mathit{Re}_{b}$
can be specified directly for a simulation, where
![]() $\mathit{Re}_{b}=U_{b}{\it\delta}/{\it\nu}$
,
$\mathit{Re}_{b}=U_{b}{\it\delta}/{\it\nu}$
,
![]() $U_{b}=(1/2{\it\delta})\int _{-{\it\delta}}^{{\it\delta}}U(y)\,\text{d}y$
and
$U_{b}=(1/2{\it\delta})\int _{-{\it\delta}}^{{\it\delta}}U(y)\,\text{d}y$
and
![]() $U(y)$
is the mean streamwise velocity. Four simulations at four different Reynolds numbers were conducted. Of most interest here is the highest-Reynolds-number case, LM5200, for which the bulk Reynolds number is
$U(y)$
is the mean streamwise velocity. Four simulations at four different Reynolds numbers were conducted. Of most interest here is the highest-Reynolds-number case, LM5200, for which the bulk Reynolds number is
![]() $\mathit{Re}_{b}=1.25\times 10^{5}$
and the friction Reynolds number is
$\mathit{Re}_{b}=1.25\times 10^{5}$
and the friction Reynolds number is
![]() $\mathit{Re}_{{\it\tau}}=5186~(\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu})$
. The three other cases simulated, LM180, LM550 and LM1000, were performed for convenience to regenerate data for previously simulated cases (Kim et al.
Reference Kim, Moin and Moser1987; Moser et al.
Reference Moser, Kim and Mansour1999; Del Álamo et al.
Reference Del Álamo, Jiménez, Zandonade and Moser2004) using the numerical methods used here. The simulation details for each case are summarized in table 1.
$\mathit{Re}_{{\it\tau}}=5186~(\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu})$
. The three other cases simulated, LM180, LM550 and LM1000, were performed for convenience to regenerate data for previously simulated cases (Kim et al.
Reference Kim, Moin and Moser1987; Moser et al.
Reference Moser, Kim and Mansour1999; Del Álamo et al.
Reference Del Álamo, Jiménez, Zandonade and Moser2004) using the numerical methods used here. The simulation details for each case are summarized in table 1.
In addition, channel flow data from four other sources in the literature are included here for comparison. The first is a simulation at
![]() $\mathit{Re}_{{\it\tau}}=2000$
conducted by Hoyas & Jiménez (Reference Hoyas and Jiménez2006, HJ2000), which used the same domain size and a similar numerical scheme to the current simulations, differing only in the use of high-order compact finite differences in the wall-normal direction, rather than B-splines. A second simulation (LJ4200) by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) was at
$\mathit{Re}_{{\it\tau}}=2000$
conducted by Hoyas & Jiménez (Reference Hoyas and Jiménez2006, HJ2000), which used the same domain size and a similar numerical scheme to the current simulations, differing only in the use of high-order compact finite differences in the wall-normal direction, rather than B-splines. A second simulation (LJ4200) by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) was at
![]() $\mathit{Re}_{{\it\tau}}=4179$
and used the same numerical methods as HJ2000, but the domain size in
$\mathit{Re}_{{\it\tau}}=4179$
and used the same numerical methods as HJ2000, but the domain size in
![]() $x$
and
$x$
and
![]() $z$
was much smaller. The third simulation (BP04100), which was performed by Bernardini et al. (Reference Bernardini, Pirozzoli and Orlandi2014), was at
$z$
was much smaller. The third simulation (BP04100), which was performed by Bernardini et al. (Reference Bernardini, Pirozzoli and Orlandi2014), was at
![]() $\mathit{Re}_{{\it\tau}}=4079$
and used a domain size not much smaller than that used here, but these simulations were performed using second-order finite differences. Finally, experimental data from laser Doppler velocimetry measurements at two Reynolds numbers (
$\mathit{Re}_{{\it\tau}}=4079$
and used a domain size not much smaller than that used here, but these simulations were performed using second-order finite differences. Finally, experimental data from laser Doppler velocimetry measurements at two Reynolds numbers (
![]() $\mathit{Re}_{{\it\tau}}=4048$
and 5895, SF4000 and SF6000 respectively) are reported by Schultz & Flack (Reference Schultz and Flack2013) and are also included here for comparison. Summaries of all these data sources are also included in table 1.
$\mathit{Re}_{{\it\tau}}=4048$
and 5895, SF4000 and SF6000 respectively) are reported by Schultz & Flack (Reference Schultz and Flack2013) and are also included here for comparison. Summaries of all these data sources are also included in table 1.
We used the method described by Oliver et al. (Reference Oliver, Malaya, Ulerich and Moser2014) to estimate the uncertainty in the statistics reported here due to sampling noise. For LM5200, the estimated standard deviation of the mean velocity is less than 0.2 % and the estimated standard deviation of the variance and covariance of the velocity components is less than 0.5 % in the near-wall region (
![]() $y^{+}<100$
say) and 3 % in the outer region (
$y^{+}<100$
say) and 3 % in the outer region (
![]() $y>0.2{\it\delta}$
say). We also used the total stress and the Reynolds stress transport equations to test whether the simulated turbulence was statistically stationary. In a statistically stationary turbulent channel, the total stress, which is the sum of Reynolds stress and mean viscous stress, is linear due to momentum conservation:
$y>0.2{\it\delta}$
say). We also used the total stress and the Reynolds stress transport equations to test whether the simulated turbulence was statistically stationary. In a statistically stationary turbulent channel, the total stress, which is the sum of Reynolds stress and mean viscous stress, is linear due to momentum conservation:
As shown in figure 1(a), the discrepancy between the analytic linear profile and total stress profile from the simulations is less than 0.002 (in plus units) in all simulations, and it is much smaller than the standard deviation of the estimated total stress of LM5200.

Figure 1. Statistical stationarity of simulation. (a) The residual in (2.2), with the linestyle legend given in table 1; the dotted line is the standard deviation of the estimated total stress in LM5200. (b) The residual in (2.3) of LM5200 (solid), and the standard deviation of the estimated statistical error in the sum of the right-hand side terms in (2.3) (dashed).
The Reynolds stress transport equations, which govern the evolution of the Reynolds stress tensor, are given by
 $$\begin{eqnarray}\displaystyle \frac{\text{D}\langle u_{i}^{\prime }u_{j}^{\prime }\rangle }{\text{D}t} & = & \displaystyle -\left(\langle u_{i}^{\prime }u_{k}^{\prime }\rangle \frac{\partial U_{j}}{\partial x_{k}}+\langle u_{j}^{\prime }u_{k}^{\prime }\rangle \frac{\partial U_{i}}{\partial x_{k}}\right)-\frac{\partial \langle u_{i}^{\prime }u_{j}^{\prime }u_{k}^{\prime }\rangle }{\partial x_{k}}+{\it\nu}\frac{\partial ^{2}\langle u_{i}^{\prime }u_{j}^{\prime }\rangle }{\partial x_{k}\partial x_{k}}\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle p^{\prime }\left(\frac{\partial u_{i}^{\prime }}{\partial x_{j}}+\frac{\partial u_{j}^{\prime }}{\partial x_{i}}\right)\right\rangle -\left(\frac{\partial \langle p^{\prime }u_{i}^{\prime }\rangle }{\partial x_{j}}+\frac{\partial \langle p^{\prime }u_{j}^{\prime }\rangle }{\partial x_{i}}\right)-2{\it\nu}\left\langle \frac{\partial u_{i}^{\prime }}{\partial x_{k}}\frac{\partial u_{j}^{\prime }}{\partial x_{k}}\right\rangle .\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{D}\langle u_{i}^{\prime }u_{j}^{\prime }\rangle }{\text{D}t} & = & \displaystyle -\left(\langle u_{i}^{\prime }u_{k}^{\prime }\rangle \frac{\partial U_{j}}{\partial x_{k}}+\langle u_{j}^{\prime }u_{k}^{\prime }\rangle \frac{\partial U_{i}}{\partial x_{k}}\right)-\frac{\partial \langle u_{i}^{\prime }u_{j}^{\prime }u_{k}^{\prime }\rangle }{\partial x_{k}}+{\it\nu}\frac{\partial ^{2}\langle u_{i}^{\prime }u_{j}^{\prime }\rangle }{\partial x_{k}\partial x_{k}}\nonumber\\ \displaystyle & & \displaystyle +\,\left\langle p^{\prime }\left(\frac{\partial u_{i}^{\prime }}{\partial x_{j}}+\frac{\partial u_{j}^{\prime }}{\partial x_{i}}\right)\right\rangle -\left(\frac{\partial \langle p^{\prime }u_{i}^{\prime }\rangle }{\partial x_{j}}+\frac{\partial \langle p^{\prime }u_{j}^{\prime }\rangle }{\partial x_{i}}\right)-2{\it\nu}\left\langle \frac{\partial u_{i}^{\prime }}{\partial x_{k}}\frac{\partial u_{j}^{\prime }}{\partial x_{k}}\right\rangle .\quad\end{eqnarray}$$
While not reported here, all the terms on the right-hand side of (2.3) have been computed from our simulations, and the data are available at http://turbulence.ices.utexas.edu. In a statistically stationary channel flow, the substantial derivative on the left-hand side of (2.3) is zero. Hence, any deviation from zero of the sum of the terms on the right-hand side of (2.3) is an indicator that the flow is not stationary. The residual of (2.3) is shown in figure 1(b) (solid lines) in wall units. The values for all components of the Reynolds stress are much less than 0.0001 in wall units, which is less than 0.01 % error in the balance near the wall. The relative error in the balance increases to of the order of 1 % away from the wall, as the magnitude of the terms in (2.3) decreases. Across the entire channel, the estimated standard deviation of the statistical noise (dashed lines) is much larger than these discrepancies.
3. Results
3.1. Mean velocity profile
The multiscale character of wall-bounded turbulence, in which
![]() ${\it\nu}/u_{{\it\tau}}$
is the length scale relevant to the near-wall flow and
${\it\nu}/u_{{\it\tau}}$
is the length scale relevant to the near-wall flow and
![]() ${\it\delta}$
applies to the flow away from the wall, is well known. As first noted by Millikan (Reference Millikan1938), this scaling behaviour and asymptotic matching lead to the logarithmic variation of mean streamwise velocity with the distance from the wall in an overlap region between the inner and outer flows. This ‘log law’ is given by
${\it\delta}$
applies to the flow away from the wall, is well known. As first noted by Millikan (Reference Millikan1938), this scaling behaviour and asymptotic matching lead to the logarithmic variation of mean streamwise velocity with the distance from the wall in an overlap region between the inner and outer flows. This ‘log law’ is given by
where
![]() ${\it\kappa}$
is the von Kármán constant. In a log layer, the indicator function
${\it\kappa}$
is the von Kármán constant. In a log layer, the indicator function
is constant and equal to
![]() $1/{\it\kappa}$
. Hence, the indicator function,
$1/{\it\kappa}$
. Hence, the indicator function,
![]() ${\it\beta}$
, will have a plateau if there is a logarithmic layer.
${\it\beta}$
, will have a plateau if there is a logarithmic layer.
The mean streamwise velocity profile is shown in figure 2 for all the data sets listed in table 1. The profiles from all the relatively high-Reynolds-number cases are consistent, as expected. Despite this agreement, the indicator function
![]() ${\it\beta}$
shows some disagreement between the three highest-Reynolds-number simulations, as shown in figure 3(a). In the LM5200 case,
${\it\beta}$
shows some disagreement between the three highest-Reynolds-number simulations, as shown in figure 3(a). In the LM5200 case,
![]() ${\it\beta}$
is approximately flat between
${\it\beta}$
is approximately flat between
![]() $y^{+}=350$
and
$y^{+}=350$
and
![]() $y/{\it\delta}=0.16~(y^{+}=830)$
, indicating a log layer in this region. The LJ4200 case also appears to be converging towards a plateau in this region, but there is apparent statistical noise in the profile, which is understandable given the small domain size. However, the BPO4100 simulation does not have a plateau in
$y/{\it\delta}=0.16~(y^{+}=830)$
, indicating a log layer in this region. The LJ4200 case also appears to be converging towards a plateau in this region, but there is apparent statistical noise in the profile, which is understandable given the small domain size. However, the BPO4100 simulation does not have a plateau in
![]() ${\it\beta}$
. There is also a small discrepancy between BPO4100 and the other two cases from
${\it\beta}$
. There is also a small discrepancy between BPO4100 and the other two cases from
![]() $y^{+}\approx 30$
to 100. These discrepancies are significantly larger than the statistical uncertainty in the value of
$y^{+}\approx 30$
to 100. These discrepancies are significantly larger than the statistical uncertainty in the value of
![]() ${\it\beta}$
(approximately 0.2 %) in the current simulations, and presumably in the BPO4100 simulations, as the averaging time and domain sizes are comparable.
${\it\beta}$
(approximately 0.2 %) in the current simulations, and presumably in the BPO4100 simulations, as the averaging time and domain sizes are comparable.

Figure 2. Mean streamwise velocity profile for all the cases listed in table 1, where the legend of line styles and symbols is also given.

Figure 3. Log-law indicator function
![]() ${\it\beta}$
for (a) the highest-Reynolds-number simulations, LM5200, LJ4200 and BPO4100, (b) simulations at
${\it\beta}$
for (a) the highest-Reynolds-number simulations, LM5200, LJ4200 and BPO4100, (b) simulations at
![]() $\mathit{Re}_{{\it\tau}}=5186$
, 2003 and 1000 (LM5200, HJ2000 and LM1000), and (c) simulation LM5200 along with the expressions ((3.3), star) and ((3.4), diamond). In (a), the horizontal dashed line is at
$\mathit{Re}_{{\it\tau}}=5186$
, 2003 and 1000 (LM5200, HJ2000 and LM1000), and (c) simulation LM5200 along with the expressions ((3.3), star) and ((3.4), diamond). In (a), the horizontal dashed line is at
![]() ${\it\beta}=1/{\it\kappa}=1/0.384$
, and in (c) parameter values (see table 2) fitted from LM5200 are solid, and those from Jiménez & Moser (Reference Jiménez and Moser2007), Mizuno & Jiménez (Reference Mizuno and Jiménez2011) are dashed. The linestyle legend for (a) and (b) is given in table 1.
${\it\beta}=1/{\it\kappa}=1/0.384$
, and in (c) parameter values (see table 2) fitted from LM5200 are solid, and those from Jiménez & Moser (Reference Jiménez and Moser2007), Mizuno & Jiménez (Reference Mizuno and Jiménez2011) are dashed. The linestyle legend for (a) and (b) is given in table 1.
The values of
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $B$
in (3.1) were determined by fitting the mean velocity data from LM5200 in the region between
$B$
in (3.1) were determined by fitting the mean velocity data from LM5200 in the region between
![]() $y^{+}=350$
and
$y^{+}=350$
and
![]() $y/{\it\delta}=0.16$
to obtain the values of
$y/{\it\delta}=0.16$
to obtain the values of
![]() $0.384\pm 0.004$
and 4.27 respectively, with
$0.384\pm 0.004$
and 4.27 respectively, with
![]() $R^{2}=0.9999$
, where
$R^{2}=0.9999$
, where
![]() $R^{2}$
is the coefficient of determination, which is one for a perfect fit. The value of
$R^{2}$
is the coefficient of determination, which is one for a perfect fit. The value of
![]() ${\it\kappa}$
agrees with the value computed by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014), but shows a slight discrepancy with the values measured by Monty (Reference Monty2005) and Nagib & Chauhan (Reference Nagib and Chauhan2008), which are
${\it\kappa}$
agrees with the value computed by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014), but shows a slight discrepancy with the values measured by Monty (Reference Monty2005) and Nagib & Chauhan (Reference Nagib and Chauhan2008), which are
![]() ${\it\kappa}=0.37$
and 0.39 respectively. The value of
${\it\kappa}=0.37$
and 0.39 respectively. The value of
![]() ${\it\kappa}$
obtained here is remarkably similar to those reported by Österlund et al. (Reference Österlund, Johansson, Nagib and Hites2000),
${\it\kappa}$
obtained here is remarkably similar to those reported by Österlund et al. (Reference Österlund, Johansson, Nagib and Hites2000),
![]() ${\it\kappa}=0.38$
, and Nagib & Chauhan (Reference Nagib and Chauhan2008),
${\it\kappa}=0.38$
, and Nagib & Chauhan (Reference Nagib and Chauhan2008),
![]() ${\it\kappa}=0.384$
, in the zero-pressure-gradient boundary layer. However, the value of
${\it\kappa}=0.384$
, in the zero-pressure-gradient boundary layer. However, the value of
![]() ${\it\kappa}$
reported here is smaller than
${\it\kappa}$
reported here is smaller than
![]() ${\it\kappa}=0.40$
measured by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014) in pipe flow. It should be noted that the choice of the range for this curve fit is somewhat arbitrary, since the indicator function is not exactly flat (figure 3
c).
${\it\kappa}=0.40$
measured by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014) in pipe flow. It should be noted that the choice of the range for this curve fit is somewhat arbitrary, since the indicator function is not exactly flat (figure 3
c).
From an asymptotic analysis perspective, the log-law relation (3.1) is the lowest-order truncation of a matched asymptotic expansion in
![]() $1/\mathit{Re}_{{\it\tau}}$
(Afzal & Yajnik Reference Afzal and Yajnik1973; Jiménez & Moser Reference Jiménez and Moser2007). Several higher-order representations of the mean velocity in the overlap region have been evaluated based on experimental and DNS data in boundary layers, channels and pipes (Buschmann & Gad-el-Hak Reference Buschmann and Gad-el-Hak2003; Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011). Here, we consider two such applications to channels in the context of the LM5200 data.
$1/\mathit{Re}_{{\it\tau}}$
(Afzal & Yajnik Reference Afzal and Yajnik1973; Jiménez & Moser Reference Jiménez and Moser2007). Several higher-order representations of the mean velocity in the overlap region have been evaluated based on experimental and DNS data in boundary layers, channels and pipes (Buschmann & Gad-el-Hak Reference Buschmann and Gad-el-Hak2003; Jiménez & Moser Reference Jiménez and Moser2007; Mizuno & Jiménez Reference Mizuno and Jiménez2011). Here, we consider two such applications to channels in the context of the LM5200 data.
Jiménez & Moser (Reference Jiménez and Moser2007) considered a higher-order truncation in which
![]() ${\it\beta}$
has the form
${\it\beta}$
has the form
This formulation essentially allows for an
![]() $\mathit{Re}_{{\it\tau}}$
dependence of
$\mathit{Re}_{{\it\tau}}$
dependence of
![]() ${\it\kappa}=(1/{\it\kappa}_{\infty }+{\it\alpha}_{1}/\mathit{Re}_{{\it\tau}})^{-1}$
, and introduces a linear dependence on
${\it\kappa}=(1/{\it\kappa}_{\infty }+{\it\alpha}_{1}/\mathit{Re}_{{\it\tau}})^{-1}$
, and introduces a linear dependence on
![]() $y/{\it\delta}=y^{+}/\mathit{Re}_{{\it\tau}}$
. Based on data from a simulation at
$y/{\it\delta}=y^{+}/\mathit{Re}_{{\it\tau}}$
. Based on data from a simulation at
![]() $\mathit{Re}_{{\it\tau}}\approx 1000$
by Del Álamo et al. (Reference Del Álamo, Jiménez, Zandonade and Moser2004, similar to LM1000) and from HJ2000 (see figure 3
b), they determined the parameter values shown in table 2. Further, this form and these values were found to be consistent with experimental measurements by Christensen & Adrian (Reference Christensen and Adrian2001) at Reynolds numbers up to
$\mathit{Re}_{{\it\tau}}\approx 1000$
by Del Álamo et al. (Reference Del Álamo, Jiménez, Zandonade and Moser2004, similar to LM1000) and from HJ2000 (see figure 3
b), they determined the parameter values shown in table 2. Further, this form and these values were found to be consistent with experimental measurements by Christensen & Adrian (Reference Christensen and Adrian2001) at Reynolds numbers up to
![]() $\mathit{Re}_{{\it\tau}}=2433$
.
$\mathit{Re}_{{\it\tau}}=2433$
.
Table 2. Values of parameters in (3.3) and (3.4) appropriate for
![]() $\mathit{Re}_{{\it\tau}}=5186$
as determined by Jiménez & Moser (Reference Jiménez and Moser2007) and Mizuno & Jiménez (Reference Mizuno and Jiménez2011) and from the LM5200 data.
$\mathit{Re}_{{\it\tau}}=5186$
as determined by Jiménez & Moser (Reference Jiménez and Moser2007) and Mizuno & Jiménez (Reference Mizuno and Jiménez2011) and from the LM5200 data.

Mizuno & Jiménez (Reference Mizuno and Jiménez2011) considered a different higher-order asymptotic truncation, for which
![]() ${\it\beta}$
is given by
${\it\beta}$
is given by
The second term was motivated by the form of a wake model that is quadratic for small
![]() $y/{\it\delta}$
, where the coefficient is related to the wake parameter
$y/{\it\delta}$
, where the coefficient is related to the wake parameter
![]() ${\it\Pi}$
by
${\it\Pi}$
by
![]() $a_{2}=(12{\it\Pi}-2)/{\it\kappa}$
. The term
$a_{2}=(12{\it\Pi}-2)/{\it\kappa}$
. The term
![]() $a_{1}$
is an offset (virtual origin) which accounts for the presence of the viscous layer (Wosnik, Castillo & George Reference Wosnik, Castillo and George2000). To first order in
$a_{1}$
is an offset (virtual origin) which accounts for the presence of the viscous layer (Wosnik, Castillo & George Reference Wosnik, Castillo and George2000). To first order in
![]() $a_{1}/y^{+}$
, the offset is equivalent to including an additive
$a_{1}/y^{+}$
, the offset is equivalent to including an additive
![]() $a_{1}/{\it\kappa}y^{+}$
term, which is expected from the matched asymptotics. They fitted the inverse of the mean velocity derivative to
$a_{1}/{\it\kappa}y^{+}$
term, which is expected from the matched asymptotics. They fitted the inverse of the mean velocity derivative to
![]() $y^{+}/{\it\beta}$
from (3.4) using the experimental and DNS data mentioned above and the experiments of Monty (Reference Monty2005), with up to
$y^{+}/{\it\beta}$
from (3.4) using the experimental and DNS data mentioned above and the experiments of Monty (Reference Monty2005), with up to
![]() $\mathit{Re}_{{\it\tau}}=3945$
, to determine a Reynolds-number-dependent value of the parameters. When evaluated for
$\mathit{Re}_{{\it\tau}}=3945$
, to determine a Reynolds-number-dependent value of the parameters. When evaluated for
![]() $\mathit{Re}_{{\it\tau}}=5186$
, these yield the parameter values shown in table 2.
$\mathit{Re}_{{\it\tau}}=5186$
, these yield the parameter values shown in table 2.
These two higher-order truncations have also been fitted to the LM5200 data to obtain values shown in table 2 that are significantly different from the previously determined values. The expressions for
![]() ${\it\beta}$
from (3.3) and (3.4) are plotted in figure 3(c) with both sets of parameters. It is clear from this figure that the parameter values obtained by Jiménez & Moser (Reference Jiménez and Moser2007) and Mizuno & Jiménez (Reference Mizuno and Jiménez2011) do not fit the LM5200 data, but the parameters fitted to the LM5200 data in the log region match the data equally well for both truncation forms. The reason for this disagreement with the parameters from Jiménez & Moser (Reference Jiménez and Moser2007) is clear, since the Reynolds numbers used in that study were not high enough to exhibit the logarithmic region observed in LM5200, since
${\it\beta}$
from (3.3) and (3.4) are plotted in figure 3(c) with both sets of parameters. It is clear from this figure that the parameter values obtained by Jiménez & Moser (Reference Jiménez and Moser2007) and Mizuno & Jiménez (Reference Mizuno and Jiménez2011) do not fit the LM5200 data, but the parameters fitted to the LM5200 data in the log region match the data equally well for both truncation forms. The reason for this disagreement with the parameters from Jiménez & Moser (Reference Jiménez and Moser2007) is clear, since the Reynolds numbers used in that study were not high enough to exhibit the logarithmic region observed in LM5200, since
![]() $y/{\it\delta}=0.16$
is at
$y/{\it\delta}=0.16$
is at
![]() $y^{+}=320$
when
$y^{+}=320$
when
![]() $\mathit{Re}_{{\it\tau}}=2000$
. They appear to have been fitting (3.3) to the outer-layer profile, and indeed in LM5200 there is a region
$\mathit{Re}_{{\it\tau}}=2000$
. They appear to have been fitting (3.3) to the outer-layer profile, and indeed in LM5200 there is a region
![]() $0.16<y/{\it\delta}<0.45$
in which
$0.16<y/{\it\delta}<0.45$
in which
![]() ${\it\beta}$
is approximately linear in
${\it\beta}$
is approximately linear in
![]() $y^{+}/\mathit{Re}_{{\it\tau}}$
, with a slope of one (figure 3
b), in agreement with
$y^{+}/\mathit{Re}_{{\it\tau}}$
, with a slope of one (figure 3
b), in agreement with
![]() ${\it\alpha}_{2}=1.0$
.
${\it\alpha}_{2}=1.0$
.
In contrast, the data used by Mizuno & Jiménez (Reference Mizuno and Jiménez2011) included a channel Reynolds number as high as
![]() $\mathit{Re}_{{\it\tau}}=3945$
, which should have exhibited a short nearly constant
$\mathit{Re}_{{\it\tau}}=3945$
, which should have exhibited a short nearly constant
![]() ${\it\beta}$
plateau as observed in LM5200. This would have been qualitatively different from the lower-Reynolds-number cases. This was not reported in that paper. However, at this Reynolds number, the plotted values of
${\it\beta}$
plateau as observed in LM5200. This would have been qualitatively different from the lower-Reynolds-number cases. This was not reported in that paper. However, at this Reynolds number, the plotted values of
![]() ${\it\kappa}$
and
${\it\kappa}$
and
![]() $a_{1}$
(figure 5 in Mizuno & Jiménez Reference Mizuno and Jiménez2011) are significantly larger than the parameters for lower Reynolds number. Further, the values for all three parameters obtained from the LM5200 data are within the indicated uncertainties of the parameters from the
$a_{1}$
(figure 5 in Mizuno & Jiménez Reference Mizuno and Jiménez2011) are significantly larger than the parameters for lower Reynolds number. Further, the values for all three parameters obtained from the LM5200 data are within the indicated uncertainties of the parameters from the
![]() $\mathit{Re}_{{\it\tau}}=3945$
experimental data. Perhaps the reported Reynolds number dependence of the parameters did not reflect a qualitative change at the highest Reynolds number, because the fit was dominated by the more numerous lower-Reynolds-number cases.
$\mathit{Re}_{{\it\tau}}=3945$
experimental data. Perhaps the reported Reynolds number dependence of the parameters did not reflect a qualitative change at the highest Reynolds number, because the fit was dominated by the more numerous lower-Reynolds-number cases.
The apparent extent of the overlap region in the LM5200 case is not sufficient to distinguish between the two asymptotic truncations, (3.3) and (3.4). Because
![]() $a_{1}$
is so small, the primary distinction is in the lowest non-zero exponent on
$a_{1}$
is so small, the primary distinction is in the lowest non-zero exponent on
![]() $y^{+}/\mathit{Re}_{{\it\tau}}$
. This may be of some importance because it determines the way in which the high-Reynolds-number asymptote of constant
$y^{+}/\mathit{Re}_{{\it\tau}}$
. This may be of some importance because it determines the way in which the high-Reynolds-number asymptote of constant
![]() ${\it\beta}$
is approached. Unfortunately, this cannot be determined using the available data.
${\it\beta}$
is approached. Unfortunately, this cannot be determined using the available data.
3.2. Reynolds stress tensor
The non-zero components of the Reynolds stress tensor (the velocity component variances and covariance) from the simulations and experiments are shown in figures 4–6. These figures show that there are some subtle inconsistencies among the three highest-Reynolds-number simulations (solid lines in the figures) and the experimental data.

Figure 4. Variance of
![]() $u$
: (a) as a function of
$u$
: (a) as a function of
![]() $y^{+}$
; (b) zoom of (a) near the peak; (c) dependence of maximum on
$y^{+}$
; (b) zoom of (a) near the peak; (c) dependence of maximum on
![]() $\mathit{Re}_{{\it\tau}}$
; solid line, relation (3.5); MWT, boundary layer in the Melbourne Wind Tunnel (Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009; Kulandaivelu Reference Kulandaivelu2011); PSP, Princeton Superpipe (Hultmark, Bailey & Smits Reference Hultmark, Bailey and Smits2010; Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012); (d) as a function of
$\mathit{Re}_{{\it\tau}}$
; solid line, relation (3.5); MWT, boundary layer in the Melbourne Wind Tunnel (Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009; Kulandaivelu Reference Kulandaivelu2011); PSP, Princeton Superpipe (Hultmark, Bailey & Smits Reference Hultmark, Bailey and Smits2010; Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012); (d) as a function of
![]() $y/{\it\delta}$
; (e) test function for Townsend’s prediction; (f) zoom of (d) near the centre of the channel. The linestyle and symbol legend is given in table 1.
$y/{\it\delta}$
; (e) test function for Townsend’s prediction; (f) zoom of (d) near the centre of the channel. The linestyle and symbol legend is given in table 1.

Figure 5. Variance of
![]() $v$
(a) and covariance of
$v$
(a) and covariance of
![]() $u$
and
$u$
and
![]() $v$
(b). The linestyle and symbol legend is given in table 1.
$v$
(b). The linestyle and symbol legend is given in table 1.
First, the two cases LJ4200 and BPO4100 are nearly identical in Reynolds number, but all three velocity variances are different between the two cases. The peak of the streamwise variance (figure 4
b) is approximately 1.4 % larger in LJ4200 than in BPO4100. The peak varies with Reynolds number, as can be seen in the figure, but this variation is logarithmic, and is too weak to explain the difference. Using the simulations LM1000, HJ2000 and LM5200, the dependence of the peak in
![]() $\langle u^{\prime 2}\rangle ^{+}$
on
$\langle u^{\prime 2}\rangle ^{+}$
on
![]() $\mathit{Re}_{{\it\tau}}$
was fitted to obtain
$\mathit{Re}_{{\it\tau}}$
was fitted to obtain
with
![]() $R^{2}=0.9995$
. This agrees well with the relationship
$R^{2}=0.9995$
. This agrees well with the relationship
![]() $\langle u^{\prime 2}\rangle _{max}^{+}=3.63+0.65\log (\mathit{Re}_{{\it\tau}})$
suggested by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014). The relationship (3.5) is plotted in figure 4(c) along with the values of the actual peaks, including those for LJ4200 and BPO4100. It is clear from this plot that the peak in BPO4100 is smaller than this relationship implies for
$\langle u^{\prime 2}\rangle _{max}^{+}=3.63+0.65\log (\mathit{Re}_{{\it\tau}})$
suggested by Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014). The relationship (3.5) is plotted in figure 4(c) along with the values of the actual peaks, including those for LJ4200 and BPO4100. It is clear from this plot that the peak in BPO4100 is smaller than this relationship implies for
![]() $\mathit{Re}_{{\it\tau}}=4100$
, while the peak from LJ4200 is consistent.
$\mathit{Re}_{{\it\tau}}=4100$
, while the peak from LJ4200 is consistent.
Also shown in figure 4(c) are experimental data for pipe flow by Hultmark et al. (Reference Hultmark, Bailey and Smits2010, Reference Hultmark, Vallikivi, Bailey and Smits2012), which indicate that the inner-peak value of
![]() $\langle u^{\prime 2}\rangle ^{+}$
does not continue to increase with
$\langle u^{\prime 2}\rangle ^{+}$
does not continue to increase with
![]() $\mathit{Re}$
for
$\mathit{Re}$
for
![]() $\mathit{Re}_{{\it\tau}}>5000$
. However, experimental data from boundary layers by Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) and Kulandaivelu (Reference Kulandaivelu2011) do not show such a growth saturation. The Reynolds numbers of the current simulations are unfortunately not high enough to determine whether the growth of
$\mathit{Re}_{{\it\tau}}>5000$
. However, experimental data from boundary layers by Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) and Kulandaivelu (Reference Kulandaivelu2011) do not show such a growth saturation. The Reynolds numbers of the current simulations are unfortunately not high enough to determine whether the growth of
![]() $\langle u^{\prime 2}\rangle ^{+}$
will saturate in channel flows. Also remarkable in figure 4(c) is how much lower the peak values are in the boundary layer data. This is probably due to the resolution of the measurements (Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009).
$\langle u^{\prime 2}\rangle ^{+}$
will saturate in channel flows. Also remarkable in figure 4(c) is how much lower the peak values are in the boundary layer data. This is probably due to the resolution of the measurements (Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009).
In other
![]() $y^{+}$
intervals (
$y^{+}$
intervals (
![]() $y^{+}<8$
and
$y^{+}<8$
and
![]() $25<y^{+}<200$
), the variance in the lower-Reynolds-number case (BPO4100) is actually greater than the variance in the higher-Reynolds-number flow (LJ4200). This appears to be inconsistent with the Reynolds number trends among the other cases, for which
$25<y^{+}<200$
), the variance in the lower-Reynolds-number case (BPO4100) is actually greater than the variance in the higher-Reynolds-number flow (LJ4200). This appears to be inconsistent with the Reynolds number trends among the other cases, for which
![]() $\langle u^{\prime 2}\rangle ^{+}$
increases monotonically with Reynolds number at constant
$\langle u^{\prime 2}\rangle ^{+}$
increases monotonically with Reynolds number at constant
![]() $y^{+}$
. Another inconsistency is apparent when the streamwise velocity variance is examined as a function of
$y^{+}$
. Another inconsistency is apparent when the streamwise velocity variance is examined as a function of
![]() $y/{\it\delta}$
(figure 4
d, f). Near the centreline (
$y/{\it\delta}$
(figure 4
d, f). Near the centreline (
![]() $y/{\it\delta}=1$
), the variance from LJ4200 is significantly larger than from both BPO4100 and LM5200, while the other simulations indicate that the variance should be increasing slowly with Reynolds number. It appears that far from the wall, LJ4200 is affected by its relatively small domain size, as might be expected. Finally, the experimental data with reported uncertainty,
$y/{\it\delta}=1$
), the variance from LJ4200 is significantly larger than from both BPO4100 and LM5200, while the other simulations indicate that the variance should be increasing slowly with Reynolds number. It appears that far from the wall, LJ4200 is affected by its relatively small domain size, as might be expected. Finally, the experimental data with reported uncertainty,
![]() $\pm 2\,\%$
, from SF4000 in figure 4(a) are inconsistent with LJ4200 and BPO4100 in the region near the wall (
$\pm 2\,\%$
, from SF4000 in figure 4(a) are inconsistent with LJ4200 and BPO4100 in the region near the wall (
![]() $y^{+}<300$
say). The reason for this discrepancy is not clear, but it may be due to the difficulty of measuring velocity fluctuations near the wall. Far from the wall, the experimental data for these quantities are consistent with the simulations. Measurements are not available at small enough
$y^{+}<300$
say). The reason for this discrepancy is not clear, but it may be due to the difficulty of measuring velocity fluctuations near the wall. Far from the wall, the experimental data for these quantities are consistent with the simulations. Measurements are not available at small enough
![]() $y^{+}$
to compare peak values of
$y^{+}$
to compare peak values of
![]() $\langle u^{\prime 2}\rangle ^{+}$
.
$\langle u^{\prime 2}\rangle ^{+}$
.
Similar inconsistencies are present among the high-Reynolds-number simulation cases in the wall-normal and spanwise velocity variances. Around the peaks of both
![]() $\langle v^{\prime 2}\rangle ^{+}$
and
$\langle v^{\prime 2}\rangle ^{+}$
and
![]() $\langle w^{\prime 2}\rangle ^{+}$
, BPO4100 exceeds values from LJ4200, despite its somewhat lower Reynolds number (figures 5
a and 6
a), while near the centre, these two cases are in agreement. Only the Reynolds shear stress
$\langle w^{\prime 2}\rangle ^{+}$
, BPO4100 exceeds values from LJ4200, despite its somewhat lower Reynolds number (figures 5
a and 6
a), while near the centre, these two cases are in agreement. Only the Reynolds shear stress
![]() $\langle u^{\prime }v^{\prime }\rangle ^{+}$
is in agreement in these cases across all
$\langle u^{\prime }v^{\prime }\rangle ^{+}$
is in agreement in these cases across all
![]() $y$
(figure 5
b). Similarly to
$y$
(figure 5
b). Similarly to
![]() $\langle u^{\prime 2}\rangle ^{+}$
, the experimental data from SF4000 for
$\langle u^{\prime 2}\rangle ^{+}$
, the experimental data from SF4000 for
![]() $\langle v^{\prime 2}\rangle ^{+}$
and
$\langle v^{\prime 2}\rangle ^{+}$
and
![]() $\langle u^{\prime }v^{\prime }\rangle ^{+}$
with uncertainties of
$\langle u^{\prime }v^{\prime }\rangle ^{+}$
with uncertainties of
![]() $\pm 3\,\%$
and
$\pm 3\,\%$
and
![]() $\pm 5\,\%$
respectively, are inconsistent with both simulations in the region near the wall, where the experimental data appear to be quite noisy. Possible reasons for the minor inconsistencies noted among the DNS are discussed in § 3.3.
$\pm 5\,\%$
respectively, are inconsistent with both simulations in the region near the wall, where the experimental data appear to be quite noisy. Possible reasons for the minor inconsistencies noted among the DNS are discussed in § 3.3.

Figure 6. Variance of
![]() $w$
(a) as a function of
$w$
(a) as a function of
![]() $y^{+}$
, (b) as a function of
$y^{+}$
, (b) as a function of
![]() $y/{\it\delta}$
, and test function for Townsend’s prediction (c) as a function of
$y/{\it\delta}$
, and test function for Townsend’s prediction (c) as a function of
![]() $y^{+}$
, (d) as a function of
$y^{+}$
, (d) as a function of
![]() $y/{\it\delta}$
. The linestyle and symbol legend is given in table 1.
$y/{\it\delta}$
. The linestyle and symbol legend is given in table 1.
There are several anticipated high-Reynolds-number features to be examined in the data. In particular, similarly to the log law, Townsend’s attached-eddy hypothesis (Townsend Reference Townsend1976) implies that in the high-Reynolds-number limit, there is an interval in
![]() $y$
in which the Reynolds stress components satisfy
$y$
in which the Reynolds stress components satisfy
is known analytically (
![]() ${\it\tau}_{tot}^{+}=1-y/{\it\delta}$
) from the mean momentum equation, and because
${\it\tau}_{tot}^{+}=1-y/{\it\delta}$
) from the mean momentum equation, and because
![]() ${\it\beta}$
varies little over a broad range of
${\it\beta}$
varies little over a broad range of
![]() $y$
(
$y$
(
![]() ${\it\beta}=2.6\pm 0.4\approx 1/{\it\kappa}$
for
${\it\beta}=2.6\pm 0.4\approx 1/{\it\kappa}$
for
![]() $30<y^{+}<0.75\mathit{Re}_{{\it\tau}}$
) (see figure 3), the variation with Reynolds number of the Reynolds shear stress near its maximum can be deduced easily:
$30<y^{+}<0.75\mathit{Re}_{{\it\tau}}$
) (see figure 3), the variation with Reynolds number of the Reynolds shear stress near its maximum can be deduced easily:
From this it is clear that the maximum Reynolds shear stress is given by
![]() ${\it\tau}_{RSmax}\approx 1-2/\sqrt{{\it\kappa}\mathit{Re }_{{\it\tau}}}$
, and that this maximum occurs at
${\it\tau}_{RSmax}\approx 1-2/\sqrt{{\it\kappa}\mathit{Re }_{{\it\tau}}}$
, and that this maximum occurs at
![]() $y^{+}\approx \sqrt{\mathit{Re }_{{\it\tau}}/{\it\kappa}}$
, as noted by Afzal (Reference Afzal1982), Morrison et al. (Reference Morrison, McKeon, Jiang and Smits2004), Panton (Reference Panton2007) and Sillero et al. (Reference Sillero, Jiménez and Moser2013). For the conditions of LM5200 (
$y^{+}\approx \sqrt{\mathit{Re }_{{\it\tau}}/{\it\kappa}}$
, as noted by Afzal (Reference Afzal1982), Morrison et al. (Reference Morrison, McKeon, Jiang and Smits2004), Panton (Reference Panton2007) and Sillero et al. (Reference Sillero, Jiménez and Moser2013). For the conditions of LM5200 (
![]() $\mathit{Re}_{{\it\tau}}=5186$
,
$\mathit{Re}_{{\it\tau}}=5186$
,
![]() ${\it\kappa}=0.384$
), these estimates yield
${\it\kappa}=0.384$
), these estimates yield
![]() ${\it\tau}_{RSmax}\approx 0.955$
occurring at
${\it\tau}_{RSmax}\approx 0.955$
occurring at
![]() $y^{+}\approx 116$
, in good agreement with the simulations. Further, the error in satisfying
$y^{+}\approx 116$
, in good agreement with the simulations. Further, the error in satisfying
![]() ${\it\tau}_{RS}=1$
is less than
${\it\tau}_{RS}=1$
is less than
![]() ${\it\epsilon}$
for a range of
${\it\epsilon}$
for a range of
![]() $y^{+}$
that increases in size like
$y^{+}$
that increases in size like
![]() ${\it\epsilon}\mathit{Re}_{{\it\tau}}$
for large
${\it\epsilon}\mathit{Re}_{{\it\tau}}$
for large
![]() $\mathit{Re}_{{\it\tau}}$
. Precisely,
$\mathit{Re}_{{\it\tau}}$
. Precisely,
Thus, for
![]() ${\it\tau}_{RS}$
to be within 5 % of one over a decade of variation of
${\it\tau}_{RS}$
to be within 5 % of one over a decade of variation of
![]() $y^{+}$
would require more than twice the Reynolds number of LM5200, and for it to be within 1 % at its peak requires 20 times greater Reynolds number.
$y^{+}$
would require more than twice the Reynolds number of LM5200, and for it to be within 1 % at its peak requires 20 times greater Reynolds number.
According to (3.6), both the variance of
![]() $u$
and the variance of
$u$
and the variance of
![]() $w$
would have a logarithmic variation over some region of
$w$
would have a logarithmic variation over some region of
![]() $y$
. In figure 6, it appears that there is such a logarithmic variation, even at Reynolds numbers as low as
$y$
. In figure 6, it appears that there is such a logarithmic variation, even at Reynolds numbers as low as
![]() $\mathit{Re}_{{\it\tau}}=1000$
. The indicator function
$\mathit{Re}_{{\it\tau}}=1000$
. The indicator function
![]() $y\partial _{y}\langle w^{\prime 2}\rangle$
is approximately flat from
$y\partial _{y}\langle w^{\prime 2}\rangle$
is approximately flat from
![]() $y^{+}\approx 100$
to
$y^{+}\approx 100$
to
![]() $y^{+}\approx 200$
(figure 6
c). The corresponding curve fit is
$y^{+}\approx 200$
(figure 6
c). The corresponding curve fit is
![]() $\langle w^{\prime 2}\rangle ^{+}=1.08-0.387\log (y/{\it\delta})$
, which is somewhat different from the fit
$\langle w^{\prime 2}\rangle ^{+}=1.08-0.387\log (y/{\it\delta})$
, which is somewhat different from the fit
![]() $\langle w^{\prime 2}\rangle ^{+}=0.8-0.45\log (y/{\it\delta})$
obtained by Sillero et al. (Reference Sillero, Jiménez and Moser2013) in a boundary layer DNS. On the other hand, there is no apparent logarithmic region in the
$\langle w^{\prime 2}\rangle ^{+}=0.8-0.45\log (y/{\it\delta})$
obtained by Sillero et al. (Reference Sillero, Jiménez and Moser2013) in a boundary layer DNS. On the other hand, there is no apparent logarithmic region in the
![]() $\langle u^{\prime 2}\rangle ^{+}$
profiles. The indicator function
$\langle u^{\prime 2}\rangle ^{+}$
profiles. The indicator function
![]() $y\partial _{y}\langle u^{\prime 2}\rangle ^{+}$
(figure 4
e) is not flat anywhere in the domain. There is, however, a region (
$y\partial _{y}\langle u^{\prime 2}\rangle ^{+}$
(figure 4
e) is not flat anywhere in the domain. There is, however, a region (
![]() $200<y^{+}<0.6\mathit{Re}_{{\it\tau}}$
) where the dependence of the indicator function on
$200<y^{+}<0.6\mathit{Re}_{{\it\tau}}$
) where the dependence of the indicator function on
![]() $y$
is linear with relatively small slope, and the slope may be decreasing with Reynolds number, though extremely slowly. In contrast, Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) observed a logarithmic region in
$y$
is linear with relatively small slope, and the slope may be decreasing with Reynolds number, though extremely slowly. In contrast, Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013) observed a logarithmic region in
![]() $\langle u^{\prime 2}\rangle ^{+}$
over the range
$\langle u^{\prime 2}\rangle ^{+}$
over the range
![]() $800<y^{+}<0.15\mathit{Re}_{{\it\tau}}$
in pipe flow with
$800<y^{+}<0.15\mathit{Re}_{{\it\tau}}$
in pipe flow with
![]() $\mathit{Re}_{{\it\tau}}>2\times 10^{4}$
. The LM5200 simulation is not at high enough Reynolds number to exhibit such a region if it occurs over the same range in
$\mathit{Re}_{{\it\tau}}>2\times 10^{4}$
. The LM5200 simulation is not at high enough Reynolds number to exhibit such a region if it occurs over the same range in
![]() $y$
, since
$y$
, since
![]() $0.15\mathit{Re}_{{\it\tau}}<800$
at
$0.15\mathit{Re}_{{\it\tau}}<800$
at
![]() $\mathit{Re}_{{\it\tau}}=5186$
.
$\mathit{Re}_{{\it\tau}}=5186$
.

Figure 7. Balance of production and dissipation of turbulent kinetic energy.
As mentioned in § 2, the terms in the Reynolds stress transport equations are not reported here, though the data are available at http://turbulence.ices.utexas.edu. Of interest here, however, is the transport equation for the turbulent kinetic energy
![]() $K=\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
. Hinze (Reference Hinze1975) argues that at sufficiently high Reynolds number, there is an intermediate region between inner and outer layers where the transport terms in the kinetic energy equation are small compared with production, so that in this region
$K=\langle u_{i}^{\prime }u_{i}^{\prime }\rangle /2$
. Hinze (Reference Hinze1975) argues that at sufficiently high Reynolds number, there is an intermediate region between inner and outer layers where the transport terms in the kinetic energy equation are small compared with production, so that in this region
where
![]() $P_{K}$
is the production of kinetic energy and
$P_{K}$
is the production of kinetic energy and
![]() ${\it\epsilon}$
is the dissipation. In the formulation and analysis of turbulence models, (3.10) is often assumed to hold in an overlap region between inner and outer layers (Durbin & Pettersson Reif Reference Durbin and Pettersson Reif2010). The relative error in the balance of production and dissipation (
${\it\epsilon}$
is the dissipation. In the formulation and analysis of turbulence models, (3.10) is often assumed to hold in an overlap region between inner and outer layers (Durbin & Pettersson Reif Reference Durbin and Pettersson Reif2010). The relative error in the balance of production and dissipation (
![]() $P_{K}/{\it\epsilon}-1$
) for LM1000, HJ2000 and LM5200 is shown in figure 7. In all three cases, there is a region
$P_{K}/{\it\epsilon}-1$
) for LM1000, HJ2000 and LM5200 is shown in figure 7. In all three cases, there is a region
![]() $y^{+}>30$
and
$y^{+}>30$
and
![]() $y/{\it\delta}<0.6$
in which the mismatch between production and dissipation is of order 10 % or less, but there is no indication that the magnitude of this mismatch is decreasing with Reynolds number. Indeed, there appears to be a stable structure with a local minimum in
$y/{\it\delta}<0.6$
in which the mismatch between production and dissipation is of order 10 % or less, but there is no indication that the magnitude of this mismatch is decreasing with Reynolds number. Indeed, there appears to be a stable structure with a local minimum in
![]() $P_{K}/{\it\epsilon}$
around
$P_{K}/{\it\epsilon}$
around
![]() $y^{+}=60$
and a local maximum around
$y^{+}=60$
and a local maximum around
![]() $y^{+}=300$
followed by a gradual decline towards
$y^{+}=300$
followed by a gradual decline towards
![]() $P_{K}/{\it\epsilon}=1$
with increasing
$P_{K}/{\it\epsilon}=1$
with increasing
![]() $y$
. Presumably this decline will become more gradual with increasing Reynolds number as
$y$
. Presumably this decline will become more gradual with increasing Reynolds number as
![]() $y/{\it\delta}=0.6$
increases in
$y/{\it\delta}=0.6$
increases in
![]() $y^{+}$
.
$y^{+}$
.
3.3. Discrepancies between simulations
In §§ 3.1 and 3.2, it was shown that the LM5200 simulation has differences from the two somewhat lower-Reynolds-number DNS LJ4200 and BPO4100, with discrepancies among all three simulations larger than expected given the Reynolds number differences and likely statistical errors. In the case of LJ4200, the reason for the differences from LM5200 is most likely the small domain size of LJ4200 (four and three times smaller in the streamwise and spanwise directions respectively). Indeed, Lozano-Durán & Jiménez (Reference Lozano-Durán and Jiménez2014) investigated the effects of the small domain size at
![]() $\mathit{Re}_{{\it\tau}}\approx 950$
by comparing with DNS in a domain consistent with the simulations reported here. Consistent with observations in § 3.2, they observed discrepancies in the velocity variances for
$\mathit{Re}_{{\it\tau}}\approx 950$
by comparing with DNS in a domain consistent with the simulations reported here. Consistent with observations in § 3.2, they observed discrepancies in the velocity variances for
![]() $y/{\it\delta}<0.25$
.
$y/{\it\delta}<0.25$
.
The differences between BPO4100 and both LJ4200 and LM5200 occur primarily in the near-wall region, as shown in § 3.2. It seems likely that these differences are due to numerical resolution limitations of BPO4100. As indicated in table 1, the grid spacing in BPO4100 is approximately the same as LM5200 in the spanwise direction and approximately 25 % finer in the streamwise direction. However, in BPO4100 a second-order finite difference approximation is used rather than the spectral method used in the simulations reported here. The effective resolution of such low-order schemes is significantly less at the same grid spacing. One way to see this is to consider the error incurred when differentiating a sine function of different wavenumbers, which is given by
![]() ${\it\epsilon}(k)=1-\sin (k{\it\Delta})/k{\it\Delta}$
. If one insists on limiting error to no more than 10 % (for example), then the wavenumber needs to be limited to one fourth of the highest wavenumber that can be represented on the grid. Thus, at this level of error, the finite difference approximation of the derivative has four times coarser effective resolution than a spectral method on the same grid.
${\it\epsilon}(k)=1-\sin (k{\it\Delta})/k{\it\Delta}$
. If one insists on limiting error to no more than 10 % (for example), then the wavenumber needs to be limited to one fourth of the highest wavenumber that can be represented on the grid. Thus, at this level of error, the finite difference approximation of the derivative has four times coarser effective resolution than a spectral method on the same grid.
Of course, there is much more to solving the Navier–Stokes equations than representing the derivative, and an appropriate error limit for the derivative is not clear. Nonetheless, in DNS, a common rule of thumb is that second-order finite difference has between two and four times coarser effective resolution than a Fourier spectral method on the same grid. In a study of the effects of resolution in DNS of low-Reynolds-number (
![]() $\mathit{Re}_{{\it\tau}}=180$
) channel flow, Oliver et al. (Reference Oliver, Malaya, Ulerich and Moser2014) found that with the Fourier/B-spline numerical representation used here, coarsening the resolution by a factor of two relative to the nominal resolution (nominal is comparable in wall units to that used for LM5200) results in changes of several per cent in the velocity variances near the wall. Further, Vreman & Kuerten (Reference Vreman and Kuerten2014) investigated differences between DNS using a Fourier–Chebyshev spectral method and DNS using a fourth-order staggered finite difference method, which is higher order and higher resolution than the method used for BPO4100. They reported a 1 % lower peak root-mean-square (r.m.s.)
$\mathit{Re}_{{\it\tau}}=180$
) channel flow, Oliver et al. (Reference Oliver, Malaya, Ulerich and Moser2014) found that with the Fourier/B-spline numerical representation used here, coarsening the resolution by a factor of two relative to the nominal resolution (nominal is comparable in wall units to that used for LM5200) results in changes of several per cent in the velocity variances near the wall. Further, Vreman & Kuerten (Reference Vreman and Kuerten2014) investigated differences between DNS using a Fourier–Chebyshev spectral method and DNS using a fourth-order staggered finite difference method, which is higher order and higher resolution than the method used for BPO4100. They reported a 1 % lower peak root-mean-square (r.m.s.)
![]() $u^{\prime }$
for the fourth-order method. These results indicate that the lower effective resolution in BPO4100 relative to LM5200 is a plausible cause of the minor inconsistencies between these two simulations. To determine this definitively it would be necessary to redo the BPO4100 simulation with twice the resolution in each direction, or more, which is out of the scope of the current study.
$u^{\prime }$
for the fourth-order method. These results indicate that the lower effective resolution in BPO4100 relative to LM5200 is a plausible cause of the minor inconsistencies between these two simulations. To determine this definitively it would be necessary to redo the BPO4100 simulation with twice the resolution in each direction, or more, which is out of the scope of the current study.
3.4. Energy spectral density
One of the properties of high-Reynolds-number wall-bounded turbulence is the separation of scales between the near-wall and outer-layer turbulence. For the LM5200 case, this separation of scales can be seen in the one-dimensional velocity spectra. For example, the premultiplied spectral energy density of the streamwise velocity fluctuations is shown as a function of
![]() $y$
in figure 8. The premultiplied spectrum
$y$
in figure 8. The premultiplied spectrum
![]() $kE(k,y^{+})$
is the energy density per
$kE(k,y^{+})$
is the energy density per
![]() $\log k$
, and so, in the logarithmic wavenumber scale used in figure 8, it indicates the scales at which the energy resides. The energy spectral density of
$\log k$
, and so, in the logarithmic wavenumber scale used in figure 8, it indicates the scales at which the energy resides. The energy spectral density of
![]() $u$
in the streamwise direction has two distinct peaks, one at
$u$
in the streamwise direction has two distinct peaks, one at
![]() $k_{x}{\it\delta}=40$
,
$k_{x}{\it\delta}=40$
,
![]() $y^{+}=13$
and one at
$y^{+}=13$
and one at
![]() $k_{x}{\it\delta}=1$
,
$k_{x}{\it\delta}=1$
,
![]() $y^{+}=400$
. To the best of our knowledge, such distinct peaks have only previously been observed in high-Reynolds-number experimental data (Hutchins & Marusic Reference Hutchins and Marusic2007; Monty et al.
Reference Monty, Hutchins, Ng, Marusic and Chong2009; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010a
; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
). An even more vivid double peak is visible in the spanwise spectrum of
$y^{+}=400$
. To the best of our knowledge, such distinct peaks have only previously been observed in high-Reynolds-number experimental data (Hutchins & Marusic Reference Hutchins and Marusic2007; Monty et al.
Reference Monty, Hutchins, Ng, Marusic and Chong2009; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010a
; Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010b
). An even more vivid double peak is visible in the spanwise spectrum of
![]() $u$
(figure 8
b), with peaks at
$u$
(figure 8
b), with peaks at
![]() $k_{z}{\it\delta}=250$
,
$k_{z}{\it\delta}=250$
,
![]() $y^{+}=13$
and
$y^{+}=13$
and
![]() $k_{z}{\it\delta}=6$
,
$k_{z}{\it\delta}=6$
,
![]() $y^{+}=1000$
.
$y^{+}=1000$
.

Figure 8. Wavenumber-premultiplied energy spectral density from LM5200: (a)
![]() $k_{x}E_{uu}/u_{{\it\tau}}^{2}$
, (b)
$k_{x}E_{uu}/u_{{\it\tau}}^{2}$
, (b)
![]() $k_{z}E_{uu}/u_{{\it\tau}}^{2}$
, (c)
$k_{z}E_{uu}/u_{{\it\tau}}^{2}$
, (c)
![]() $-k_{x}E_{uv}/u_{{\it\tau}}^{2}$
, (d)
$-k_{x}E_{uv}/u_{{\it\tau}}^{2}$
, (d)
![]() $-k_{z}E_{uv}/u_{{\it\tau}}^{2}$
.
$-k_{z}E_{uv}/u_{{\it\tau}}^{2}$
.
Similarly, there are weak double peaks in the cospectrum of
![]() $uv$
, as shown in figure 8(c,d). In the LM5200 case, distinct inner and outer peaks were not observed in the spectral density of
$uv$
, as shown in figure 8(c,d). In the LM5200 case, distinct inner and outer peaks were not observed in the spectral density of
![]() $v^{2}$
and
$v^{2}$
and
![]() $w^{2}$
(not shown). It thus appears that it is primarily the streamwise velocity fluctuations that are exhibiting inner/outer scale separation at this Reynolds number.
$w^{2}$
(not shown). It thus appears that it is primarily the streamwise velocity fluctuations that are exhibiting inner/outer scale separation at this Reynolds number.
As mentioned earlier, the scaling analysis of Perry et al. (Reference Perry, Henbest and Chong1986) suggests that at high Reynolds number the energy spectral density of the streamwise velocity fluctuations varies as
![]() $k_{x}^{-1}$
in the overlap region where both inner and outer scaling are valid. However, until now, the
$k_{x}^{-1}$
in the overlap region where both inner and outer scaling are valid. However, until now, the
![]() $k_{x}^{-1}$
region has been elusive in simulations, presumably because the Reynolds numbers have not been high enough. It is only in high-Reynolds-number experiments (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005, Reference Nickels, Marusic, Hafez, Hutchins and Chong2007; Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013) that a
$k_{x}^{-1}$
region has been elusive in simulations, presumably because the Reynolds numbers have not been high enough. It is only in high-Reynolds-number experiments (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005, Reference Nickels, Marusic, Hafez, Hutchins and Chong2007; Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013) that a
![]() $k_{x}^{-1}$
region has previously been observed in the streamwise velocity spectrum. In the LM5200 simulation, the premultiplied energy spectral density does indeed exhibit a plateau in the region
$k_{x}^{-1}$
region has previously been observed in the streamwise velocity spectrum. In the LM5200 simulation, the premultiplied energy spectral density does indeed exhibit a plateau in the region
![]() $90\leqslant y^{+}\leqslant 170$
and
$90\leqslant y^{+}\leqslant 170$
and
![]() $6\leqslant k_{x}{\it\delta}\leqslant 10$
(figure 9
a). Further, the magnitude of the premultiplied spectrum at the plateau agrees with the value observed experimentally, approximately 0.8 in wall units, in boundary layers (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005) and in pipe flow (Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). However, the plateau in the experimental premultiplied spectrum in the pipe flow of Rosenberg et al. (Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013) is only observed for
$6\leqslant k_{x}{\it\delta}\leqslant 10$
(figure 9
a). Further, the magnitude of the premultiplied spectrum at the plateau agrees with the value observed experimentally, approximately 0.8 in wall units, in boundary layers (Nickels et al.
Reference Nickels, Marusic, Hafez and Chong2005) and in pipe flow (Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). However, the plateau in the experimental premultiplied spectrum in the pipe flow of Rosenberg et al. (Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013) is only observed for
![]() $\mathit{Re}_{{\it\tau}}\leqslant 3300$
. From the current results, we cannot determine whether the occurrence or extent of the plateau region might change at higher Reynolds number in channels.
$\mathit{Re}_{{\it\tau}}\leqslant 3300$
. From the current results, we cannot determine whether the occurrence or extent of the plateau region might change at higher Reynolds number in channels.

Figure 9. The
![]() $k^{-1}$
region: (a)
$k^{-1}$
region: (a)
![]() $k_{x}E_{uu}/u_{{\it\tau}}^{2}$
at
$k_{x}E_{uu}/u_{{\it\tau}}^{2}$
at
![]() $y^{+}=90{-}170$
, (b)
$y^{+}=90{-}170$
, (b)
![]() $k_{z}E_{uu}/u_{{\it\tau}}^{2}$
at
$k_{z}E_{uu}/u_{{\it\tau}}^{2}$
at
![]() $y^{+}=3{-}14$
, (c)
$y^{+}=3{-}14$
, (c)
![]() $k_{z}E_{uu}/u_{{\it\tau}}^{2}$
at
$k_{z}E_{uu}/u_{{\it\tau}}^{2}$
at
![]() $y^{+}=111{-}141$
.
$y^{+}=111{-}141$
.
A similar scaling analysis also suggests that there should be a plateau in the premultiplied spanwise spectrum, and indeed an even broader plateau appears for
![]() $5\leqslant k_{z}{\it\delta}\leqslant 30$
, as observed previously by Hoyas & Jiménez (Reference Hoyas and Jiménez2008) and Sillero et al. (Reference Sillero, Jiménez and Moser2013). Interestingly, the plateau also occurs in the viscous sublayer region (figure 9
b). In the viscous sublayer the streamwise velocity fluctuations are dominated by the well-known streaky structures, with a characteristic spacing of
$5\leqslant k_{z}{\it\delta}\leqslant 30$
, as observed previously by Hoyas & Jiménez (Reference Hoyas and Jiménez2008) and Sillero et al. (Reference Sillero, Jiménez and Moser2013). Interestingly, the plateau also occurs in the viscous sublayer region (figure 9
b). In the viscous sublayer the streamwise velocity fluctuations are dominated by the well-known streaky structures, with a characteristic spacing of
![]() ${\rm\Delta}z^{+}\approx 100$
. This is evidenced by the large high-wavenumber peaks in the spanwise spectra around
${\rm\Delta}z^{+}\approx 100$
. This is evidenced by the large high-wavenumber peaks in the spanwise spectra around
![]() $k_{z}/{\it\delta}\approx 300~(k_{z}^{+}\approx 2{\rm\pi}/{\rm\Delta}z^{+})$
. At much larger scales (much lower wavenumbers), the viscous layer is driven by the larger-scale turbulence further from the wall. The plateau in the spanwise premultiplied spectrum in the viscous layer is thus a reflection of the spectral plateau further from the wall (figure 9
c).
$k_{z}/{\it\delta}\approx 300~(k_{z}^{+}\approx 2{\rm\pi}/{\rm\Delta}z^{+})$
. At much larger scales (much lower wavenumbers), the viscous layer is driven by the larger-scale turbulence further from the wall. The plateau in the spanwise premultiplied spectrum in the viscous layer is thus a reflection of the spectral plateau further from the wall (figure 9
c).
Another experimentally observed feature of the streamwise premultiplied spectrum is the presence of two local maxima, with one peak occurring on either side of the plateau (Guala, Hommema & Adrian Reference Guala, Hommema and Adrian2006; Kunkel & Marusic Reference Kunkel and Marusic2006). However, this bimodal feature was called into question when it was noted that the low-wavenumber peak, which occurs at
![]() $k_{x}{\it\delta}$
of order one, is at low enough wavenumber to be affected by the use of Taylor’s hypothesis to infer the spatial spectrum from the measured temporal spectrum (Del Álamo & Jiménez Reference Del Álamo and Jiménez2009; Moin Reference Moin2009). Indeed, in the HJ2000 simulation, it was found that the streamwise spatial spectrum did not display a low-wavenumber peak, while a spectrum determined from a time series did (Del Álamo & Jiménez Reference Del Álamo and Jiménez2009). In the LM5200 case, this bimodal feature does occur, as can be seen in figure 9(a). However, it is not clear whether this is a general high-Reynolds-number feature, or whether it is characteristic of intermediate Reynolds numbers. From figure 8, it is clear that the high- and low-wavenumber peaks in
$k_{x}{\it\delta}$
of order one, is at low enough wavenumber to be affected by the use of Taylor’s hypothesis to infer the spatial spectrum from the measured temporal spectrum (Del Álamo & Jiménez Reference Del Álamo and Jiménez2009; Moin Reference Moin2009). Indeed, in the HJ2000 simulation, it was found that the streamwise spatial spectrum did not display a low-wavenumber peak, while a spectrum determined from a time series did (Del Álamo & Jiménez Reference Del Álamo and Jiménez2009). In the LM5200 case, this bimodal feature does occur, as can be seen in figure 9(a). However, it is not clear whether this is a general high-Reynolds-number feature, or whether it is characteristic of intermediate Reynolds numbers. From figure 8, it is clear that the high- and low-wavenumber peaks in
![]() $k_{x}E_{uu}(k_{x},y^{+})$
at around
$k_{x}E_{uu}(k_{x},y^{+})$
at around
![]() $y^{+}=100$
are simply the upper and lower edges of the near wall and outer peaks in
$y^{+}=100$
are simply the upper and lower edges of the near wall and outer peaks in
![]() $k_{x}E_{uu}(k_{x},y^{+})$
respectively. As the Reynolds number increases, the inner peak will move to larger
$k_{x}E_{uu}(k_{x},y^{+})$
respectively. As the Reynolds number increases, the inner peak will move to larger
![]() $k_{x}$
and the outer peak to larger
$k_{x}$
and the outer peak to larger
![]() $y^{+}$
. As the outer peak moves to larger
$y^{+}$
. As the outer peak moves to larger
![]() $y^{+}$
, it seems likely that the inner and outer peaks will not overlap at all in
$y^{+}$
, it seems likely that the inner and outer peaks will not overlap at all in
![]() $y$
, resulting in no bimodal premultiplied spectrum at any
$y$
, resulting in no bimodal premultiplied spectrum at any
![]() $y$
. For example, the peaks are better separated in the premultiplied spanwise spectrum, and there are no bimodal
$y$
. For example, the peaks are better separated in the premultiplied spanwise spectrum, and there are no bimodal
![]() $k_{z}$
premultiplied spectra (figure 9
b).
$k_{z}$
premultiplied spectra (figure 9
b).
4. Discussion and conclusion
The DNS of turbulent channel flow at
![]() $\mathit{Re}_{{\it\tau}}=5186$
that is reported here has been shown to be a reliable source of data on high-Reynolds-number wall-bounded turbulence, and a wealth of statistical data from this flow is available online at http://turbulence.ices.utexas.edu. In particular, the resolution is consistent with or better than accepted standards for wall-bounded turbulence DNS, statistical uncertainties are generally small (of order 1 % or less), statistical data are consistent with Reynolds-number trends in DNS at
$\mathit{Re}_{{\it\tau}}=5186$
that is reported here has been shown to be a reliable source of data on high-Reynolds-number wall-bounded turbulence, and a wealth of statistical data from this flow is available online at http://turbulence.ices.utexas.edu. In particular, the resolution is consistent with or better than accepted standards for wall-bounded turbulence DNS, statistical uncertainties are generally small (of order 1 % or less), statistical data are consistent with Reynolds-number trends in DNS at
![]() $\mathit{Re}_{{\it\tau}}\leqslant 2000$
, and with experimental data, within reasonable tolerance, and, finally, the flow is statistically stationary to high accuracy. Further, as recapped below, the simulation exhibits many characteristics of high-Reynolds-number wall-bounded turbulence, making this simulation a good resource for the study of such high-Reynolds-number flows. Several conclusions can thus be drawn about high-Reynolds-number turbulent channel flow, as discussed below.
$\mathit{Re}_{{\it\tau}}\leqslant 2000$
, and with experimental data, within reasonable tolerance, and, finally, the flow is statistically stationary to high accuracy. Further, as recapped below, the simulation exhibits many characteristics of high-Reynolds-number wall-bounded turbulence, making this simulation a good resource for the study of such high-Reynolds-number flows. Several conclusions can thus be drawn about high-Reynolds-number turbulent channel flow, as discussed below.
At high Reynolds number, it is expected that a region of logarithmic variation will exist in the mean velocity. The current simulation exhibits an unambiguous logarithmic region with von Kármán constant
![]() ${\it\kappa}=0.384\pm 0.004$
. This is the first such unambiguous simulated logarithmic profile that the authors are aware of. At high Reynolds number, it is also expected (Townsend Reference Townsend1976) that the variance of the velocity fluctuations will have a region of logarithmic variation. This was found to be true for the spanwise fluctuations, but not the streamwise fluctuations. Indeed, the streamwise variance shows no sign of converging towards a logarithmic variation with increasing Reynolds number. Finally, it is often assumed that at high Reynolds number the production of turbulent kinetic energy will locally balance its dissipation over some overlap region between inner and outer layers. However, this was observed only approximately in the current simulation, with 10 % accuracy and with no sign that this mismatch is declining with Reynolds number. This balance of production and dissipation thus appears to be just an imperfect approximation.
${\it\kappa}=0.384\pm 0.004$
. This is the first such unambiguous simulated logarithmic profile that the authors are aware of. At high Reynolds number, it is also expected (Townsend Reference Townsend1976) that the variance of the velocity fluctuations will have a region of logarithmic variation. This was found to be true for the spanwise fluctuations, but not the streamwise fluctuations. Indeed, the streamwise variance shows no sign of converging towards a logarithmic variation with increasing Reynolds number. Finally, it is often assumed that at high Reynolds number the production of turbulent kinetic energy will locally balance its dissipation over some overlap region between inner and outer layers. However, this was observed only approximately in the current simulation, with 10 % accuracy and with no sign that this mismatch is declining with Reynolds number. This balance of production and dissipation thus appears to be just an imperfect approximation.
One of the most important characteristics of high-Reynolds-number wall-bounded turbulence is a distinct separation in scale between turbulence near the wall and far from the wall. This is observed in the streamwise and spanwise premultiplied spectral density of the streamwise velocity fluctuations and in the cospectrum of streamwise and wall-normal fluctuations. Moreover, a short
![]() $k^{-1}$
region is observed in the streamwise spectra and there is a wider region in the spanwise spectra, as predicted from scaling analysis (Perry et al.
Reference Perry, Henbest and Chong1986), and as observed experimentally. Finally, the bimodal structure in the premultiplied spectrum that has been observed experimentally (Guala et al.
Reference Guala, Hommema and Adrian2006; Kunkel & Marusic Reference Kunkel and Marusic2006) has also been observed here, despite suggestions that the experimental observations were an artefact of the use of Taylor’s hypothesis, which is not used here. However, it seems likely that this two-peak structure will not continue as the Reynolds number increases and the inner and outer peaks in the premultiplied spectra become further separated in
$k^{-1}$
region is observed in the streamwise spectra and there is a wider region in the spanwise spectra, as predicted from scaling analysis (Perry et al.
Reference Perry, Henbest and Chong1986), and as observed experimentally. Finally, the bimodal structure in the premultiplied spectrum that has been observed experimentally (Guala et al.
Reference Guala, Hommema and Adrian2006; Kunkel & Marusic Reference Kunkel and Marusic2006) has also been observed here, despite suggestions that the experimental observations were an artefact of the use of Taylor’s hypothesis, which is not used here. However, it seems likely that this two-peak structure will not continue as the Reynolds number increases and the inner and outer peaks in the premultiplied spectra become further separated in
![]() $k$
and
$k$
and
![]() $y$
.
$y$
.
Acknowledgements
The work presented here was supported by the National Science Foundation under award number (OCI-0749223) and the Argonne Leadership Computing Facility at Argonne National Laboratory under Early Science Program (ESP) and Innovative and Novel Computational Impact on Theory and Experiment Program (INCITE) 2013. We wish to thank N. Malaya and R. Ulerich for software engineering assistance. We are also thankful to M. P. Schultz and K. A. Flack for providing their experimental data.