Article contents
Direct numerical simulations of the flow around wings with spanwise waviness
Published online by Cambridge University Press: 10 August 2017
Abstract
The use of spanwise waviness in wings has been proposed in the literature as a possible mechanism for obtaining improved aerodynamic characteristics, motivated by the tubercles that cover the leading edge of the pectoral flippers of the humpback whale. We investigate the effect of this type of waviness on the incompressible flow around infinite wings with a NACA0012 profile, using direct numerical simulations employing the spectral/hp method. Simulations were performed for Reynolds numbers of 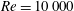 $Re=10\,000$ and
$Re=10\,000$ and 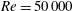 $Re=50\,000$ , considering different angles of attack in both the pre-stall and post-stall regimes. The results show that the waviness can either increase or decrease the lift coefficient, depending on the particular
$Re=50\,000$ , considering different angles of attack in both the pre-stall and post-stall regimes. The results show that the waviness can either increase or decrease the lift coefficient, depending on the particular 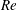 $Re$ and flow regime. We observe that the flow around the wavy wing exhibits a tendency to remain attached behind the waviness peak, with separation restricted to the troughs, which is consistent with results from the literature. Then, we identify three important physical mechanisms in this flow. The first mechanism is the weakening of the suction peak on the sections corresponding to the waviness peaks. This characteristic had been observed in a previous investigation for a very low Reynolds number of
$Re$ and flow regime. We observe that the flow around the wavy wing exhibits a tendency to remain attached behind the waviness peak, with separation restricted to the troughs, which is consistent with results from the literature. Then, we identify three important physical mechanisms in this flow. The first mechanism is the weakening of the suction peak on the sections corresponding to the waviness peaks. This characteristic had been observed in a previous investigation for a very low Reynolds number of 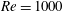 $Re=1000$ , and we show that this is still important even at
$Re=1000$ , and we show that this is still important even at 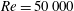 $Re=50\,000$ . As a second mechanism, the waviness has a significant effect on the stability of the separated shear layers, with transition occurring earlier for the wavy wing. In the pre-stall regime, for
$Re=50\,000$ . As a second mechanism, the waviness has a significant effect on the stability of the separated shear layers, with transition occurring earlier for the wavy wing. In the pre-stall regime, for 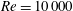 $Re=10\,000$ , the flow around the baseline wing is completely laminar, and the earlier transition leads to a large increase in the lift coefficient, while for
$Re=10\,000$ , the flow around the baseline wing is completely laminar, and the earlier transition leads to a large increase in the lift coefficient, while for 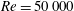 $Re=50\,000$ , the earlier transition leads to a shortening of the separation bubble which does not lead to an increased lift coefficient. The last mechanism corresponds to a sub-harmonic behaviour, with the flow being notably different between subsequent wavelengths. This allows the wing to maintain higher lift coefficients in some portions of the span.
$Re=50\,000$ , the earlier transition leads to a shortening of the separation bubble which does not lead to an increased lift coefficient. The last mechanism corresponds to a sub-harmonic behaviour, with the flow being notably different between subsequent wavelengths. This allows the wing to maintain higher lift coefficients in some portions of the span.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 48
- Cited by


