Article contents
Discrete-vortex method with novel shedding criterion for unsteady aerofoil flows with intermittent leading-edge vortex shedding
Published online by Cambridge University Press: 23 June 2014
Abstract
Unsteady aerofoil flows are often characterized by leading-edge vortex (LEV) shedding. While experiments and high-order computations have contributed to our understanding of these flows, fast low-order methods are needed for engineering tasks. Classical unsteady aerofoil theories are limited to small amplitudes and attached leading-edge flows. Discrete-vortex methods that model vortex shedding from leading edges assume continuous shedding, valid only for sharp leading edges, or shedding governed by ad-hoc criteria such as a critical angle of attack, valid only for a restricted set of kinematics. We present a criterion for intermittent vortex shedding from rounded leading edges that is governed by a maximum allowable leading-edge suction. We show that, when using unsteady thin aerofoil theory, this leading-edge suction parameter (LESP) is related to the 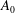 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A_0$ term in the Fourier series representing the chordwise variation of bound vorticity. Furthermore, for any aerofoil and Reynolds number, there is a critical value of the LESP, which is independent of the motion kinematics. When the instantaneous LESP value exceeds the critical value, vortex shedding occurs at the leading edge. We have augmented a discrete-time, arbitrary-motion, unsteady thin aerofoil theory with discrete-vortex shedding from the leading edge governed by the instantaneous LESP. Thus, the use of a single empirical parameter, the critical-LESP value, allows us to determine the onset, growth, and termination of LEVs. We show, by comparison with experimental and computational results for several aerofoils, motions and Reynolds numbers, that this computationally inexpensive method is successful in predicting the complex flows and forces resulting from intermittent LEV shedding, thus validating the LESP concept.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}A_0$ term in the Fourier series representing the chordwise variation of bound vorticity. Furthermore, for any aerofoil and Reynolds number, there is a critical value of the LESP, which is independent of the motion kinematics. When the instantaneous LESP value exceeds the critical value, vortex shedding occurs at the leading edge. We have augmented a discrete-time, arbitrary-motion, unsteady thin aerofoil theory with discrete-vortex shedding from the leading edge governed by the instantaneous LESP. Thus, the use of a single empirical parameter, the critical-LESP value, allows us to determine the onset, growth, and termination of LEVs. We show, by comparison with experimental and computational results for several aerofoils, motions and Reynolds numbers, that this computationally inexpensive method is successful in predicting the complex flows and forces resulting from intermittent LEV shedding, thus validating the LESP concept.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 232
- Cited by

