Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-21T04:47:28.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Drag reduction in numerical two-phase Taylor–Couette turbulence using an Euler–Lagrange approach

Published online by Cambridge University Press:  06 June 2016

Vamsi Spandan ,
Rodolfo Ostilla-Mónico ,
Roberto Verzicco  and
Detlef Lohse
Vamsi Spandan
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J. M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, Netherlands
Rodolfo Ostilla-Mónico
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J. M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J. M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, Netherlands Dipartimento di Ingegneria Meccanica, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Rome 00133, Italy
Detlef Lohse*
Affiliation:
Physics of Fluids Group, Faculty of Science and Technology, J. M. Burgers Center for Fluid Dynamics and MESA+ Institute, University of Twente, 7500 AE Enschede, Netherlands Max Planck Institute for Dynamics and Self-Organization, Göttingen 37077, Germany
*
†Email address for correspondence: d.lohse@utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

Two-phase turbulent Taylor–Couette (TC) flow is simulated using an Euler–Lagrange approach to study the effects of a secondary phase dispersed into a turbulent carrier phase (here bubbles dispersed into water). The dynamics of the carrier phase is computed using direct numerical simulations (DNS) in an Eulerian framework, while the bubbles are tracked in a Lagrangian manner by modelling the effective drag, lift, added mass and buoyancy force acting on them. Two-way coupling is implemented between the dispersed phase and the carrier phase which allows for momentum exchange among both phases and to study the effect of the dispersed phase on the carrier phase dynamics. The radius ratio of the TC setup is fixed to 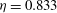${\it\eta}=0.833$, and a maximum inner cylinder Reynolds number of 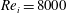$Re_{i}=8000$ is reached. We vary the Froude number (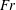$Fr$), which is the ratio of the centripetal to the gravitational acceleration of the dispersed phase and study its effect on the net torque required to drive the TC system. For the two-phase TC system, we observe drag reduction, i.e. the torque required to drive the inner cylinder is lower compared with that of the single-phase system. The net drag reduction decreases with increasing Reynolds number 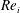$Re_{i}$, which is consistent with previous experimental findings (Murai et al., J. Phys.: Conf. Ser., vol. 14, 2005, pp. 143–156; Phys. Fluids, vol. 20(3), 2008, 034101). The drag reduction is strongly related to the Froude number: for fixed Reynolds number we observe higher drag reduction when 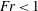$Fr<1$ than for with 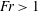$Fr>1$. This buoyancy effect is more prominent in low 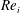$Re_{i}$ systems and decreases with increasing Reynolds number 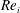$Re_{i}$. We trace the drag reduction back to the weakening of the angular momentum carrying Taylor rolls by the rising bubbles. We also investigate how the motion of the dispersed phase depends on 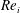$Re_{i}$ and 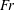$Fr$, by studying the individual trajectories and mean dispersion of bubbles in the radial and axial directions. Indeed, the less buoyant bubbles (large 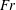$Fr$) tend to get trapped by the Taylor rolls, while the more buoyant bubbles (small 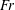$Fr$) rise through and weaken them.

JFM classification

Flow Control: Drag reduction Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 798 , 10 July 2016 , pp. 411 - 435
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Auton, T. R. 1987 The lift force on a spherical body in a rotational flow. J. Fluid Mech. 183, 199–218.CrossRefGoogle Scholar
Auton, T. R., Hunt, J. C. R. & Prud’Homme, M. 1988 The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 197, 241–257.Google Scholar
van den Berg, T. H., van Gils, D. P. M., Lathrop, D. P. & Lohse, D. 2007 Bubbly turbulent drag reduction is a boundary layer effect. Phys. Rev. Lett. 98 (8), 084501.CrossRefGoogle ScholarPubMed
van den Berg, T. H., Luther, S., Lathrop, D. P. & Lohse, D. 2005 Drag reduction in bubbly Taylor–Couette turbulence. Phys. Rev. Lett. 94 (4), 044501.Google Scholar
Capecelatro, J. & Desjardins, O. 2013 An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 238, 1–31.CrossRefGoogle Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.CrossRefGoogle Scholar
Chouippe, A., Climent, E., Legendre, D. & Gabillet, C. 2014 Numerical simulation of bubble dispersion in turbulent Taylor–Couette flow. Phys. Fluids 26 (4), 043304.CrossRefGoogle Scholar
Climent, E., Simonnet, M. & Magnaudet, J. 2007 Preferential accumulation of bubbles in Couette–Taylor flow patterns. Phys. Fluids 19 (8), 083301.Google Scholar
Dabiri, S., Lu, J. & Tryggvason, G. 2013 Transition between regimes of a vertical channel bubbly upflow due to bubble deformability. Phys. Fluids 25 (10), 102110.Google Scholar
Djeridi, H., Fave, J.-F., Billard, J.-Y. & Fruman, D. H. 1999 Bubble capture and migration in Couette–Taylor flow. Exp. Fluids 26, 233–239.Google Scholar
Djeridi, H., Gabillet, C. & Billard, J. Y. 2004 Two-phase Couette–Taylor flow: arrangement of the dispersed phase and effects on the flow structures. Phys. Fluids 16 (1), 128–139.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.Google Scholar
Fokoua, G. N., Gabillet, C., Aubert, A. & Colin, C. 2015 Effect of bubbles arrangement on the viscous torque in bubbly Taylor–Couette flow. Phys. Fluids 27 (3), 034105.Google Scholar
van Gils, D. P. M., Narezo Guzman, D., Sun, C. & Lohse, D. 2013 The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech. 722, 317–347.Google Scholar
Grossmann, S., Lohse, D. & Sun, C. 2016 High Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech. 48 (1), 53–80.Google Scholar
Harleman, M. J. W.2012 On the effect of turbulence on bubbles: experiments and numerical simulations of bubbles in wall-bounded flows. TU Delft, Delft University of Technology.Google Scholar
Jiménez, J. 2011 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44 (1), 27–45.Google Scholar
Lakkaraju, R., Toschi, F. & Lohse, D. 2014 Bubbling reduces intermittency in turbulent thermal convection. J. Fluid Mech. 745, 1–24.Google Scholar
Lu, J., Fernández, A. & Tryggvason, G. 2005 The effect of bubbles on the wall drag in a turbulent channel flow. Phys. Fluids 17 (9), 095102.Google Scholar
Lu, J. & Tryggvason, G. 2008 Effect of bubble deformability in turbulent bubbly upflow in a vertical channel. Phys. Fluids 20 (4), 040701.Google Scholar
L’vov, V. S., Pomyalov, A., Procaccia, I. & Tiberkevich, V. 2005 Drag reduction by microbubbles in turbulent flows: the limit of minute bubbles. Phys. Rev. Lett. 94 (17), 174502.CrossRefGoogle ScholarPubMed
Madavan, N. K., Deutsch, S. & Merkle, C. L.1983 Reduction of turbulent skin friction by microbubbles. Tech. Rep. DTIC Document.Google Scholar
Madavan, N. K., Deutsch, S. & Merkle, C. L. 1985 Measurements of local skin friction in a microbubble-modified turbulent boundary layer. J. Fluid Mech. 156, 237–256.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.Google Scholar
Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 The effect of microbubbles on developed turbulence. Phys. Fluids 15 (1), L5–L8.Google Scholar
Mei, R. & Klausner, J. F. 1992 Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids. 4 (1), 63–70.CrossRefGoogle Scholar
Murai, Y. 2014 Frictional drag reduction by bubble injection. Exp. Fluids 55 (7), 1–28.CrossRefGoogle Scholar
Murai, Y., Fukuda, H., Oishi, Y., Kodama, Y. & Yamamoto, F. 2007 Skin friction reduction by large air bubbles in a horizontal channel flow. Intl J. Multiphase Flow 33 (2), 147–163.Google Scholar
Murai, Y., Oiwa, H. & Takeda, Y. 2005 Bubble behavior in a vertical Taylor–Couette flow. J. Phys.: Conf. Ser. 14, 143–156.Google Scholar
Murai, Y., Oiwa, H. & Takeda, Y. 2008 Frictional drag reduction in bubbly Couette–Taylor flow. Phys. Fluids 20 (3), 034101.Google Scholar
Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A. 2009 Heat transfer mechanisms in bubbly Rayleigh–Bénard convection. Phys. Rev. E 80 (2), 026304.Google ScholarPubMed
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., Van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014a Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26 (1), 015114.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014c Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech. 761, 1–26.Google Scholar
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Pang, M. J., Wei, J. J. & Yu, B. 2014 Numerical study on modulation of microbubbles on turbulence frictional drag in a horizontal channel. Ocean Engng 81, 58–68.Google Scholar
Park, H. J., Tasaka, Y., Oishi, Y. & Murai, Y. 2015 Drag reduction promoted by repetitive bubble injection in turbulent channel flows. Intl J. Multiphase Flow 75, 12–25.CrossRefGoogle Scholar
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R. 2015 A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids 116, 10–16.Google Scholar
Pope, S. B. 2000 Turbulent Flow. Cambridge University Press.Google Scholar
Prosperetti, A. & Tryggvason, G. 2007 Computational Methods for Multiphase Flow. Cambridge University Press.Google Scholar
Shiomi, Y., Kutsuna, H., Akagawa, K. & Ozawa, M. 1993 Two-phase flow in an annulus with a rotating inner cylinder (flow pattern in bubbly flow region). Nucl. Engng Des. 141 (1), 27–34.CrossRefGoogle Scholar
Sugiyama, K., Calzavarini, E. & Lohse, D. 2008 Microbubbly drag reduction in Taylor–Couette flow in the wavy vortex regime. J. Fluid Mech. 608, 21–41.Google Scholar
Tryggvason, G., Dabiri, S., Aboulhasanzadeh, B. & Lu, J. 2013 Multiscale considerations in direct numerical simulations of multiphase flows. Phys. Fluids 25 (3), 031302.Google Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.Google Scholar
Watamura, T., Tasaka, Y. & Murai, Y. 2013 Intensified and attenuated waves in a microbubble Taylor–Couette flow. Phys. Fluids 25 (5), 054107.Google Scholar
Xu, J., Maxey, M. R. & Karniadakis, G. E. 2002 Numerical simulation of turbulent drag reduction using micro-bubbles. J. Fluid Mech. 468, 271–281.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1988 An algorithm for tracking fluid particles in numerical simulations of homogeneous turbulence. J. Comput. Phys. 79 (2), 373–416.Google Scholar
Yoshida, K., Tasaka, Y., Murai, Y. & Takeda, T. 2009 Mode transition in bubbly Taylor–Couette flow measured by PTV. J. Phys.: Conf. Ser. 147 (1), 012013.Google Scholar