Article contents
Local versus volume-integrated turbulence and mixing in breaking internal waves on slopes
Published online by Cambridge University Press: 17 February 2017
Abstract
Using direct numerical simulations (DNS), we explore local and volume-integrated measures of turbulence and mixing in breaking internal waves on slopes. We consider eight breaking wave cases with a range of normalized pycnocline thicknesses 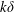 $k\unicode[STIX]{x1D6FF}$ , where
$k\unicode[STIX]{x1D6FF}$ , where 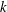 $k$ is the horizontal wavenumber and
$k$ is the horizontal wavenumber and 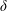 $\unicode[STIX]{x1D6FF}$ is the pycnocline thickness, but with similar incoming wave properties. The energetics of wave breaking is quantified in terms of local turbulent dissipation and irreversible mixing using the method of Scotti & White (J. Fluid Mech., vol. 740, 2014, pp. 114–135). Local turbulent mixing efficiencies are calculated using the irreversible flux Richardson number
$\unicode[STIX]{x1D6FF}$ is the pycnocline thickness, but with similar incoming wave properties. The energetics of wave breaking is quantified in terms of local turbulent dissipation and irreversible mixing using the method of Scotti & White (J. Fluid Mech., vol. 740, 2014, pp. 114–135). Local turbulent mixing efficiencies are calculated using the irreversible flux Richardson number 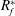 $R_{f}^{\ast }$ and are found to be a function of the turbulent Froude number
$R_{f}^{\ast }$ and are found to be a function of the turbulent Froude number 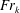 $Fr_{k}$ . Volume-integrated measures of the turbulent mixing efficiency during wave breaking are also made, and are found to be functions of
$Fr_{k}$ . Volume-integrated measures of the turbulent mixing efficiency during wave breaking are also made, and are found to be functions of 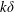 $k\unicode[STIX]{x1D6FF}$ . The bulk turbulent mixing efficiency ranges from 0.25 to 0.37 and is maximized when
$k\unicode[STIX]{x1D6FF}$ . The bulk turbulent mixing efficiency ranges from 0.25 to 0.37 and is maximized when 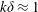 $k\unicode[STIX]{x1D6FF}\approx 1$ . In order to connect local and bulk mixing efficiency measures, the variation in the bulk turbulent mixing efficiency with
$k\unicode[STIX]{x1D6FF}\approx 1$ . In order to connect local and bulk mixing efficiency measures, the variation in the bulk turbulent mixing efficiency with 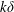 $k\unicode[STIX]{x1D6FF}$ is related to the turbulent Froude number at which the maximum total mixing occurs over the course of the breaking event,
$k\unicode[STIX]{x1D6FF}$ is related to the turbulent Froude number at which the maximum total mixing occurs over the course of the breaking event, 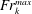 $Fr_{k}^{max}$ . We find that physically,
$Fr_{k}^{max}$ . We find that physically, 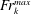 $Fr_{k}^{max}$ is controlled by the vertical length scale of billows at the interface during wave breaking.
$Fr_{k}^{max}$ is controlled by the vertical length scale of billows at the interface during wave breaking.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 16
- Cited by


