Article contents
Scaling laws and flow structures of double diffusive convection in the finger regime
Published online by Cambridge University Press: 08 August 2016
Abstract
Direct numerical simulations are conducted for double diffusive convection (DDC) bounded by two parallel plates. The Prandtl numbers, i.e. the ratios between the viscosity and the molecular diffusivities of scalars, are similar to the values of seawater. The DDC flow is driven by an unstable salinity difference (here across the two plates) and stabilized at the same time by a temperature difference. For these conditions the flow can be in the finger regime. We develop scaling laws for three key response parameters of the system: the non-dimensional salinity flux 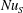 $\mathit{Nu}_{S}$ mainly depends on the salinity Rayleigh number
$\mathit{Nu}_{S}$ mainly depends on the salinity Rayleigh number 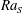 $\mathit{Ra}_{S}$ , which measures the strength of the salinity difference and exhibits a very weak dependence on the density ratio
$\mathit{Ra}_{S}$ , which measures the strength of the salinity difference and exhibits a very weak dependence on the density ratio  $\unicode[STIX]{x1D6EC}$ , which is the ratio of the buoyancy forces induced by two scalar differences. The non-dimensional flow velocity
$\unicode[STIX]{x1D6EC}$ , which is the ratio of the buoyancy forces induced by two scalar differences. The non-dimensional flow velocity 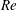 $Re$ and the non-dimensional heat flux
$Re$ and the non-dimensional heat flux 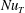 $\mathit{Nu}_{T}$ are dependent on both
$\mathit{Nu}_{T}$ are dependent on both 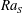 $\mathit{Ra}_{S}$ and
$\mathit{Ra}_{S}$ and 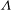 $\unicode[STIX]{x1D6EC}$ . However, the rescaled Reynolds number
$\unicode[STIX]{x1D6EC}$ . However, the rescaled Reynolds number  $Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ and the rescaled convective heat flux
$Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ and the rescaled convective heat flux 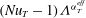 $(\mathit{Nu}_{T}-1)\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{T}^{eff}}$ depend only on
$(\mathit{Nu}_{T}-1)\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{T}^{eff}}$ depend only on 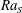 $\mathit{Ra}_{S}$ . The two exponents are dependent on the fluid properties and are determined from the numerical results as
$\mathit{Ra}_{S}$ . The two exponents are dependent on the fluid properties and are determined from the numerical results as  $\unicode[STIX]{x1D6FC}_{u}^{eff}=0.25\pm 0.02$ and
$\unicode[STIX]{x1D6FC}_{u}^{eff}=0.25\pm 0.02$ and  $\unicode[STIX]{x1D6FC}_{T}^{eff}=0.75\pm 0.03$ . Moreover, the behaviours of
$\unicode[STIX]{x1D6FC}_{T}^{eff}=0.75\pm 0.03$ . Moreover, the behaviours of  $\mathit{Nu}_{S}$ and
$\mathit{Nu}_{S}$ and 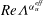 $Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ agree with the predictions of the Grossmann–Lohse theory which was originally developed for the Rayleigh–Bénard flow. The non-dimensional salt-finger width and the thickness of the velocity boundary layers, after being rescaled by
$Re\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}}$ agree with the predictions of the Grossmann–Lohse theory which was originally developed for the Rayleigh–Bénard flow. The non-dimensional salt-finger width and the thickness of the velocity boundary layers, after being rescaled by 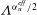 $\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}/2}$ , collapse and obey a similar power-law scaling relation with
$\unicode[STIX]{x1D6EC}^{\unicode[STIX]{x1D6FC}_{u}^{eff}/2}$ , collapse and obey a similar power-law scaling relation with 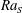 $\mathit{Ra}_{S}$ . When
$\mathit{Ra}_{S}$ . When 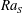 $\mathit{Ra}_{S}$ is large enough, salt fingers do not extend from one plate to the other and horizontal zonal flows emerge in the bulk region. We then show that the current scaling strategy can be successfully applied to the experimental results of a heat–copper–ion system (Hage & Tilgner, Phys. Fluids, vol. 22, 2010, 076603). The fluid has different properties and the exponent
$\mathit{Ra}_{S}$ is large enough, salt fingers do not extend from one plate to the other and horizontal zonal flows emerge in the bulk region. We then show that the current scaling strategy can be successfully applied to the experimental results of a heat–copper–ion system (Hage & Tilgner, Phys. Fluids, vol. 22, 2010, 076603). The fluid has different properties and the exponent 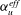 $\unicode[STIX]{x1D6FC}_{u}^{eff}$ takes a different value
$\unicode[STIX]{x1D6FC}_{u}^{eff}$ takes a different value 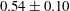 $0.54\pm 0.10$ .
$0.54\pm 0.10$ .
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 37
- Cited by


