Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gandía-Barberá, Sergio
Hoyas, Sergio
Oberlack, Martin
and
Kraheberger, Stefanie
2018.
Letter: The link between the Reynolds shear stress and the large structures of turbulent Couette-Poiseuille flow.
Physics of Fluids,
Vol. 30,
Issue. 4,
Alcántara-Ávila, F.
Hoyas, S.
and
Pérez-Quiles, M.J.
2018.
DNS of thermal channel flow up to Reτ=2000 for medium to low Prandtl numbers.
International Journal of Heat and Mass Transfer,
Vol. 127,
Issue. ,
p.
349.
Lee, Myoungkyu
and
Moser, Robert D.
2019.
Spectral analysis of the budget equation in turbulent channel flows at high Reynolds number.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
886.
Hussain, Zakir
Elazab, Ahmed
Hussain, Sultan
and
Zhang, Huisheng
2019.
Instability of three dimensional electrically conducting fluid of magnetohydrodynamics Couette flow.
AIP Advances,
Vol. 9,
Issue. 10,
Alcántara-Ávila, Francisco
Gandía-Barberá, Sergio
and
Hoyas, Sergio
2019.
Evidences of persisting thermal structures in Couette flows.
International Journal of Heat and Fluid Flow,
Vol. 76,
Issue. ,
p.
287.
Alcántara-Ávila, F.
Gandía-Barberá, S.
and
Hoyas, S.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
225.
Lluesma-Rodríguez, Federico
Álcantara-Ávila, Francisco
Pérez-Quiles, María Jezabel
and
Hoyas, Sergio
2021.
A Code for Simulating Heat Transfer in Turbulent Channel Flow.
Mathematics,
Vol. 9,
Issue. 7,
p.
756.
Yalcin, A.
Turkac, Y.
and
Oberlack, M.
2021.
On the temporal linear stability of the asymptotic suction boundary layer.
Physics of Fluids,
Vol. 33,
Issue. 5,
Bukva, Alexander
Zhang, Kevin
Christopher, Nicholas
and
Hickey, Jean-Pierre
2021.
Assessment of turbulence modeling for massively-cooled turbulent boundary layer flows with transpiration cooling.
Physics of Fluids,
Vol. 33,
Issue. 9,
Monkewitz, Peter A.
2021.
The late start of the mean velocity overlap log law at – a generic feature of turbulent wall layers in ducts.
Journal of Fluid Mechanics,
Vol. 910,
Issue. ,
Aguilar-Fuertes, Jose J.
Noguero-Rodríguez, Francisco
Jaen Ruiz, José C.
García-RAffi, Luis M.
and
Hoyas, Sergio
2021.
Tracking Turbulent Coherent Structures by Means of Neural Networks.
Energies,
Vol. 14,
Issue. 4,
p.
984.
Amo-Navarro, Jesús
Vinuesa, Ricardo
Conejero, J. Alberto
and
Hoyas, Sergio
2021.
Two-Dimensional Compact-Finite-Difference Schemes for Solving the bi-Laplacian Operator with Homogeneous Wall-Normal Derivatives.
Mathematics,
Vol. 9,
Issue. 19,
p.
2508.
Gandía-Barberá, Sergio
Alcántara-Ávila, Francisco
Hoyas, Sergio
and
Avsarkisov, Victor
2021.
Stratification effect on extreme-scale rolls in plane Couette flows.
Physical Review Fluids,
Vol. 6,
Issue. 3,
Schmekel, D.
Alcántara-Ávila, F.
Hoyas, S.
and
Vinuesa, R.
2022.
Predicting Coherent Turbulent Structures via Deep Learning.
Frontiers in Physics,
Vol. 10,
Issue. ,
Hoyas, Sergio
Oberlack, Martin
Alcántara-Ávila, Francisco
Kraheberger, Stefanie V.
and
Laux, Jonathan
2022.
Wall turbulence at high friction Reynolds numbers.
Physical Review Fluids,
Vol. 7,
Issue. 1,
Monkewitz, Peter A.
2022.
Asymptotics of streamwise Reynolds stress in wall turbulence.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Alfwzan, Wafa F.
Hussain, Zakir
Al-Khaled, Kamel
Riaz, Arshad
Abdelhamid, Talaat
Khan, Sami Ullah
Javid, Khurram
Tag El-Din, El Sayed M.
and
Chammam, Wathek
2023.
An optimized stability framework for three-dimensional Hartman flow via Chebyshev collocation simulations.
Results in Physics,
Vol. 49,
Issue. ,
p.
106497.
Dokoza, Toni
Hennings de Lara, Joao Vinicius
and
Oberlack, Martin
2024.
Invariant scaling laws for plane Couette flow with wall-transpiration.
Physics of Fluids,
Vol. 36,
Issue. 3,
Hoyas, Sergio
and
Oberlack, Martin
2024.
Turbulent Couette flow up to.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Nabae, Yusuke
and
Fukagata, Koji
2024.
Theoretical and numerical analyses of turbulent plane Couette flow controlled using uniform blowing and suction.
International Journal of Heat and Fluid Flow,
Vol. 106,
Issue. ,
p.
109286.
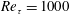 $Re_{\unicode[STIX]{x1D70F}}=1000$
$Re_{\unicode[STIX]{x1D70F}}=1000$ 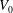 $V_{0}$ , i.e. permeable boundary conditions, such that there is blowing on the lower side and suction on the upper side. Hence, there is no net change in flux to preserve periodic boundary conditions in the streamwise direction. Simulations were performed at
$V_{0}$ , i.e. permeable boundary conditions, such that there is blowing on the lower side and suction on the upper side. Hence, there is no net change in flux to preserve periodic boundary conditions in the streamwise direction. Simulations were performed at 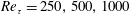 $Re_{\unicode[STIX]{x1D70F}}=250,500,1000$ with varying transpiration rates in the range
$Re_{\unicode[STIX]{x1D70F}}=250,500,1000$ with varying transpiration rates in the range 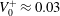 $V_{0}^{+}\approx 0.03$ to 0.085. Additionally, a classical Couette flow case at
$V_{0}^{+}\approx 0.03$ to 0.085. Additionally, a classical Couette flow case at 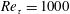 $Re_{\unicode[STIX]{x1D70F}}=1000$ is presented for comparison. As a first key result we found a considerably extended logarithmic region of the mean velocity profile, with constant indicator function
$Re_{\unicode[STIX]{x1D70F}}=1000$ is presented for comparison. As a first key result we found a considerably extended logarithmic region of the mean velocity profile, with constant indicator function 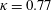 $\unicode[STIX]{x1D705}=0.77$ as transpiration increases. Further, turbulent intensities are observed to decrease with increasing transpiration rate. Mean velocities and intensities collapse only in the cases where the transpiration rate is kept constant, while they are largely insensitive to friction Reynolds number variations. The long and wide characteristic stationary rolls of classical turbulent Couette flow are still present for all present DNS runs. The rolls are affected by wall transpiration, but they are not destroyed even for the largest transpiration velocity case. Spectral information indicates the prevalence of the rolls and the existence of wide structures near the blowing wall. The statistics of all simulations can be downloaded from the webpage of the Chair of Fluid Dynamics.
$\unicode[STIX]{x1D705}=0.77$ as transpiration increases. Further, turbulent intensities are observed to decrease with increasing transpiration rate. Mean velocities and intensities collapse only in the cases where the transpiration rate is kept constant, while they are largely insensitive to friction Reynolds number variations. The long and wide characteristic stationary rolls of classical turbulent Couette flow are still present for all present DNS runs. The rolls are affected by wall transpiration, but they are not destroyed even for the largest transpiration velocity case. Spectral information indicates the prevalence of the rolls and the existence of wide structures near the blowing wall. The statistics of all simulations can be downloaded from the webpage of the Chair of Fluid Dynamics.

