Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lishchuk, Sergey V.
2016.
Dilatational viscosity of dilute particle-laden fluid interface at different contact angles.
Physical Review E,
Vol. 94,
Issue. 6,
Vandadi, Vahid
Jafari Kang, Saeed
and
Masoud, Hassan
2016.
Reciprocal theorem for convective heat and mass transfer from a particle in Stokes and potential flows.
Physical Review Fluids,
Vol. 1,
Issue. 2,
Boniello, Giuseppe
Stocco, Antonio
Gross, Michel
In, Martin
Blanc, Christophe
and
Nobili, Maurizio
2016.
Translational viscous drags of an ellipsoid straddling an interface between two fluids.
Physical Review E,
Vol. 94,
Issue. 1,
Vidal, A.
and
Botto, L.
2017.
Slip flow past a gas–liquid interface with embedded solid particles.
Journal of Fluid Mechanics,
Vol. 813,
Issue. ,
p.
152.
Koplik, Joel
and
Maldarelli, Charles
2017.
Diffusivity and hydrodynamic drag of nanoparticles at a vapor-liquid interface.
Physical Review Fluids,
Vol. 2,
Issue. 2,
Pandey, Anupam
Karpitschka, Stefan
Lubbers, Luuk A.
Weijs, Joost H.
Botto, Lorenzo
Das, Siddhartha
Andreotti, Bruno
and
Snoeijer, Jacco H.
2017.
Dynamical theory of the inverted cheerios effect.
Soft Matter,
Vol. 13,
Issue. 35,
p.
6000.
De Corato, M.
and
Garbin, V.
2018.
Capillary interactions between dynamically forced particles adsorbed at a planar interface and on a bubble.
Journal of Fluid Mechanics,
Vol. 847,
Issue. ,
p.
71.
Das, Subhabrata
Koplik, Joel
Farinato, Raymond
Nagaraj, D. R.
Maldarelli, Charles
and
Somasundaran, Ponisseril
2018.
The Translational and Rotational Dynamics of a Colloid Moving Along the Air-Liquid Interface of a Thin Film.
Scientific Reports,
Vol. 8,
Issue. 1,
Vasudevan, Siddarth A.
Rauh, Astrid
Kröger, Martin
Karg, Matthias
and
Isa, Lucio
2018.
Dynamics and Wetting Behavior of Core–Shell Soft Particles at a Fluid–Fluid Interface.
Langmuir,
Vol. 34,
Issue. 50,
p.
15370.
Huerre, Axel
De Corato, Marco
and
Garbin, Valeria
2018.
Dynamic capillary assembly of colloids at interfaces with 10,000g accelerations.
Nature Communications,
Vol. 9,
Issue. 1,
Gaddam, Anvesh
Agrawal, Amit
Joshi, Suhas S.
and
Thompson, Mark C.
2018.
Slippage on a particle-laden liquid-gas interface in textured microchannels.
Physics of Fluids,
Vol. 30,
Issue. 3,
Pittman, Matthew
and
Chen, Yun
2018.
3D-printed magnetic tweezers for dorsal traction force measurement.
BioTechniques,
Vol. 65,
Issue. 6,
p.
347.
Jiang, Jia-Zong
Zhang, Song
Liu, Lei
and
Sun, Bao-Min
2018.
A microscopic experimental study of nanoparticle motion for the enhancement of oxygen absorption in nanofluids.
Nanotechnology Reviews,
Vol. 7,
Issue. 6,
p.
529.
Planchette, Carole
Lorenceau, Elise
and
Biance, Anne-Laure
2018.
Rupture of granular rafts: effects of particle mobility and polydispersity.
Soft Matter,
Vol. 14,
Issue. 31,
p.
6419.
Song, Dong
Song, Baowei
Hu, Haibao
Du, Xiaosong
Du, Peng
Choi, Chang-Hwan
and
Rothstein, Jonathan P.
2018.
Effect of a surface tension gradient on the slip flow along a superhydrophobic air-water interface.
Physical Review Fluids,
Vol. 3,
Issue. 3,
Cristofolini, Luigi
Orsi, Davide
and
Isa, Lucio
2018.
Characterization of the dynamics of interfaces and of interface-dominated systems via spectroscopy and microscopy techniques.
Current Opinion in Colloid & Interface Science,
Vol. 37,
Issue. ,
p.
13.
Maleki, Amir
and
Frigaard, Ian A.
2018.
Tracking fluid interfaces in primary cementing of surface casing.
Physics of Fluids,
Vol. 30,
Issue. 9,
Grosjean, Galien
Hubert, Maxime
Collard, Ylona
Sukhov, Alexander
Harting, Jens
Smith, Ana-Sunčana
and
Vandewalle, Nicolas
2019.
Capillary assemblies in a rotating magnetic field.
Soft Matter,
Vol. 15,
Issue. 44,
p.
9093.
Terrazas, Ronald
De Maeijer, Adrien
Bolopion, Aude
Gauthier, Michaël
Kinnaert, Michel
and
Lambert, Pierre
2019.
Thermocapillary micromanipulation: force characterization and Cheerios interactions.
Journal of Micro-Bio Robotics,
Vol. 15,
Issue. 1,
p.
13.
Koplik, Joel
and
Maldarelli, Charles
2019.
Molecular dynamics study of the translation and rotation of amphiphilic Janus nanoparticles at a vapor-liquid surface.
Physical Review Fluids,
Vol. 4,
Issue. 4,
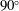 $90^{\circ }$ and
$90^{\circ }$ and 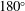 $180^{\circ }$ contact angles. The model agrees well with the experimental and numerical data from the literature. Also, an advantage of the method utilized is that the drag and diffusion coefficients can be calculated up to one order higher in the perturbation parameter than the known velocity and pressure fields. Extensions to other particle shapes with known velocity and pressure fields are straightforward.
$180^{\circ }$ contact angles. The model agrees well with the experimental and numerical data from the literature. Also, an advantage of the method utilized is that the drag and diffusion coefficients can be calculated up to one order higher in the perturbation parameter than the known velocity and pressure fields. Extensions to other particle shapes with known velocity and pressure fields are straightforward.

