Article contents
Drag control in wall-bounded turbulent flows via spanwise opposed wall-jet forcing
Published online by Cambridge University Press: 13 August 2018
Abstract
Drag control using a newly developed spanwise opposed wall-jet forcing (SOJF) method is studied via direct numerical simulation of the incompressible Navier–Stokes equations in a turbulent channel flow (at the friction Reynolds numbers 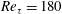 $Re_{\unicode[STIX]{x1D70F}}=180$ and 550). SOJF is characterized by three control parameters: the forcing amplitude
$Re_{\unicode[STIX]{x1D70F}}=180$ and 550). SOJF is characterized by three control parameters: the forcing amplitude 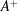 $A^{+}$, the spanwise spacing
$A^{+}$, the spanwise spacing 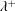 $\unicode[STIX]{x1D706}^{+}$ and the wall-jet height
$\unicode[STIX]{x1D706}^{+}$ and the wall-jet height 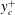 $y_{c}^{+}$ (
$y_{c}^{+}$ (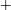 $+$ indicates viscous scaling). At
$+$ indicates viscous scaling). At 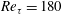 $Re_{\unicode[STIX]{x1D70F}}=180$, notable drag reduction is achieved for wide ranges of
$Re_{\unicode[STIX]{x1D70F}}=180$, notable drag reduction is achieved for wide ranges of 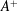 $A^{+}$,
$A^{+}$, 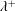 $\unicode[STIX]{x1D706}^{+}$ and
$\unicode[STIX]{x1D706}^{+}$ and 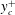 $y_{c}^{+}$, with an optimal drag reduction of approximately 19 % found for
$y_{c}^{+}$, with an optimal drag reduction of approximately 19 % found for 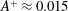 $A^{+}\approx 0.015$,
$A^{+}\approx 0.015$, 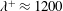 $\unicode[STIX]{x1D706}^{+}\approx 1200$ and
$\unicode[STIX]{x1D706}^{+}\approx 1200$ and 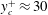 $y_{c}^{+}\approx 30$. The drag reduction results from mergers of numerous low-speed typical individual streaks together by the wall jets, so that the slope of the merged streak envelope and hence the streak strength are reduced below the critical values required for streak instability as well as for transient growth; consequently, the generation of drag inducing near-wall streamwise vortices is suppressed. Through analysis using the FIK identity (Fukagata et al. Phys. Fluids, vol. 14 (11), 2002, pp. L73–L76) in combination with the triple decomposition and the spanwise wavenumber spectrum of the Reynolds shear stress, we find that the control significantly decreases skin friction due to the small scale random turbulent structures (from 75 to 23 % for the optimal case), but injects a dominant contribution at the forcing scale (approximately 34 %). As
$y_{c}^{+}\approx 30$. The drag reduction results from mergers of numerous low-speed typical individual streaks together by the wall jets, so that the slope of the merged streak envelope and hence the streak strength are reduced below the critical values required for streak instability as well as for transient growth; consequently, the generation of drag inducing near-wall streamwise vortices is suppressed. Through analysis using the FIK identity (Fukagata et al. Phys. Fluids, vol. 14 (11), 2002, pp. L73–L76) in combination with the triple decomposition and the spanwise wavenumber spectrum of the Reynolds shear stress, we find that the control significantly decreases skin friction due to the small scale random turbulent structures (from 75 to 23 % for the optimal case), but injects a dominant contribution at the forcing scale (approximately 34 %). As 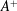 $A^{+}$ or
$A^{+}$ or 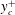 $y_{c}^{+}$ increases, the drag reduction degrades due to the downwash near the initiation of the forcing wall jet. The energy input required for the excitation is found to be small, yielding a 17 % net power saving for the optimal control case. To determine the
$y_{c}^{+}$ increases, the drag reduction degrades due to the downwash near the initiation of the forcing wall jet. The energy input required for the excitation is found to be small, yielding a 17 % net power saving for the optimal control case. To determine the 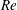 $Re$ dependence of the drag reduction, the control strategy is further validated at a higher
$Re$ dependence of the drag reduction, the control strategy is further validated at a higher 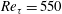 $Re_{\unicode[STIX]{x1D70F}}=550$. If the control parameters are kept the same as at
$Re_{\unicode[STIX]{x1D70F}}=550$. If the control parameters are kept the same as at 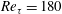 $Re_{\unicode[STIX]{x1D70F}}=180$ (i.e.
$Re_{\unicode[STIX]{x1D70F}}=180$ (i.e. 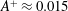 $A^{+}\approx 0.015$,
$A^{+}\approx 0.015$, 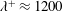 $\unicode[STIX]{x1D706}^{+}\approx 1200$,
$\unicode[STIX]{x1D706}^{+}\approx 1200$, 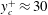 $y_{c}^{+}\approx 30$), the drag reduction decreases to 10 %; however, interestingly, with modestly changed parameters (
$y_{c}^{+}\approx 30$), the drag reduction decreases to 10 %; however, interestingly, with modestly changed parameters (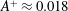 $A^{+}\approx 0.018$,
$A^{+}\approx 0.018$, 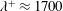 $\unicode[STIX]{x1D706}^{+}\approx 1700$,
$\unicode[STIX]{x1D706}^{+}\approx 1700$, 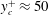 $y_{c}^{+}\approx 50$), drag reduction increases to about 15 %. This additional drag reduction results from the further suppression of turbulent structures in the buffer and log regions. This result, therefore, suggests prospects for drag reduction at even higher
$y_{c}^{+}\approx 50$), drag reduction increases to about 15 %. This additional drag reduction results from the further suppression of turbulent structures in the buffer and log regions. This result, therefore, suggests prospects for drag reduction at even higher 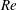 $Re$ via a proper choice of the SOJF parameters.
$Re$ via a proper choice of the SOJF parameters.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 52
- Cited by

