Andereck, C. D., Liu, S. S. & Swinney, H. L.
1986
Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech.
164, 155–183.
Auton, T. R.
1987
The lift force on a spherical body in a rotational flow. J. Fluid Mech.
183, 199–218.
Auton, T. R., Hunt, J. C. R. & Prud’Homme, M.
1988
The force exerted on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech.
197, 241–257.
van den Berg, T. H., van Gils, D. P. M., Lathrop, D. P. & Lohse, D.
2007
Bubbly turbulent drag reduction is a boundary layer effect. Phys. Rev. Lett.
98 (8), 084501.
van den Berg, T. H., Luther, S., Lathrop, D. P. & Lohse, D.
2005
Drag reduction in bubbly Taylor–Couette turbulence. Phys. Rev. Lett.
94 (4), 044501.
Capecelatro, J. & Desjardins, O.
2013
An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys.
238, 1–31.
Ceccio, S. L.
2010
Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech.
42, 183–203.
Chouippe, A., Climent, E., Legendre, D. & Gabillet, C.
2014
Numerical simulation of bubble dispersion in turbulent Taylor–Couette flow. Phys. Fluids
26 (4), 043304.
Climent, E., Simonnet, M. & Magnaudet, J.
2007
Preferential accumulation of bubbles in Couette–Taylor flow patterns. Phys. Fluids
19 (8), 083301.
Dabiri, S., Lu, J. & Tryggvason, G.
2013
Transition between regimes of a vertical channel bubbly upflow due to bubble deformability. Phys. Fluids
25 (10), 102110.
Djeridi, H., Fave, J.-F., Billard, J.-Y. & Fruman, D. H.
1999
Bubble capture and migration in Couette–Taylor flow. Exp. Fluids
26, 233–239.
Djeridi, H., Gabillet, C. & Billard, J. Y.
2004
Two-phase Couette–Taylor flow: arrangement of the dispersed phase and effects on the flow structures. Phys. Fluids
16 (1), 128–139.
Eckhardt, B., Grossmann, S. & Lohse, D.
2007
Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech.
581, 221–250.
Ferrante, A. & Elghobashi, S.
2004
On the physical mechanisms of drag reduction in a spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech.
503, 345–355.
Fokoua, G. N., Gabillet, C., Aubert, A. & Colin, C.
2015
Effect of bubbles arrangement on the viscous torque in bubbly Taylor–Couette flow. Phys. Fluids
27 (3), 034105.
van Gils, D. P. M., Narezo Guzman, D., Sun, C. & Lohse, D.
2013
The importance of bubble deformability for strong drag reduction in bubbly turbulent Taylor–Couette flow. J. Fluid Mech.
722, 317–347.
Grossmann, S., Lohse, D. & Sun, C.
2016
High Reynolds number Taylor–Couette turbulence. Annu. Rev. Fluid Mech.
48 (1), 53–80.
Harleman, M. J. W.2012 On the effect of turbulence on bubbles: experiments and numerical simulations of bubbles in wall-bounded flows. TU Delft, Delft University of Technology.
Jiménez, J.
2011
Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech.
44 (1), 27–45.
Lakkaraju, R., Toschi, F. & Lohse, D.
2014
Bubbling reduces intermittency in turbulent thermal convection. J. Fluid Mech.
745, 1–24.
Lu, J., Fernández, A. & Tryggvason, G.
2005
The effect of bubbles on the wall drag in a turbulent channel flow. Phys. Fluids
17 (9), 095102.
Lu, J. & Tryggvason, G.
2008
Effect of bubble deformability in turbulent bubbly upflow in a vertical channel. Phys. Fluids
20 (4), 040701.
L’vov, V. S., Pomyalov, A., Procaccia, I. & Tiberkevich, V.
2005
Drag reduction by microbubbles in turbulent flows: the limit of minute bubbles. Phys. Rev. Lett.
94 (17), 174502.
Madavan, N. K., Deutsch, S. & Merkle, C. L.1983 Reduction of turbulent skin friction by microbubbles. Tech. Rep. DTIC Document.
Madavan, N. K., Deutsch, S. & Merkle, C. L.
1985
Measurements of local skin friction in a microbubble-modified turbulent boundary layer. J. Fluid Mech.
156, 237–256.
Magnaudet, J. & Eames, I.
2000
The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech.
32 (1), 659–708.
Mazzitelli, I. M., Lohse, D. & Toschi, F.
2003
The effect of microbubbles on developed turbulence. Phys. Fluids
15 (1), L5–L8.
Mei, R. & Klausner, J. F.
1992
Unsteady force on a spherical bubble at finite Reynolds number with small fluctuations in the free-stream velocity. Phys. Fluids.
4 (1), 63–70.
Murai, Y.
2014
Frictional drag reduction by bubble injection. Exp. Fluids
55 (7), 1–28.
Murai, Y., Fukuda, H., Oishi, Y., Kodama, Y. & Yamamoto, F.
2007
Skin friction reduction by large air bubbles in a horizontal channel flow. Intl J. Multiphase Flow
33 (2), 147–163.
Murai, Y., Oiwa, H. & Takeda, Y.
2005
Bubble behavior in a vertical Taylor–Couette flow. J. Phys.: Conf. Ser.
14, 143–156.
Murai, Y., Oiwa, H. & Takeda, Y.
2008
Frictional drag reduction in bubbly Couette–Taylor flow. Phys. Fluids
20 (3), 034101.
Oresta, P., Verzicco, R., Lohse, D. & Prosperetti, A.
2009
Heat transfer mechanisms in bubbly Rayleigh–Bénard convection. Phys. Rev. E
80 (2), 026304.
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., Van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D.
2014a
Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech.
747, 1–29.
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D.
2014b
Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids
26 (1), 015114.
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D.
2014c
Exploring the phase diagram of fully turbulent Taylor–Couette flow. J. Fluid Mech.
761, 1–26.
Ostilla-Mónico, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D.
2013
Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech.
719, 14–46.
Pang, M. J., Wei, J. J. & Yu, B.
2014
Numerical study on modulation of microbubbles on turbulence frictional drag in a horizontal channel. Ocean Engng
81, 58–68.
Park, H. J., Tasaka, Y., Oishi, Y. & Murai, Y.
2015
Drag reduction promoted by repetitive bubble injection in turbulent channel flows. Intl J. Multiphase Flow
75, 12–25.
van der Poel, E. P., Ostilla-Mónico, R., Donners, J. & Verzicco, R.
2015
A pencil distributed finite difference code for strongly turbulent wall-bounded flows. Comput. Fluids
116, 10–16.
Pope, S. B.
2000
Turbulent Flow. Cambridge University Press.
Prosperetti, A. & Tryggvason, G.
2007
Computational Methods for Multiphase Flow. Cambridge University Press.
Shiomi, Y., Kutsuna, H., Akagawa, K. & Ozawa, M.
1993
Two-phase flow in an annulus with a rotating inner cylinder (flow pattern in bubbly flow region). Nucl. Engng Des.
141 (1), 27–34.
Sugiyama, K., Calzavarini, E. & Lohse, D.
2008
Microbubbly drag reduction in Taylor–Couette flow in the wavy vortex regime. J. Fluid Mech.
608, 21–41.
Tryggvason, G., Dabiri, S., Aboulhasanzadeh, B. & Lu, J.
2013
Multiscale considerations in direct numerical simulations of multiphase flows. Phys. Fluids
25 (3), 031302.
Verzicco, R. & Orlandi, P.
1996
A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys.
123 (2), 402–414.
Watamura, T., Tasaka, Y. & Murai, Y.
2013
Intensified and attenuated waves in a microbubble Taylor–Couette flow. Phys. Fluids
25 (5), 054107.
Xu, J., Maxey, M. R. & Karniadakis, G. E.
2002
Numerical simulation of turbulent drag reduction using micro-bubbles. J. Fluid Mech.
468, 271–281.
Yeung, P. K. & Pope, S. B.
1988
An algorithm for tracking fluid particles in numerical simulations of homogeneous turbulence. J. Comput. Phys.
79 (2), 373–416.
Yoshida, K., Tasaka, Y., Murai, Y. & Takeda, T.
2009
Mode transition in bubbly Taylor–Couette flow measured by PTV. J. Phys.: Conf. Ser.
147 (1), 012013.
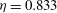${\it\eta}=0.833$
, and a maximum inner cylinder Reynolds number of
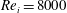$Re_{i}=8000$
is reached. We vary the Froude number (
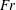$Fr$
), which is the ratio of the centripetal to the gravitational acceleration of the dispersed phase and study its effect on the net torque required to drive the TC system. For the two-phase TC system, we observe drag reduction, i.e. the torque required to drive the inner cylinder is lower compared with that of the single-phase system. The net drag reduction decreases with increasing Reynolds number
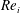$Re_{i}$
, which is consistent with previous experimental findings (Murai et al., J. Phys.: Conf. Ser., vol. 14, 2005, pp. 143–156; Phys. Fluids, vol. 20(3), 2008, 034101). The drag reduction is strongly related to the Froude number: for fixed Reynolds number we observe higher drag reduction when
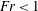$Fr<1$
than for with
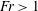$Fr>1$
. This buoyancy effect is more prominent in low
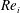$Re_{i}$
systems and decreases with increasing Reynolds number
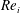$Re_{i}$
. We trace the drag reduction back to the weakening of the angular momentum carrying Taylor rolls by the rising bubbles. We also investigate how the motion of the dispersed phase depends on
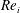$Re_{i}$
and
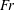$Fr$
, by studying the individual trajectories and mean dispersion of bubbles in the radial and axial directions. Indeed, the less buoyant bubbles (large
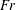$Fr$
) tend to get trapped by the Taylor rolls, while the more buoyant bubbles (small
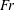$Fr$
) rise through and weaken them.
