1. Introduction
In 1923, Taylor published his ground-breaking experiment and linear stability calculation, whose agreement demonstrated the validity of the Navier–Stokes equations. Since then, Taylor–Couette flow has served as one of the protypical systems in fluid dynamics. In the Taylor–Couette experiment, fluid is confined between two concentric cylinders which rotate at different angular velocities. In laminar Taylor–Couette flow, the motion is purely azimuthal and fluid particles at different radii do not mix. Increasing the angular velocity difference past a critical value leads to the formation of Taylor vortices, toroidal rolls in which circular motion in the meridional
$(r,z)$
plane redistributes fluid and angular momentum between the radii.
Ever since Taylor described and explained the onset of axisymmetric Taylor-vortex flow, an extravagant profusion of three-dimensional patterns of extraordinary variety, beauty and complexity have been discovered experimentally and numerically (e.g. Andereck et al. Reference Andereck, Liu and Swinney1986; Weisshaar et al. Reference Weisshaar, Busse and Nagata1991; Chossat & Iooss Reference Chossat and Iooss1994; Altmeyer et al. Reference Altmeyer, Do, Marques and Lopez2012; Deguchi & Altmeyer Reference Deguchi and Altmeyer2013; Akinaga et al. Reference Akinaga, Generalis and Busse2018). The mathematics of what is called variously equivariant bifurcation theory, symmetry and pattern formation has been brought to bear to predict and explain these spirals and ribbons, twists and waves, modulation and bursts.
Turbulence in Taylor–Couette flow has also been studied, both at high Reynolds number and in the transitional range at low Reynolds number (e.g. Coles Reference Coles1965; Goharzadeh & Mutabazi Reference Goharzadeh and Mutabazi2001; Prigent et al. Reference Prigent, Gregoire, Chaté, Dauchot and van Saarloos2002; Shi et al. Reference Shi, Avila and Hof2013; Lemoult et al. Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016). But who would have thought that there was something new to be learned about turbulence from axisymmetric Taylor–Couette flow?
2. Summary of paper
It has long been known that the Taylor-vortex structure persists even far into the turbulent regime, i.e. that turbulence is superposed on Taylor vortices (e.g. Lathrop et al. Reference Lathrop, Fineberg and Swinney1992; Dong Reference Dong2007; Huisman et al. Reference Huisman, Van Der Veen, Sun and Lohse2014; Grossmann et al. Reference Grossmann, Lohse and Sun2016); long-time averaging accentuates the features of these ghostly vortices. Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) have argued that, under certain hypotheses, transport of angular momentum by chaotic fluctuations in axisymmetric Taylor–Couette flow reproduces the transport associated with the axisymmetric component of turbulent solutions to the full three-dimensional equations. This suggests that the axisymmetric problem could be viewed, not merely as a first step towards turbulence (laminar
$\rightarrow$
axisymmetric Taylor-vortex flow
$\rightarrow$
three-dimensional patterns
$\rightarrow$
turbulence), but as a model for its mean (necessarily axisymmetric) properties. Feldmann & Avila (Reference Feldmann and Avila2025) have carried out long-time axisymmetric simulations of Taylor–Couette flow as a possible route towards studying turbulent structures.
Axisymmetric Taylor-vortex flow consists of an axial stack of toroidal vortices. The vortices are approximately circular, so that the number of vortices is close to the axial-length-to-radial-gap ratio
$\Gamma$
. Feldmann & Avila (Reference Feldmann and Avila2025) observe that the number of vortices remains constant over the course of a simulation. Such a one-dimensional periodic structure is highly constrained and so its possible dynamics are limited: the only remaining possible motion is an axial jiggle or drift of the entire stack of vortices. Feldmann & Avila (Reference Feldmann and Avila2025) find that, for a relatively long system, the rolls carry out diffusive drift (Brownian motion) so that the variance of the phase grows linearly in time. Moreover, the effective diffusion coefficient diverges following a power law as a threshold axial length (or number of rolls)
$\Gamma _c$
is approached from above. For a shorter axial length, although there may be an immediate adjustment of the position, the rolls quickly becomes quasi-stationary, with only weak chaotic motion about a fixed location. For the parameters used by Feldmann & Avila (Reference Feldmann and Avila2025),
$\Gamma _c=10$
; see figure 1. The significance of this sharp threshold is unknown.
Although this is an interesting puzzle by itself, its importance is increased by its generality. Many hydrodynamic systems are driven by an imposed gradient of some quantity. Rolls appear as a means of redistributing this quantity: azimuthal or streamwise velocity for Taylor–Couette, plane Couette or Poiseuille flow, temperature for Rayleigh–Bénard convection, concentration for a binary fluid. Drift has been observed in these other systems (Xi et al. Reference Xi, Zhou and Xia2006; Kreilos et al. Reference Kreilos, Zammert and Eckhardt2014) and according to Feldmann & Avila (Reference Feldmann and Avila2025), the drift appears to be of the same type.
Exploiting the analogy between axisymmetric Taylor–Couette flow and two-dimensional Rayleigh–Bénard convection (Veronis Reference Veronis1970), Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) have proposed a mapping from the two Reynolds numbers (inner and outer, or equivalently, shear
$Re_S$
and rotation
$R_\Omega$
(
$Re_S\equiv Ud/\nu$
and
$R_\Omega\equiv 2d\Omega/U$
where
$d$
is the gap width between the outer and inner cylinders,
$\Omega$
is the angular velocity of the outer cylinder, and
$U$
is the difference between the angular velocities of the inner and outer cylinders times the inner cylinder radius.)) of Taylor–Couette flow (Dubrulle et al. Reference Dubrulle, Dauchot, Daviaud, Longaretti, Richard and Zahn2005) to the single Rayleigh number
$Ra$
of Rayleigh–Bénard convection. Feldmann & Avila (Reference Feldmann and Avila2025) have provided support for this analogy by showing that the diffusion coefficient of the axial drift was the same for different parameter pairs
$(Re_S,R_\Omega )$
yielding the same value of
$Ra$
.
This demonstrates the interest in axisymmetric Taylor–Couette flow from a scientific point of view. However, the imposition of axisymmetry also has the great advantage of economy. Measuring diffusion coefficients of the axial drift requires extremely long times, especially if other parameters are varied as well, i.e. the number of rolls and the Reynolds numbers. Feldmann & Avila (Reference Feldmann and Avila2025) have been able to measure these diffusion coefficients because axisymmetric simulations require only a small fraction of the time that would be required to simulate the three-dimensional flow.
One might associate axial drift (motion of the phase) with axial flux (motion of fluid particles). To investigate this, Feldmann & Avila (Reference Feldmann and Avila2025) have compared simulations in which the axial flux is set to zero with those in which the net axial pressure gradient is zero. Either condition is valid for a periodic direction, but the choice has significant consequences if the flow is not reflection symmetric (e.g. Edwards et al. Reference Edwards, Tagg, Dornblaser, Swinney and Tuckerman1991). Feldmann & Avila (Reference Feldmann and Avila2025) find that in the absence of axial flux, the drift is considerably reduced, but still undergoes Brownian motion.
3. The future
Several questions are raised by this paper. The most obvious and perplexing is the reason for the abrupt threshold. Why are shorter columns tranquil and why are slightly longer columns suddenly so jittery? What physical phenomenon could be responsible for such a sharp distinction?
The second question concerns its generality. Feldmann & Avila (Reference Feldmann and Avila2025) have given convincing evidence that the rolls in other flows, such as Poiseuille flow, Rayleigh–Bénard convection and Taylor–Couette flow with no axial flux, also undergo diffusive drift. Does drift in these flows also have a length threshold? Are the threshold and the power law decay exponent the same?
The third question concerns the applicability of these axisymmetric results to the three-dimensional turbulence which naturally occurs at these high values of Reynolds or Rayleigh number. Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) suggest that some global properties of three-dimensional turbulent Taylor–Couette flow could be captured by its axisymmetric analogue. Is axial drift one of those properties? What other properties might obey this?
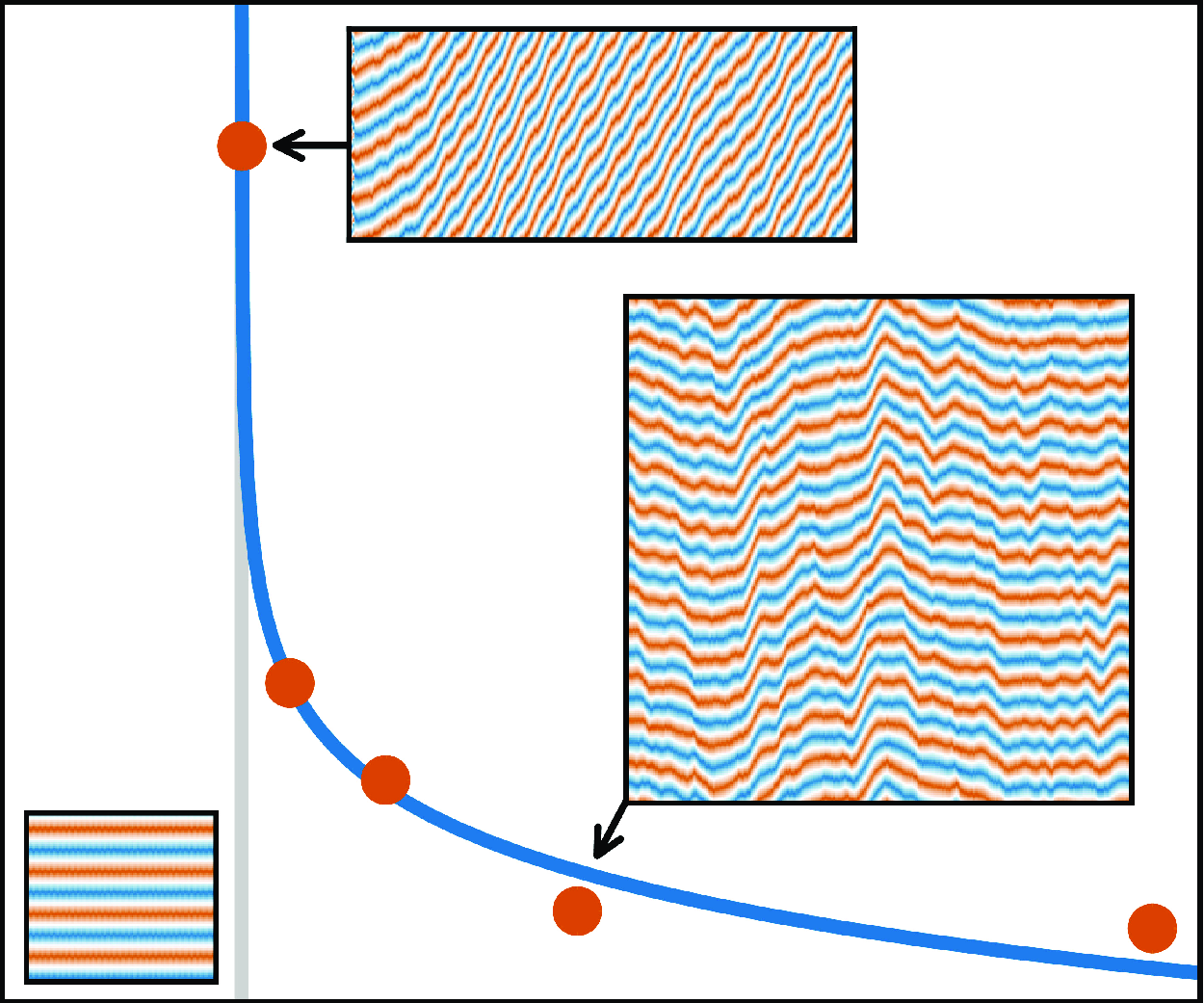
$\Gamma$ of axial length to radial gap corresponds to the number of vortices. For 
$\Gamma =8$, after an initial transient, the vortices do not move, while for 
$\Gamma =10$, they move very quickly in one direction. For 
$\Gamma =12$ and 24, the vortices sporadically change their direction of motion. From Feldmann & Avila (2025).
You have
Access
Open access
1. Introduction
In 1923, Taylor published his ground-breaking experiment and linear stability calculation, whose agreement demonstrated the validity of the Navier–Stokes equations. Since then, Taylor–Couette flow has served as one of the protypical systems in fluid dynamics. In the Taylor–Couette experiment, fluid is confined between two concentric cylinders which rotate at different angular velocities. In laminar Taylor–Couette flow, the motion is purely azimuthal and fluid particles at different radii do not mix. Increasing the angular velocity difference past a critical value leads to the formation of Taylor vortices, toroidal rolls in which circular motion in the meridional
$(r,z)$
plane redistributes fluid and angular momentum between the radii.
Ever since Taylor described and explained the onset of axisymmetric Taylor-vortex flow, an extravagant profusion of three-dimensional patterns of extraordinary variety, beauty and complexity have been discovered experimentally and numerically (e.g. Andereck et al. Reference Andereck, Liu and Swinney1986; Weisshaar et al. Reference Weisshaar, Busse and Nagata1991; Chossat & Iooss Reference Chossat and Iooss1994; Altmeyer et al. Reference Altmeyer, Do, Marques and Lopez2012; Deguchi & Altmeyer Reference Deguchi and Altmeyer2013; Akinaga et al. Reference Akinaga, Generalis and Busse2018). The mathematics of what is called variously equivariant bifurcation theory, symmetry and pattern formation has been brought to bear to predict and explain these spirals and ribbons, twists and waves, modulation and bursts.
Turbulence in Taylor–Couette flow has also been studied, both at high Reynolds number and in the transitional range at low Reynolds number (e.g. Coles Reference Coles1965; Goharzadeh & Mutabazi Reference Goharzadeh and Mutabazi2001; Prigent et al. Reference Prigent, Gregoire, Chaté, Dauchot and van Saarloos2002; Shi et al. Reference Shi, Avila and Hof2013; Lemoult et al. Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016). But who would have thought that there was something new to be learned about turbulence from axisymmetric Taylor–Couette flow?
2. Summary of paper
It has long been known that the Taylor-vortex structure persists even far into the turbulent regime, i.e. that turbulence is superposed on Taylor vortices (e.g. Lathrop et al. Reference Lathrop, Fineberg and Swinney1992; Dong Reference Dong2007; Huisman et al. Reference Huisman, Van Der Veen, Sun and Lohse2014; Grossmann et al. Reference Grossmann, Lohse and Sun2016); long-time averaging accentuates the features of these ghostly vortices. Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) have argued that, under certain hypotheses, transport of angular momentum by chaotic fluctuations in axisymmetric Taylor–Couette flow reproduces the transport associated with the axisymmetric component of turbulent solutions to the full three-dimensional equations. This suggests that the axisymmetric problem could be viewed, not merely as a first step towards turbulence (laminar
$\rightarrow$
axisymmetric Taylor-vortex flow
$\rightarrow$
three-dimensional patterns
$\rightarrow$
turbulence), but as a model for its mean (necessarily axisymmetric) properties. Feldmann & Avila (Reference Feldmann and Avila2025) have carried out long-time axisymmetric simulations of Taylor–Couette flow as a possible route towards studying turbulent structures.
Axisymmetric Taylor-vortex flow consists of an axial stack of toroidal vortices. The vortices are approximately circular, so that the number of vortices is close to the axial-length-to-radial-gap ratio
$\Gamma$
. Feldmann & Avila (Reference Feldmann and Avila2025) observe that the number of vortices remains constant over the course of a simulation. Such a one-dimensional periodic structure is highly constrained and so its possible dynamics are limited: the only remaining possible motion is an axial jiggle or drift of the entire stack of vortices. Feldmann & Avila (Reference Feldmann and Avila2025) find that, for a relatively long system, the rolls carry out diffusive drift (Brownian motion) so that the variance of the phase grows linearly in time. Moreover, the effective diffusion coefficient diverges following a power law as a threshold axial length (or number of rolls)
$\Gamma _c$
is approached from above. For a shorter axial length, although there may be an immediate adjustment of the position, the rolls quickly becomes quasi-stationary, with only weak chaotic motion about a fixed location. For the parameters used by Feldmann & Avila (Reference Feldmann and Avila2025),
$\Gamma _c=10$
; see figure 1. The significance of this sharp threshold is unknown.
Figure 1. Temporal evolution of radial velocity along an axial line at mid-gap. The aspect ratio
$\Gamma$
of axial length to radial gap corresponds to the number of vortices. For
$\Gamma =8$
, after an initial transient, the vortices do not move, while for
$\Gamma =10$
, they move very quickly in one direction. For
$\Gamma =12$
and 24, the vortices sporadically change their direction of motion. From Feldmann & Avila (Reference Feldmann and Avila2025).
Although this is an interesting puzzle by itself, its importance is increased by its generality. Many hydrodynamic systems are driven by an imposed gradient of some quantity. Rolls appear as a means of redistributing this quantity: azimuthal or streamwise velocity for Taylor–Couette, plane Couette or Poiseuille flow, temperature for Rayleigh–Bénard convection, concentration for a binary fluid. Drift has been observed in these other systems (Xi et al. Reference Xi, Zhou and Xia2006; Kreilos et al. Reference Kreilos, Zammert and Eckhardt2014) and according to Feldmann & Avila (Reference Feldmann and Avila2025), the drift appears to be of the same type.
Exploiting the analogy between axisymmetric Taylor–Couette flow and two-dimensional Rayleigh–Bénard convection (Veronis Reference Veronis1970), Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) have proposed a mapping from the two Reynolds numbers (inner and outer, or equivalently, shear
$Re_S$
and rotation
$R_\Omega$
(
$Re_S\equiv Ud/\nu$
and
$R_\Omega\equiv 2d\Omega/U$
where
$d$
is the gap width between the outer and inner cylinders,
$\Omega$
is the angular velocity of the outer cylinder, and
$U$
is the difference between the angular velocities of the inner and outer cylinders times the inner cylinder radius.)) of Taylor–Couette flow (Dubrulle et al. Reference Dubrulle, Dauchot, Daviaud, Longaretti, Richard and Zahn2005) to the single Rayleigh number
$Ra$
of Rayleigh–Bénard convection. Feldmann & Avila (Reference Feldmann and Avila2025) have provided support for this analogy by showing that the diffusion coefficient of the axial drift was the same for different parameter pairs
$(Re_S,R_\Omega )$
yielding the same value of
$Ra$
.
This demonstrates the interest in axisymmetric Taylor–Couette flow from a scientific point of view. However, the imposition of axisymmetry also has the great advantage of economy. Measuring diffusion coefficients of the axial drift requires extremely long times, especially if other parameters are varied as well, i.e. the number of rolls and the Reynolds numbers. Feldmann & Avila (Reference Feldmann and Avila2025) have been able to measure these diffusion coefficients because axisymmetric simulations require only a small fraction of the time that would be required to simulate the three-dimensional flow.
One might associate axial drift (motion of the phase) with axial flux (motion of fluid particles). To investigate this, Feldmann & Avila (Reference Feldmann and Avila2025) have compared simulations in which the axial flux is set to zero with those in which the net axial pressure gradient is zero. Either condition is valid for a periodic direction, but the choice has significant consequences if the flow is not reflection symmetric (e.g. Edwards et al. Reference Edwards, Tagg, Dornblaser, Swinney and Tuckerman1991). Feldmann & Avila (Reference Feldmann and Avila2025) find that in the absence of axial flux, the drift is considerably reduced, but still undergoes Brownian motion.
3. The future
Several questions are raised by this paper. The most obvious and perplexing is the reason for the abrupt threshold. Why are shorter columns tranquil and why are slightly longer columns suddenly so jittery? What physical phenomenon could be responsible for such a sharp distinction?
The second question concerns its generality. Feldmann & Avila (Reference Feldmann and Avila2025) have given convincing evidence that the rolls in other flows, such as Poiseuille flow, Rayleigh–Bénard convection and Taylor–Couette flow with no axial flux, also undergo diffusive drift. Does drift in these flows also have a length threshold? Are the threshold and the power law decay exponent the same?
The third question concerns the applicability of these axisymmetric results to the three-dimensional turbulence which naturally occurs at these high values of Reynolds or Rayleigh number. Eckhardt et al. (Reference Eckhardt, Doering and Whitehead2020) suggest that some global properties of three-dimensional turbulent Taylor–Couette flow could be captured by its axisymmetric analogue. Is axial drift one of those properties? What other properties might obey this?
Declaration of interests
The authors report no conflict of interest.