Article contents
Dynamics of a deformable, transversely rotating droplet released into a uniform flow
Published online by Cambridge University Press: 30 August 2011
Abstract
The effects of transverse rotation on the dynamics of a droplet released into a uniform free stream are numerically investigated. The range of the dimensionless rotation rate is limited to 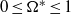 , to avoid any possibility of the droplet breaking up. Droplet dynamics and deformations undergo distinct changes when the dimensionless rotational rate
, to avoid any possibility of the droplet breaking up. Droplet dynamics and deformations undergo distinct changes when the dimensionless rotational rate 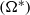 reaches a critical value. The critical rotational rate
reaches a critical value. The critical rotational rate 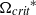 is sensitive to the change in the density ratio, but less dependent on the viscosity ratio and interfacial tension. Below
is sensitive to the change in the density ratio, but less dependent on the viscosity ratio and interfacial tension. Below 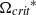 , the droplet drag coefficients are reduced marginally as the effect of the rotation is quickly suppressed by the free stream. Above
, the droplet drag coefficients are reduced marginally as the effect of the rotation is quickly suppressed by the free stream. Above 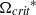 , the drag coefficients decrease initially as the rotation effect dominates at earlier times, resulting in a global minimum. The drag coefficients increase monotonically at later times, when the rotation effects decrease and the free-stream effects become dominant. The only exception is with the increase in the viscosity ratio and the surface tension, which either inhibits droplet deformation or restores the droplet to a more spherical shape in the late stages of droplet evolution. The droplet also experiences lift due to the effects of the transverse rotation. It is observed that the lift coefficients are less dependent on the droplet frontal area as the lift is generated by the velocity difference between the upper and lower interface. In general, the lift coefficients increase with
, the drag coefficients decrease initially as the rotation effect dominates at earlier times, resulting in a global minimum. The drag coefficients increase monotonically at later times, when the rotation effects decrease and the free-stream effects become dominant. The only exception is with the increase in the viscosity ratio and the surface tension, which either inhibits droplet deformation or restores the droplet to a more spherical shape in the late stages of droplet evolution. The droplet also experiences lift due to the effects of the transverse rotation. It is observed that the lift coefficients are less dependent on the droplet frontal area as the lift is generated by the velocity difference between the upper and lower interface. In general, the lift coefficients increase with 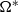 at earlier times and decrease at later times as the difference in the velocity between the upper and lower interface decreases. In some extreme cases, the lift coefficients even become negative.
at earlier times and decrease at later times as the difference in the velocity between the upper and lower interface decreases. In some extreme cases, the lift coefficients even become negative.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 9
- Cited by

