Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-30T17:23:27.167Z Has data issue: false hasContentIssue false
  • English
  • Français

The effect of cell tilting on turbulent thermal convection in a rectangular cell

Published online by Cambridge University Press:  02 December 2014

Shuang-Xi Guo ,
Sheng-Qi Zhou ,
Xian-Rong Cen ,
Ling Qu ,
Yuan-Zheng Lu ,
Liang Sun  and
Xiao-Dong Shang
Shuang-Xi Guo
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China
Sheng-Qi Zhou*
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China
Xian-Rong Cen
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China
Ling Qu
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China
Yuan-Zheng Lu
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China University of Chinese Academy of Sciences, Beijing 100049, PR China
Liang Sun
Affiliation:
School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230022, PR China
Xiao-Dong Shang
Affiliation:
State Key Laboratory of Tropical Oceanography, South China Sea Institute of Oceanology, Chinese Academy of Sciences, Guangzhou 510301, PR China
*
†Email address for correspondence: sqzhou@scsio.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study the influence of cell tilting on flow dynamics and heat transport is explored experimentally within a rectangular cell (aspect ratios 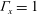${\it\Gamma}_{x}=1$ and 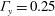${\it\Gamma}_{y}=0.25$ ). The measurements are carried out over a wide range of tilt angles ( 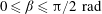$0\leqslant {\it\beta}\leqslant {\rm\pi}/2\ \text{rad}$ ) at a constant Prandtl number ( 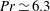$\mathit{Pr}\simeq 6.3$ ) and Rayleigh number ( 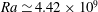$\mathit{Ra}\simeq 4.42\times 10^{9}$ ). The velocity measurements reveal that the large-scale circulation (LSC) is sensitive to the symmetry of the system. In the level case, the high-velocity band of the LSC concentrates at about a quarter of the cell width from the boundary. As the cell is slightly tilted ( 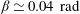${\it\beta}\simeq 0.04\ \text{rad}$ ), the position of the high-velocity band quickly moves towards the boundary. With increasing 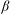${\it\beta}$ , the LSC changes gradually from oblique ellipse-like to square-like, and other more complicated patterns. Oscillations have been found in the temperature and velocity fields for almost all 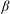${\it\beta}$ , and are strongest at around 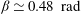${\it\beta}\simeq 0.48\ \text{rad}$ . As 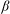${\it\beta}$ increases, the Reynolds number ( 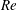$\mathit{Re}$ ) initially also increases, until it reaches its maximum at the transition angle 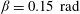${\it\beta}=0.15\ \text{rad}$ , after which it gradually decreases. The cell tilting causes a pronounced reduction of the Nusselt number ( 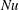$\mathit{Nu}$ ). As 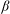${\it\beta}$ increases from 0 to 0.15, 1.05 and 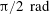${\rm\pi}/2\ \text{rad}$ , the reduction of 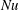$\mathit{Nu}$ is approximately 1.4 %, 5 % and 18 %, respectively. Over the ranges of 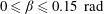$0\leqslant {\it\beta}\leqslant 0.15\ \text{rad}$ , 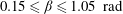$0.15\leqslant {\it\beta}\leqslant 1.05\ \text{rad}$ and 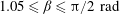$1.05\leqslant {\it\beta}\leqslant {\rm\pi}/2\ \text{rad}$ , the decay slopes are 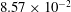$8.57\times 10^{-2}$ , 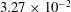$3.27\times 10^{-2}$ and 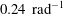$0.24\ \text{rad}^{-1}$ , respectively.

JFM classification

Turbulent Flows: Turbulent convection

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 273 - 287
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G. 2009 Turbulent convection. Physics 2, 74.CrossRefGoogle Scholar
Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–368.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
Ahlers, G. & Xu, X.-C. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.CrossRefGoogle ScholarPubMed
Bairi, A., Laraqi, N. & de María, J. M. G. 2007 Numerical and experimental study of natural convection in tilted parallelepipedic cavities for large Rayleigh numbers. Exp. Therm. Fluid Sci. 31, 309–324.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.CrossRefGoogle ScholarPubMed
Brown, E. & Ahlers, G. 2008 Azimuthal asymmetries of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 20, 105105.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Kadanoff, L., Libchaber, A. & Heslot, F. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.CrossRefGoogle Scholar
Chillà, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Eur. Phys. J. B 40, 223–227.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 1–25.CrossRefGoogle ScholarPubMed
Ciliberto, S., Cioni, S. & Laroche, C. 1996 Large-scale flow properties of turbulent thermal convection. Phys. Rev. E 54, R5901–R5904.CrossRefGoogle ScholarPubMed
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.CrossRefGoogle Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.CrossRefGoogle Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.CrossRefGoogle ScholarPubMed
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54, 34–39.CrossRefGoogle Scholar
Lohse, D. & Xia, K. Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2001 The wind in confined thermal convection. J. Fluid Mech. 449, 169–178.CrossRefGoogle Scholar
Niemela, J. J. & Sreenivasan, K. R. 2003 Rayleigh-number evolution of large-scale coherent motion in turbulent convection. Europhys. Lett. 62, 829–833.CrossRefGoogle Scholar
Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.CrossRefGoogle Scholar
Qiu, X.-L., Shang, X.-D., Tong, P. & Xia, K.-Q. 2004 Velocity oscillations in turbulent Rayleigh–Bénard convection. Phys. Fluids 16, 412–423.CrossRefGoogle Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.CrossRefGoogle ScholarPubMed
Sano, M., Wu, X.-Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.CrossRefGoogle ScholarPubMed
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q. 2003 Measured local heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 90, 074501.CrossRefGoogle ScholarPubMed
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.CrossRefGoogle Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005a Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.CrossRefGoogle Scholar
Villermaux, E. 1995 Memory-induced low frequency oscillations in closed convection boxes. Phys. Rev. Lett. 75, 4618–4621.CrossRefGoogle ScholarPubMed
Wagner, S. & Shishkina, O. 2013 Aspect-ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25, 085110.CrossRefGoogle Scholar
Wei, P. & Xia, K.-Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.CrossRefGoogle Scholar
Weiss, S. & Ahlers, G. 2013 Effect of tilting on turbulent convection: cylindrical samples with aspect ratio ${\it\gamma}=0.5$ . J. Fluid Mech. 715, 314–334.CrossRefGoogle Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.CrossRefGoogle ScholarPubMed
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.CrossRefGoogle ScholarPubMed
Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.CrossRefGoogle ScholarPubMed
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.CrossRefGoogle Scholar
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.CrossRefGoogle Scholar
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007 Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.CrossRefGoogle Scholar