Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-17T19:16:45.450Z Has data issue: false hasContentIssue false
  • English
  • Français

The effects of irregular shape on the particle stress of dilute suspensions

Published online by Cambridge University Press:  02 February 2018

Mohsen Daghooghi  and
Iman Borazjani Open the ORCID record for Iman Borazjani [Opens in a new window]
Mohsen Daghooghi
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, NY 14260, USA
Iman Borazjani*
Affiliation:
Department of Mechanical and Aerospace Engineering, University at Buffalo, State University of New York, Buffalo, NY 14260, USA
*
†Email address for correspondence: iman@tamu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The irregular shape of particles in suspensions is typically approximated by simple geometries such as spheres or ellipsoids. We investigate the accuracy of such an approximation by comparing two irregular-shaped particles with different initial orientations against their equivalent spheroids in dilute volume fractions. Our results show that the average shear particle stress (and also intrinsic viscosity) of irregular particles can be 20 %–120 % higher than the maximum value of their geometric or kinematic equivalent spheroidal particles, and closer to spheroids with higher aspect ratios. We found that two geometric factors of an irregular shape, i.e., dimensionless surface-to-volume ratio and moment of inertia per unit volume (non-dimensionalized by the one-half the largest diameter of the particle), are correlated with the particle stress. In fact, the shear particle stress of a ring-shaped particle, which has a very large value of these factors, is five times larger than its equivalent spheroid. The correlation of these geometric factors with particle stress is further confirmed by considering two families of shapes (cylinder- and sphere-like particles). We also found that acceleration stress and especially Reynolds stress (stress mechanisms due to inertia) can have average values comparable to the stresslet term and effectively increase and decrease the absolute value of the first normal stress difference 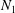$N_{1}$ and second normal stress difference 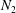$N_{2}$, respectively. However, their contribution to the shear particle stress is negligible. Our results pave the way to define better equivalent particles for irregular ones.

JFM classification

Complex Fluids: Complex Fluids Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 663 - 692
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA.

References

Aidun, C. K. & Clausen, J. R. 2010 Lattice–Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 42, 439–472.CrossRefGoogle Scholar
Aidun, C. K., Lu, Y. & Ding, E.-J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.CrossRefGoogle Scholar
Asgharzadeh, H. & Borazjani, I. 2017 A Newton–Krylov method with an approximate analytical Jacobian for implicit solution of Navier–Stokes equations on staggered overset-curvilinear grids with immersed boundaries. J. Comput. Phys. 331, 227–256.CrossRefGoogle ScholarPubMed
Bagheri, G. H., Bonadonna, C., Manzella, I. & Vonlanthen, P. 2015 On the characterization of size and shape of irregular particles. Powder Technol. 270, 141–153.Google Scholar
Baraff, D. 1997 An introduction to physically based modeling: rigid body simulation I – unconstrained rigid body dynamics. In SIGGRAPH Course Notes, https://www.cs.cmu.edu/∼baraff/sigcourse/notesd2.pdf.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41 (03), 545–570.CrossRefGoogle Scholar
Batchelor, G. K. 1971 The stress generated in a non-dilute suspension of elongated particles by pure straining motion. J. Fluid Mech. 46 (04), 813–829.Google Scholar
Borazjani, I., Ge, L., Le, T. & Sotiropoulos, F. 2013 A parallel overset-curvilinear-immersed boundary framework for simulating complex 3D incompressible flows. Comput. Fluids 77, 76–96.Google Scholar
Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex 3D rigid bodies. J. Comput. Phys. 227 (16), 7587–7620.CrossRefGoogle ScholarPubMed
Bottom, R. G. II, Borazjani, I., Blevins, E. L. & Lauder, G. V. 2016 Hydrodynamics of swimming in stingrays: numerical simulations and the role of the leading-edge vortex. J. Fluid Mech. 788, 407–443.CrossRefGoogle Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1 (2), 195–341.Google Scholar
Bretherton, F. P. 1962 The motion of rigid particles in a shear flow at low Reynolds number. J. Fluid Mech. 14 (02), 284–304.CrossRefGoogle Scholar
Bullard, J. W. & Garboczi, E. J. 2013 Defining shape measures for 3D star-shaped particles: sphericity, roundness and dimensions. Powder Technol. 249, 241–252.Google Scholar
Burgers, J. M. 1995 On the Motion of Small Particles of Elongated Form. Suspended in a Viscous Liquid. Springer.CrossRefGoogle Scholar
Carrasco, B. & de la Torre, J. G. 1999 Hydrodynamic properties of rigid particles: comparison of different modeling and computational procedures. Biophys. J. 76 (6), 3044–3057.Google Scholar
Chaouche, M. & Koch, D. L. 2001 Rheology of non-Brownian rigid fiber suspensions with adhesive contacts. J. Rheol. 45 (2), 369–382.CrossRefGoogle Scholar
Chinesta, F. & Ausias, G. 2015 Rheology of Non-spherical Particle Suspensions. Elsevier.Google Scholar
Chung, S. T. & Kwon, T. H. 1996 Coupled analysis of injection molding filling and fiber orientation, including in-plane velocity gradient effect. Polym. Compos. 17 (6), 859–872.Google Scholar
Claeys, I. L. & Brady, J. F. 1993 Suspensions of prolate spheroids in Stokes flow. Part 1. Dynamics of a finite number of particles in an unbounded fluid. J. Fluid Mech. 251, 411–442.Google Scholar
Cox, R. G. 1971 The motion of long slender bodies in a viscous fluid. Part 2. Shear flow. J. Fluid Mech. 45 (04), 625–657.Google Scholar
Dabade, V., Marath, N. K. & Subramanian, G. 2016 The effect of inertia on the orientation dynamics of anisotropic particles in simple shear flow. J. Fluid Mech. 791, 631–703.Google Scholar
Daghooghi, M. & Borazjani, I. 2015a The hydrodynamic advantages of synchronized swimming in a rectangular pattern. Bioinspir. Biomim. 10 (5), 056018.Google Scholar
Daghooghi, M. & Borazjani, I. 2015b The influence of inertia on the rheology of a periodic suspension of neutrally buoyant rigid ellipsoids. J. Fluid Mech. 781, 506–549.Google Scholar
Daghooghi, M. & Borazjani, I. 2016 Self-propelled swimming simulations of bio-inspired smart structures. Bioinspir. Biomim. 11 (5), 056001.Google Scholar
Daghooghi, M. & Borazjani, I. 2017 The effect of undulations on the particle stress in dilute suspensions of rod-like particles. Eur. J. Comput. Mech. 26 (1–2), 61–77.Google Scholar
Denn, M. M. & Morris, J. F. 2014 Rheology of non-Brownian suspensions. Annu. Rev. Chem. Biomol. Engng 5, 203–228.Google Scholar
Dinh, S. M. & Armstrong, R. C. 1984 A rheological equation of state for semiconcentrated fiber suspensions. J. Rheol. 28 (3), 207–227.Google Scholar
Einarsson, J., Candelier, F., Lundell, F., Angilella, J. R. & Mehlig, B. 2015 Rotation of a spheroid in a simple shear at small Reynolds number. Phys. Fluids 27 (6), 063301.CrossRefGoogle Scholar
Einstein, A. 1956 Investigations on the Theory of the Brownian Movement. Courier Dover Publications.Google Scholar
Eyssautier, J., Frot, D. & Barré, L. 2012 Structure and dynamic properties of colloidal asphaltene aggregates. Langmuir 28 (33), 11997–12004.Google Scholar
Feng, J. & Joseph, D. D. 1995 The unsteady motion of solid bodies in creeping flows. J. Fluid Mech. 303, 83–102.CrossRefGoogle Scholar
Ge, L. & Sotiropoulos, F. 2007 A numerical method for solving the 3D unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 225 (2), 1782–1809.Google Scholar
Ghanavati, M., Shojaei, M.-J. & Ahmad Ramazani, S. A. 2013 Effects of asphaltene content and temperature on viscosity of Iranian heavy crude oil: experimental and modeling study. Energy Fuels 27 (12), 7217–7232.CrossRefGoogle Scholar
Gilmanov, A. & Sotiropoulos, F. 2005 A hybrid Cartesian/immersed boundary method for simulating flows with 3D, geometrically complex, moving bodies. J. Comput. Phys. 207 (2), 457–492.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, vol. 45. Cambridge University Press.Google Scholar
Haddadi, H. & Morris, J. F. 2014 Microstructure and rheology of finite inertia neutrally buoyant suspensions. J. Fluid Mech. 749, 431–459.Google Scholar
Harris, J. B. & Pittman, J. F. T. 1975 Equivalent ellipsoidal axis ratios of slender rod-like particles. J. Colloid Interface Sci. 50 (2), 280–282.Google Scholar
Hedayat, M., Asgharzadeh, H. & Borazjani, I. 2017 Platelet activation of mechanical versus bioprosthetic heart valves during systole. J. Biomech. 56, 111–116.Google Scholar
Hinch, E. J. & Leal, L. G. 1979 Rotation of small non-axisymmetric particles in a simple shear flow. J. Fluid Mech. 92 (03), 591–607.Google Scholar
Huang, H., Wu, Y. & Lu, X. 2012a Shear viscosity of dilute suspensions of ellipsoidal particles with a lattice Boltzmann method. Phys. Rev. E 86 (4), 046305.Google Scholar
Huang, H., Yang, X., Krafczyk, M. & Lu, X.-Y. 2012b Rotation of spheroidal particles in Couette flows. J. Fluid Mech. 692, 369–394.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Jeffrey, D. J. & Acrivos, A. 1976 The rheological properties of suspensions of rigid particles. AIChE J. 22 (3), 417–432.Google Scholar
Karnis, A., Goldsmith, H. L. & Mason, S. G. 1963 Axial migration of particles in poiseuille flow. Nature 200, 159–160.Google Scholar
Karnis, A., Goldsmith, H. L. & Mason, S. G. 1966 The flow of suspensions through tubes: V. Inertial effects. Can. J. Chem. Engng 44 (4), 181–193.Google Scholar
Karrila, S. J., Fuentes, Y. O. & Kim, S. 1989 Parallel computational strategies for hydrodynamic interactions between rigid particles of arbitrary shape in a viscous fluid. J. Rheol. 33 (6), 913–947.CrossRefGoogle Scholar
Ku, X. K. & Lin, J. Z. 2009 Inertial effects on the rotational motion of a fibre in simple shear flow between two bounding walls. Phys. Scr. 80 (2), 025801.CrossRefGoogle Scholar
Kulkarni, P. M. & Morris, J. F. 2008 Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20 (4), 040602.Google Scholar
Kumar, A. & Higdon, J. J. L. 2011a Particle mesh Ewald Stokesian dynamics simulations for suspensions of non-spherical particles. J. Fluid Mech. 675, 297–335.Google Scholar
Kumar, A. & Higdon, J. J. L. 2011b Dynamics of the orientation behavior and its connection with rheology in sheared non-Brownian suspensions of anisotropic dicolloidal particles. J. Rheol. 55 (3), 581–626.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46 (04), 685–703.Google Scholar
Lindström, S. B. & Uesaka, T. 2009 A numerical investigation of the rheology of sheared fiber suspensions. Phys. Fluids 21 (8), 083301.Google Scholar
Lundell, F. 2011 The effect of particle inertia on triaxial ellipsoids in creeping shear: from drift toward chaos to a single periodic solution. Phys. Fluids 23 (1), 011704.Google Scholar
Mader, H. M., Llewellin, E. W. & Mueller, S. P. 2013 The rheology of two-phase magmas: a review and analysis. J. Volcanol. Geotherm. Res. 257, 135–158.Google Scholar
Mao, W. & Alexeev, A. 2014 Motion of spheroid particles in shear flow with inertia. J. Fluid Mech. 749, 145–166.CrossRefGoogle Scholar
Martys, N. S. 2005 Study of a dissipative particle dynamics based approach for modeling suspensions. J. Rheol 49 (2), 401–424.Google Scholar
Mason, S. G. & Manley, R. St. J. 1956 Particle motions in sheared suspensions: orientations and interactions of rigid rods. Proc. R. Soc. Lond. A. 238 (1212), 117–131.Google Scholar
Mikulencak, D. R. & Morris, J. F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.Google Scholar
Mueller, S., Llewellin, E. W. & Mader, H. M. 2010 The rheology of suspensions of solid particles. Proc. R. Soc. Lond. A 466 (2116), 1201–1228.Google Scholar
Mullins, O. C., Sheu, E. Y., Hammami, A. & Marshall, A. G. 2007 Asphaltenes, Heavy Oils, and Petroleomics. Springer Science, Business Media.Google Scholar
Nawab, M. A. & Mason, S. G. 1958 Viscosity of dilute suspensions of thread-like particles. J. Phys. Chem. 62 (10), 1248–1253.Google Scholar
Pabst, W., Gregorová, E. & Berthold, C. 2006 Particle shape and suspension rheology of short-fiber systems. J. Eur. Ceram. Soc. 26 (1), 149–160.Google Scholar
Pal, R. 2015 A new model for the viscosity of asphaltene solutions. Can. J. Chem. Engng 93 (4), 747–755.Google Scholar
Panton, R. L. 1996 Incompressible Flow, 2nd edn. Wiley.Google Scholar
Petrie, C. J. 1999 The rheology of fibre suspensions. J. Non-Newtonian Fluid Mech. 87 (2), 369–402.Google Scholar
Qi, D. & Luo, L.-S. 2003 Rotational and orientational behaviour of three-dimensional spheroidal particles in Couette flows. J. Fluid Mech. 477, 201–213.Google Scholar
Rallison, J. M. 1978 The effects of Brownian rotations in a dilute suspension of rigid particles of arbitrary shape. J. Fluid Mech. 84 (02), 237–263.Google Scholar
Robertson, C. R. & Acrivos, A. 1970 Low Reynolds number shear flow past a rotating circular cylinder. Part 1. Momentum transfer. J. Fluid Mech. 40 (04), 685–703.Google Scholar
Rosén, T., Do-Quang, M., Aidun, C. K. & Lundell, F. 2015a The dynamical states of a prolate spheroidal particle suspended in shear flow as a consequence of particle and fluid inertia. J. Fluid Mech. 771, 115–158.Google Scholar
Rosén, T., Do-Quang, M., Aidun, C. K. & Lundell, F. 2015b Effect of fluid and particle inertia on the rotation of an oblate spheroidal particle suspended in linear shear flow. Phys. Rev. E 91 (5), 053017.Google Scholar
Rosén, T., Einarsson, J., Nordmark, A., Aidun, C. K., Lundell, F. & Mehlig, B. 2015c Numerical analysis of the angular motion of a neutrally buoyant spheroid in shear flow at small Reynolds numbers. Phys. Rev. E 92 (6), 063022.Google Scholar
Rosén, T., Lundell, F. & Aidun, C. K. 2014 Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. J. Fluid Mech. 738, 563–590.CrossRefGoogle Scholar
Rubio-Hernández, F. J., Ayucar-Rubio, M. F., Velazquez-Navarro, J. F. & Galindo-Rosales, F. J. 2006 Intrinsic viscosity of SiO2 , Al2 O3 and TiO2 aqueous suspensions. J. Colloid Interface Sci. 298 (2), 967–972.Google Scholar
Shaqfeh, E. S. & Fredrickson, G. H. 1990 The hydrodynamic stress in a suspension of rods. Phys. Fluids A 2 (1), 7–24.Google Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.Google Scholar
Subramanian, G. & Koch, D. L. 2006 Inertial effects on the orientation of nearly spherical particles in simple shear flow. J. Fluid Mech. 557, 257–296.Google Scholar
Subramanian, G., Koch, D. L., Zhang, J. & Yang, C. 2011 The influence of the inertially dominated outer region on the rheology of a dilute dispersion of low-Reynolds-number drops or rigid particles. J. Fluid Mech. 674, 307–358.CrossRefGoogle Scholar
Taylor, M. A., Garboczi, E. J., Erdogan, S. T. & Fowler, D. W. 2006 Some properties of irregular 3-d particles. Powder Technol. 162 (1), 1–15.CrossRefGoogle Scholar
Yang, S.-M., Kim, S.-H., Lim, J.-M. & Yi, G.-R. 2008 Synthesis and assembly of structured colloidal particles. J. Mater. Chem. 18 (19), 2177–2190.Google Scholar
Yarin, A. L., Gottlieb, O. & Roisman, I. V. 1997 Chaotic rotation of triaxial ellipsoids in simple shear flow. J. Fluid Mech. 340, 83–100.Google Scholar
Yeo, K. & Maxey, M. R. 2013 Dynamics and rheology of concentrated, finite-Reynolds-number suspensions in a homogeneous shear flow. Phys. Fluids 25 (5), 053303.Google Scholar
Youngren, G. K. & Acrivos, A. 1975 Stokes flow past a particle of arbitrary shape: a numerical method of solution. J. Fluid Mech. 69 (02), 377–403.Google Scholar
Yu, Z., Phan-Thien, N. & Tanner, R. I. 2007 Rotation of a spheroid in a Couette flow at moderate Reynolds numbers. Phys. Rev. E 76 (2), 026310.Google Scholar

Daghooghi and Borazjani supplemenatary movie 1

The motion of particles for case 1 (left), 2 (middle), and 3 (right). In case 1 and 2 a Kayaking motion is observed while in case 3 the particle motion is almost planar.

Download Daghooghi and Borazjani supplemenatary movie 1(Video)
Video 27.7 MB