Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-24T05:35:10.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Electroosmosis over non-uniformly charged surfaces: modified Smoluchowski slip velocity for second-order fluids

Published online by Cambridge University Press:  15 November 2016

Uddipta Ghosh ,
Kaustav Chaudhury  and
Suman Chakraborty
Uddipta Ghosh
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur 721302, West Bengal, India
Kaustav Chaudhury
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur 721302, West Bengal, India
Suman Chakraborty*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur 721302, West Bengal, India
*
†Email address for correspondence: suman@mech.iitkgp.ernet.in
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper we focus on deriving the modified Smoluchowski slip velocity of second-order fluids, for electroosmotic flows over plane surfaces with arbitrary non-uniform surface potential in the presence of thin electric double layers (EDLs). 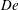We employ matched asymptotic expansion to stretch the electric double layer and subsequently apply regular asymptotic expansions taking the Deborah number ($De$) as the gauge function. Modified slip velocities correct up to 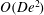$O(De^{2})$ are presented. Two sample cases are considered to demonstrate the effects of viscoelasticity on slip velocity: (i) an axially periodic patterned potential and (ii) a step-change-like variation in the surface potential. The central result of our analysis is that, unlike Newtonian fluids, the electroosmotic slip velocity for second-order fluids does not, in general, align with the direction of the applied external electric field. Proceeding further forward, we show that the slip velocity in a given direction may, in fact, depend on the applied electric field strength in a mutually orthogonal direction, considering three dimensionality of the flow structure. In addition, we demonstrate that the modified slip velocity is not proportional to the zeta potential, as in the cases of Newtonian fluids; rather it depends strongly on the gradients of the interfacial potential as well. Our results are likely to have potential implications so far as the design of charge modulated microfluidic devices transporting rheologically complex fluids is concerned, such as for mixing and bio-reactive system analysis in lab-on-a-chip-based micro-total-analysis systems handling bio-fluids.

JFM classification

Micro-/Nano-fluid dynamics: Microfluidics Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 809 , 25 December 2016 , pp. 664 - 690
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afonso, A. M., Alves, M. A. & Pinho, F. T. 2009 Analytical solution of mixed electro-osmotic/pressure driven flows of viscoelastic fluids in microchannels. J. Non-Newtonian Fluid Mech. 159 (1–3), 50–63.Google Scholar
Afonso, A. M., Alves, M. A. & Pinho, F. T. 2010 Electro-osmotic flow of viscoelastic fluids in microchannels under asymmetric zeta potentials. J. Engng Maths 71 (1), 15–30.Google Scholar
Afonso, A. M., Alves, M. A. & Pinho, F. T. 2013 Analytical solution of two-fluid electro-osmotic flows of viscoelastic fluids. J. Colloid Interface Sci. 395, 277–286.Google Scholar
Ajdari, A. 1995 Electro-osmosis on inhomogeneously charged surfaces. Phys. Rev. Lett. 75 (4), 755–758.CrossRefGoogle ScholarPubMed
Ajdari, A. 1996 Generation of transverse fluid currents and forces by an electric field: electro-osmosis on charge-modulated and undulated surfaces. Phys. Rev. E 53 (5), 4996–5005.Google Scholar
Ajdari, A. 2001 Transverse electrokinetic and microfluidic effects in micropatterned channels: lubrication analysis for slab geometries. Phys. Rev. E 65 (1), 1–9.Google ScholarPubMed
Ardekani, A. M., Joseph, D. D., Dunn-Rankin, D. & Rangel, R. H. 2009 Particle-wall collision in a viscoelastic fluid. J. Fluid Mech. 633, 475–483.Google Scholar
Bahga, S. S., Vinogradova, O. I. & Bazant, M. Z. 2010 Anisotropic electro-osmotic flow over super-hydrophobic surfaces. J. Fluid Mech. 644, 245–255.Google Scholar
Bandopadhyay, A. & Chakraborty, S. 2012 Giant augmentations in electro-hydro-dynamic energy conversion efficiencies of nanofluidic devices using viscoelastic fluids. Appl. Phys. Lett. 101 (4), 043905.Google Scholar
Bandopadhyay, A., Ghosh, U. & Chakraborty, S. 2013 Time periodic electroosmosis of linear viscoelastic liquids over patterned charged surfaces in microfluidic channels. J. Non-Newtonian Fluid Mech. 202, 1–11.Google Scholar
Bazant, M., Thornton, K. & Ajdari, A. 2004 Diffuse-charge dynamics in electrochemical systems. Phys. Rev. E 70 (2), 021506.Google ScholarPubMed
Belyaev, A. V. & Vinogradova, O. I. 2010 Effective slip in pressure-driven flow past super-hydrophobic stripes. J. Fluid Mech. 652, 489–499.Google Scholar
Belyaev, A. V. & Vinogradova, O. I. 2011 Electro-osmosis on anisotropic superhydrophobic surfaces. Phys. Rev. Lett. 107 (9), 098301.Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers I. Springer.Google Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Volume 1: Fluid Mechanics. Wiley.Google Scholar
Brotherton, C. M. & Davis, R. H. 2004 Electroosmotic flow in channels with step changes in zeta potential and cross section. J. Colloid Interface Sci. 270 (1), 242–246.Google Scholar
Brunet, E. & Ajdari, A. 2006 Thin double layer approximation to describe streaming current fields in complex geometries: analytical framework and applications to microfluidics. Phys. Rev. E 73 (5), 056306.Google Scholar
Brust, M. et al. 2013 Rheology of human blood plasma: viscoelastic versus Newtonian behavior. Phys. Rev. Lett. 110 (7), 078305.Google Scholar
Chan, P. C.-H. & Leal, L. G. 1979 The motion of a deformable drop in a second-order fluid. J. Fluid Mech. 92 (01), 131–170.CrossRefGoogle Scholar
Chang, C.-C. & Yang, R.-J. 2008 Chaotic mixing in a microchannel utilizing periodically switching electro-osmotic recirculating rolls. Phys. Rev. E 77 (5), 056311.Google Scholar
Chaudhury, K., Ghosh, U. & Chakraborty, S. 2013 Substrate wettability induced alterations in convective heat transfer characteristics in microchannel flows: an order parameter approach. Intl J. Heat Mass Transfer 67, 1083–1095.CrossRefGoogle Scholar
Chen, C.-K. & Cho, C.-C. 2008 A combined active/passive scheme for enhancing the mixing efficiency of microfluidic devices. Chem. Engng Sci. 63 (12), 3081–3087.Google Scholar
Das, S. & Chakraborty, S. 2006 Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 559 (1), 15–24.Google Scholar
Dhar, J., Bandopadhyay, A. & Chakraborty, S. 2013 Electro-osmosis of electrorheological fluids. Phys. Rev. E 88 (5), 053001.Google Scholar
Dhar, J., Ghosh, U. & Chakraborty, S. 2014 Alterations in streaming potential in presence of time periodic pressure-driven flow of a power law fluid in narrow confinements with nonelectrostatic ion–ion interactions. Electrophoresis 35 (5), 662–669.Google Scholar
Dukhin, S. S. 1993 Non-equilibrium electric surface phenomena. Adv. Colloid Interface Sci. 44, 1–134.Google Scholar
Ferrás, L. L. et al. 2014 Analytical and numerical study of the electro-osmotic annular flow of viscoelastic fluids. J. Colloid Interface Sci. 420, 152–157.Google Scholar
Feuillebois, F., Bazant, M. Z. & Vinogradova, O. I. 2010 Transverse flow in thin superhydrophobic channels. Phys. Rev. E 82 (5), 055301.Google Scholar
Fu, L. 2003 Analysis of electroosmotic flow with step change in zeta potential. J. Colloid Interface Sci. 258 (2), 266–275.Google Scholar
Ghosal, S. 2002 Lubrication theory for electro-osmotic flow in a microfluidic channel of slowly varying cross-section and wall charge. J. Fluid Mech. 459, 103–128.CrossRefGoogle Scholar
Ghosh, U. & Chakraborty, S. 2013 Electrokinetics over charge-modulated surfaces in the presence of patterned wettability: role of the anisotropic streaming potential. Phys. Rev. E 88 (3), 033001.Google ScholarPubMed
Ghosh, U. & Chakraborty, S. 2015 Electroosmosis of viscoelastic fluids over charge modulated surfaces in narrow confinements. Phys. Fluids 27 (6), 062004.Google Scholar
Green, N. G. et al. 2002 Fluid flow induced by nonuniform AC electric fields in electrolytes on microelectrodes. III: observation of streamlines and numerical simulation. Phys. Rev. E 66 (2), 026305.Google Scholar
Griffiths, D. F., Jones, D. T. & Walters, K. 1969 A flow reversal due to edge effects. J. Fluid Mech. 36 (01), 161–175.Google Scholar
Højgaard Olesen, L., Bazant, M. Z. & Bruus, H. 2010 Strongly nonlinear dynamics of electrolytes in large AC voltages. Phys. Rev. E 82 (1), 011501.Google Scholar
Hunter, R. J. 1981 Zeta Potential in Colloid Science: Principles and Applications. Academic.Google Scholar
Jacqmin, D. 1999 Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 127, 96–127.Google Scholar
Joseph, D. & Feng, J. 1996 A note on the forces that move particles in a second-order fluid. J. Non-Newtonian Fluid Mech. 64, 299–302.Google Scholar
Khair, A. S. & Squires, T. M. 2008 Fundamental aspects of concentration polarization arising from nonuniform electrokinetic transport. Phys. Fluids 20 (8), 087102.Google Scholar
Kundu, P. K. & Cohen, I. M. 2004 Fluid Mechanics. Elsevier Academic.Google Scholar
Leal, L. G. 1975 The slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 69 (02), 305–337.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena. Cambridge University Press.Google Scholar
Li, F. et al. 2007 Linear stability of a two-fluid interface for electrohydrodynamic mixing in a channel. J. Fluid Mech. 583, 347–377.Google Scholar
Mandal, S., Ghosh, U., Bandopadhyay, A. & Chakraborty, S. 2015 Electro-osmosis of superimposed fluids in the presence of modulated charged surfaces in narrow confinements. J. Fluid Mech. 776, 390–429.CrossRefGoogle Scholar
Mortensen, N. et al. 2005 Electrohydrodynamics of binary electrolytes driven by modulated surface potentials. Phys. Rev. E 71 (5), 056306.Google Scholar
Nayfeh, A. H. 2011 An Introduction to Perturbation Methods. Wiley.Google Scholar
Ng, C.-O. & Chu, H. C. W. 2011 Electrokinetic flows through a parallel-plate channel with slipping stripes on walls. Phys. Fluids 23 (10), 102002.Google Scholar
Ng, C.-O. & Qi, C. 2014 Electroosmotic flow of a power-law fluid in a non-uniform microchannel. J. Non-Newtonian Fluid Mech. 208–209, 118–125.Google Scholar
Nguyen, T. et al. 2013 Highly enhanced energy conversion from the streaming current by polymer addition. Lab on a Chip 13 (16), 3210–3216.Google Scholar
Norouzi, M. et al. 2010 Flow of second-order fluid in a curved duct with square cross-section. J. Non-Newtonian Fluid Mech. 165 (7–8), 323–339.Google Scholar
Ohshima, H. 2006 Theory of Colloid and Interfacial Electric Phenomena. Elsevier.Google Scholar
Ou, J., Moss, G. R. & Rothstein, J. P. 2007 Enhanced mixing in laminar flows using ultrahydrophobic surfaces. Phys. Rev. E 76 (1), 016304.Google Scholar
Patankar, S. 1980 Numerical Hear Transfer and Fluid Flow. CRC Press.Google Scholar
Qi, C. & Ng, C.-O. 2015a Electroosmotic flow of a power-law fluid in a slit microchannel with gradually varying channel height and wall potential. Eur. J. Mech. (B/Fluids) 52, 160–168.Google Scholar
Qi, C. & Ng, C.-O. 2015b Electroosmotic flow of a power-law fluid through an asymmetrical slit microchannel with gradually varying wall shape and wall potential. Colloids Surf. A 472, 26–37.Google Scholar
Rubinstein, I. & Zaltzman, B. 2001 Electro-osmotic slip of the second kind and instability in concentration polarization at electrodialysis membranes. Math. Models Meth. Appl. Sci. 11 (02), 263–300.Google Scholar
Rubinstein, I., Zaltzman, B. & Lerman, I. 2005 Electroconvective instability in concentration polarization and nonequilibrium electro-osmotic slip. Phys. Rev. E 72 (1), 011505.Google ScholarPubMed
Saprykin, S., Koopmans, R. J. & Kalliadasis, S. 2007 Free-surface thin-film flows over topography: influence of inertia and viscoelasticity. J. Fluid Mech. 578, 271–293.Google Scholar
Saville, D. A. 1977 Electrokinetic effects with small particles. Annu. Rev. Fluid Mech. 9 (1), 321–337.Google Scholar
Schmieschek, S. et al. 2012 Tensorial slip of superhydrophobic channels. Phys. Rev. E 85 (1), 016324.Google Scholar
Schnitzer, O. & Yariv, E. 2012a Induced-charge electro-osmosis beyond weak fields. Phys. Rev. E 86 (6), 061506.Google Scholar
Schnitzer, O. & Yariv, E. 2012b Macroscale description of electrokinetic flows at large zeta potentials: nonlinear surface conduction. Phys. Rev. E 86 (2), 021503.Google Scholar
Schnitzer, O. & Yariv, E. 2012c Strong-field electrophoresis. J. Fluid Mech. 701, 333–351.Google Scholar
Schnitzer, O. & Yariv, E. 2014 Strong electro-osmotic flows about dielectric surfaces of zero surface charge. Phys. Rev. E 89 (4), 043005.Google Scholar
Siddiqui, A. & Schwarz, W. 1994 Peristaltic flow of a second-order fluid in tubes. J. Non-Newtonian Fluid Mech. 53, 257–284.Google Scholar
Squires, T. M. & Bazant, M. Z. 2004 Induced-charge electro-osmosis. J. Fluid Mech. 509, 217–252.Google Scholar
Stroock, A. D. et al. 2000 Patterning electro-osmotic flow with patterned surface charge. Phys. Rev. Lett. 84 (15), 3314–3317.Google Scholar
Tanner, R. I. 1966 Plane creeping flows of incompressible second-order fluids. Phys. Fluids 9 (6), 1246–1247.Google Scholar
Thurston, G. B. & Griling, H. 1978 Viscoelastic properties of pathological synovial fluids for a wide range of oscillatory shear rates and frequencies. Rheol. Acta 445, 433–445.CrossRefGoogle Scholar
Vinogradova, O. I. & Belyaev, A. V. 2011 Wetting, roughness and flow boundary conditions. J. Phys.: Condens. Matter 23 (18), 184104.Google Scholar
Wang, X.-P., Qian, T. & Sheng, P. 2008 Moving contact line on chemically patterned surfaces. J. Fluid Mech. 605, 59–78.Google Scholar
Yang, Q., Li, B. Q. & Ding, Y. 2013 3D phase field modeling of electrohydrodynamic multiphase flows. Intl J. Multiphase Flow 57, 1–9.CrossRefGoogle Scholar
Yariv, E. 2004 Electro-osmotic flow near a surface charge discontinuity. J. Fluid Mech. 521, 181–189.Google Scholar
Yariv, E. 2009 An asymptotic derivation of the thin-Debye-layer limit for electrokinetic phenomena. Chem. Engng Commun. 197 (1), 3–17.Google Scholar
Yariv, E., Schnitzer, O. & Frankel, I. 2011 Streaming-potential phenomena in the thin-Debye-layer limit. Part 1. General theory. J. Fluid Mech. 685, 306–334.Google Scholar
Yeleswarapu, K. & Kameneva, M. 1998 The flow of blood in tubes: theory and experiment. Mech. Res. Commun. 25 (3), 257–262.Google Scholar
Zaltzman, B. & Rubinstein, I. 2007 Electro-osmotic slip and electroconvective instability. J. Fluid Mech. 579, 173.Google Scholar