Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-22T09:33:29.315Z Has data issue: false hasContentIssue false
  • English
  • Français

The energy flux spectrum of internal waves generated by turbulent convection

Published online by Cambridge University Press:  10 September 2018

Louis-Alexandre Couston Open the ORCID record for Louis-Alexandre Couston [Opens in a new window] ,
Daniel Lecoanet ,
Benjamin Favier Open the ORCID record for Benjamin Favier [Opens in a new window]  and
Michael Le Bars
Louis-Alexandre Couston*
Affiliation:
CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, Marseille, France
Daniel Lecoanet
Affiliation:
Princeton Center for Theoretical Science, Princeton, NJ 08544, USA
Benjamin Favier
Affiliation:
CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, Marseille, France
Michael Le Bars
Affiliation:
CNRS, Aix Marseille Univ, Centrale Marseille, IRPHE, Marseille, France
*
†Email address for correspondence: louisalexandre.couston@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We present three-dimensional direct numerical simulations of internal waves excited by turbulent convection in a self-consistent, Boussinesq and Cartesian model of mixed convective and stably stratified fluids. We demonstrate that in the limit of large Rayleigh number ($Ra\in [4\times 10^{7},10^{9}]$) and large stratification (Brunt–Väisälä frequencies 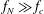$f_{N}\gg f_{c}$, where 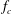$f_{c}$ is the convective frequency), simulations are in good agreement with a theory that assumes waves are generated by Reynolds stresses due to eddies in the turbulent region as described in Lecoanet & Quataert (Mon. Not. R. Astron. Soc., vol. 430 (3), 2013, pp. 2363–2376). Specifically, we demonstrate that the wave energy flux spectrum scales like 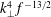$k_{\bot }^{4}\,f^{-13/2}$ for weakly damped waves (with 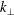$k_{\bot }$ and 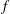$f$ the waves’ horizontal wavenumbers and frequencies, respectively), and that the total wave energy flux decays with $z$, the distance from the convective region, like $z^{-13/8}$.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Internal waves Turbulent Flows: Turbulent convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , R3
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A., Kawatani, Y., Pulido, M., Shaw, T. A., Sigmond, M., Vincent, R. & Watanabe, S. 2010 Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 136 (650), 1103–1124.Google Scholar
Ansong, J. K. & Sutherland, B. R. 2010 Internal gravity waves generated by convective plumes. J. Fluid Mech. 648, 405.Google Scholar
Bordes, G., Venaille, A., Joubaud, S., Odier, P. & Dauxois, T. 2012 Experimental observation of a strong mean flow induced by internal gravity waves. Phys. Fluids 24 (8), 086602.Google Scholar
van den Bremer, T. S. & Sutherland, B. R. 2018 The wave-induced flow of internal gravity wavepackets with arbitrary aspect ratio. J. Fluid Mech. 834, 385–408.Google Scholar
Burns, K. J., Vasil, G. M., Oishi, J. S., Lecoanet, D. & Brown, B. P. 2018 Dedalus: Flexible Framework for Spectrally Solving Differential Equations. Astrophysics Source Code Library.Google Scholar
Canet, L., Rossetto, V., Wschebor, N. & Balarac, G. 2017 Spatiotemporal velocity–velocity correlation function in fully developed turbulence. Phys. Rev. E 95, 023107.Google Scholar
Carruthers, D. J. & Hunt, J. C. R. 1986 Velocity fluctuations near an interface between a turbulent region and a stably stratified layer. J. Fluid Mech. 165, 475–501.Google Scholar
Chen, S. & Kraichnan, R. H. 1989 Sweeping decorrelation in isotropic turbulence. Phys. Fluids A 1 (12), 2019–2024.Google Scholar
Chevillard, L., Roux, S. G., Lévêque, E., Mordant, N., Pinton, J.-F. & Arnéodo, A. 2005 Intermittency of velocity time increments in turbulence. Phys. Rev. Lett. 95, 064501.Google Scholar
Couston, L.-A., Lecoanet, D., Favier, B. & Le Bars, M. 2017 Dynamics of mixed convective–stably-stratified fluids. Phys. Rev. Fluids 2, 094804.Google Scholar
Couston, L.-A., Lecoanet, D., Favier, B. & Le Bars, M. 2018 Order out of chaos: slowly reversing mean flows emerge from turbulently generated internal waves. Phys. Rev. Lett. 120, 244505.Google Scholar
Favier, B., Godeferd, F. S. & Cambon, C. 2010 On space and time correlations of isotropic and rotating turbulence. Phys. Fluids 22 (1), 015101.Google Scholar
Garaud, P. 2018 Double-diffusive convection at low Prandtl number. Annu. Rev. Fluid Mech. 50 (1), 275–298.Google Scholar
Goldreich, P. & Kumar, P. 1990 Wave generation by turbulent convection. Astrophys. J. 363, 694–704.Google Scholar
Grisouard, N. & Bühler, O. 2012 Forcing of oceanic mean flows by dissipating internal tides. J. Fluid Mech. 708, 250–278.Google Scholar
Kunze, E. 2017 Internal-wave-driven mixing: global geography and budgets. J. Phys. Oceanogr. 47 (6), 1325–1345.Google Scholar
Lecoanet, D., Le Bars, M., Burns, K. J., Vasil, G. M., Brown, B. P., Quataert, E. & Oishi, J. S. 2015 Numerical simulations of internal wave generation by convection in water. Phys. Rev. E 91 (6), 063016.Google Scholar
Lecoanet, D. & Quataert, E. 2013 Internal gravity wave excitation by turbulent convection. Mon. Not. R. Astron. Soc. 430 (3), 2363–2376.Google Scholar
Liot, O., Seychelles, F., Zonta, F., Chibbaro, S., Coudarchet, T., Gasteuil, Y., Pinton, J.-F., Salort, J. & Chillà, F. 2016 Simultaneous temperature and velocity Lagrangian measurements in turbulent thermal convection. J. Fluid Mech. 794, 655–675.Google Scholar
Munroe, J. R. & Sutherland, B. R. 2014 Internal wave energy radiated from a turbulent mixed layer. Phys. Fluids 26 (9), 096604.Google Scholar
Pinçon, C., Belkacem, K. & Goupil, M. J. 2016 Generation of internal gravity waves by penetrative convection. Astron. Astrophys. 588 (A122), 1–21.Google Scholar
Rogers, T. M., Lin, D. N. C. & Lau, H. H. B. 2012 Internal gravity waves modulate the apparent misalignment of exoplanets around hot stars. Astrophys. J. Lett. 758 (1), L6.Google Scholar
Rogers, T. M., Lin, D. N. C., McElwaine, J. N. & Lau, H. H. B. 2013 Internal gravity waves in massive stars: angular momentum transport. Astrophys. J. 772 (1), 21.Google Scholar
Sano, M., Wu, X. Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.Google Scholar
Staquet, C. & Sommeria, J. 2002 Internal gravity waves: from instabilities to turbulence. Annu. Rev. Fluid Mech. 34 (1), 559–593.Google Scholar
Taylor, J. R. & Sarkar, S. 2007 Internal gravity waves generated by a turbulent bottom Ekman layer. J. Fluid Mech. 590, 331–354.Google Scholar
Tennekes, H. 1975 Eulerian and Lagrangian time microscales in isotropic turbulence. J. Fluid Mech. 67 (3), 561–567.Google Scholar
Thorpe, S. A. 2018 Models of energy loss from internal waves breaking in the ocean. J. Fluid Mech. 836, 72–116.Google Scholar
Zhou, Y. & Rubinstein, R. 1996 Sweeping and straining effects in sound generation by high Reynolds number isotropic turbulence. Phys. Fluids 8 (3), 647–649.Google Scholar

Couston et al supplementary material

Movie of (a) $w(y = 0)$, (b) $T_z-\bar{T}_z$ at $y = 0$ (overbar denotes x average), (c) $w(z = 0.7)$, (d) $w(z = 1:3)$ for simulation case $C_8^{400}$. Variables in the wave region $(z > 1)$ in (a), (b) have been multiplied by $10^4$, $10^3$, respectively.

Download Couston et al supplementary material(Video)
Video 304 MB