Article contents
Energy spectra in turbulent bubbly flows
Published online by Cambridge University Press: 15 February 2016
Abstract
We conduct experiments in a turbulent bubbly flow to study the nature of the transition between the classical 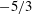 $-5/3$ energy spectrum scaling for a single-phase turbulent flow and the
$-5/3$ energy spectrum scaling for a single-phase turbulent flow and the 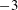 $-3$ scaling for a swarm of bubbles rising in a quiescent liquid and of bubble-dominated turbulence. The bubblance parameter (Lance & Bataille J. Fluid Mech., vol. 222, 1991, pp. 95–118; Rensen et al., J. Fluid Mech., vol. 538, 2005, pp. 153–187), which measures the ratio of the bubble-induced kinetic energy to the kinetic energy induced by the turbulent liquid fluctuations before bubble injection, is often used to characterise bubbly flow. We vary the bubblance parameter from
$-3$ scaling for a swarm of bubbles rising in a quiescent liquid and of bubble-dominated turbulence. The bubblance parameter (Lance & Bataille J. Fluid Mech., vol. 222, 1991, pp. 95–118; Rensen et al., J. Fluid Mech., vol. 538, 2005, pp. 153–187), which measures the ratio of the bubble-induced kinetic energy to the kinetic energy induced by the turbulent liquid fluctuations before bubble injection, is often used to characterise bubbly flow. We vary the bubblance parameter from 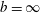 $b=\infty$ (pseudoturbulence) to
$b=\infty$ (pseudoturbulence) to 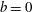 $b=0$ (single-phase flow) over 2–3 orders of magnitude (0.01–5) to study its effect on the turbulent energy spectrum and fluctuations in liquid velocity. The probability density functions (PDFs) of the fluctuations in liquid velocity show deviations from the Gaussian profile for
$b=0$ (single-phase flow) over 2–3 orders of magnitude (0.01–5) to study its effect on the turbulent energy spectrum and fluctuations in liquid velocity. The probability density functions (PDFs) of the fluctuations in liquid velocity show deviations from the Gaussian profile for 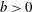 $b>0$ , i.e. when bubbles are present in the system. The PDFs are asymmetric with higher probability in the positive tails. The energy spectra are found to follow the
$b>0$ , i.e. when bubbles are present in the system. The PDFs are asymmetric with higher probability in the positive tails. The energy spectra are found to follow the 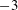 $-3$ scaling at length scales smaller than the size of the bubbles for bubbly flows. This
$-3$ scaling at length scales smaller than the size of the bubbles for bubbly flows. This 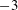 $-3$ spectrum scaling holds not only in the well-established case of pseudoturbulence, but surprisingly in all cases where bubbles are present in the system (
$-3$ spectrum scaling holds not only in the well-established case of pseudoturbulence, but surprisingly in all cases where bubbles are present in the system ( 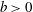 $b>0$ ). Therefore, it is a generic feature of turbulent bubbly flows, and the bubblance parameter is probably not a suitable parameter to characterise the energy spectrum in bubbly turbulent flows. The physical reason is that the energy input by the bubbles passes over only to higher wavenumbers, and the energy production due to the bubbles can be directly balanced by the viscous dissipation in the bubble wakes as suggested by Lance & Bataille (1991). In addition, we provide an alternative explanation by balancing the energy production of the bubbles with viscous dissipation in the Fourier space.
$b>0$ ). Therefore, it is a generic feature of turbulent bubbly flows, and the bubblance parameter is probably not a suitable parameter to characterise the energy spectrum in bubbly turbulent flows. The physical reason is that the energy input by the bubbles passes over only to higher wavenumbers, and the energy production due to the bubbles can be directly balanced by the viscous dissipation in the bubble wakes as suggested by Lance & Bataille (1991). In addition, we provide an alternative explanation by balancing the energy production of the bubbles with viscous dissipation in the Fourier space.
Information
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 79
- Cited by


