Article contents
Entry and exit flows in curved pipes
Published online by Cambridge University Press: 23 February 2017
Abstract
Solutions are presented for both laminar developing flow in a curved pipe with a parabolic inlet velocity and laminar transitional flow downstream of a curved pipe into a straight outlet. Scalings and linearized analyses about appropriate base states are used to show that both cases obey the same governing equations and boundary conditions. In particular, the governing equations in the two cases are linearized about fully developed Poiseuille flow in cylindrical coordinates and about Dean’s velocity profile for curved pipe flow in toroidal coordinates respectively. Subsequently, we identify appropriate scalings of the axial coordinate and disturbance velocities that eliminate dependence on the Reynolds number 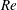 $Re$ and dimensionless pipe curvature
$Re$ and dimensionless pipe curvature  $\unicode[STIX]{x1D6FC}$ from the governing equations and boundary conditions in the limit of small
$\unicode[STIX]{x1D6FC}$ from the governing equations and boundary conditions in the limit of small  $\unicode[STIX]{x1D6FC}$ and large
$\unicode[STIX]{x1D6FC}$ and large 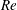 $Re$ . Direct numerical simulations confirm the scaling arguments and theoretical solutions for a range of
$Re$ . Direct numerical simulations confirm the scaling arguments and theoretical solutions for a range of 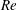 $Re$ and
$Re$ and  $\unicode[STIX]{x1D6FC}$ . Maximum values of the axial velocity, secondary velocity and pressure perturbations are determined along the curved pipe section. Results collapse when the scalings are applied, and the theoretical solutions are shown to be valid up to Dean numbers of
$\unicode[STIX]{x1D6FC}$ . Maximum values of the axial velocity, secondary velocity and pressure perturbations are determined along the curved pipe section. Results collapse when the scalings are applied, and the theoretical solutions are shown to be valid up to Dean numbers of 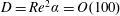 $D=Re^{2}\unicode[STIX]{x1D6FC}=O(100)$ . The developing flows are shown numerically and analytically to contain spatial oscillations. The numerically determined decay of the velocity perturbations is also used to determine entrance/development lengths for both flows, which are shown to scale linearly with the Reynolds number, but with a prefactor
$D=Re^{2}\unicode[STIX]{x1D6FC}=O(100)$ . The developing flows are shown numerically and analytically to contain spatial oscillations. The numerically determined decay of the velocity perturbations is also used to determine entrance/development lengths for both flows, which are shown to scale linearly with the Reynolds number, but with a prefactor 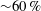 ${\sim}60\,\%$ larger than the textbook case of developing flow in a straight pipe.
${\sim}60\,\%$ larger than the textbook case of developing flow in a straight pipe.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 14
- Cited by


