Article contents
Estimating large-scale structures in wall turbulence using linear models
Published online by Cambridge University Press: 06 March 2018
Abstract
A dynamical systems approach is used to devise a linear estimation tool for channel flow at a friction Reynolds number of 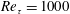 $Re_{\unicode[STIX]{x1D70F}}=1000$ . The estimator uses time-resolved velocity measurements at a single wall-normal location to estimate the velocity field at other wall-normal locations (the data coming from direct numerical simulations). The estimation tool builds on the work of McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) by using a Navier–Stokes-based linear model and treating any nonlinear terms as unknown forcings to an otherwise linear system. In this way nonlinearities are not ignored, but instead treated as an unknown model input. It is shown that, while the linear estimator qualitatively reproduces large-scale flow features, it tends to overpredict the amplitude of velocity fluctuations – particularly for structures that are long in the streamwise direction and thin in the spanwise direction. An alternative linear model is therefore formed in which a simple eddy viscosity is used to model the influence of the small-scale turbulent fluctuations on the large scales of interest. This modification improves the estimator performance significantly. Importantly, as well as improving the performance of the estimator, the linear model with eddy viscosity is also able to predict with reasonable accuracy the range of wavenumber pairs and the range of wall-normal heights over which the estimator will perform well.
$Re_{\unicode[STIX]{x1D70F}}=1000$ . The estimator uses time-resolved velocity measurements at a single wall-normal location to estimate the velocity field at other wall-normal locations (the data coming from direct numerical simulations). The estimation tool builds on the work of McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) by using a Navier–Stokes-based linear model and treating any nonlinear terms as unknown forcings to an otherwise linear system. In this way nonlinearities are not ignored, but instead treated as an unknown model input. It is shown that, while the linear estimator qualitatively reproduces large-scale flow features, it tends to overpredict the amplitude of velocity fluctuations – particularly for structures that are long in the streamwise direction and thin in the spanwise direction. An alternative linear model is therefore formed in which a simple eddy viscosity is used to model the influence of the small-scale turbulent fluctuations on the large scales of interest. This modification improves the estimator performance significantly. Importantly, as well as improving the performance of the estimator, the linear model with eddy viscosity is also able to predict with reasonable accuracy the range of wavenumber pairs and the range of wall-normal heights over which the estimator will perform well.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Illingworth et al. supplementary movie 1
Estimation of the streamwise velocity perturbation at $z^+=101$ using the linear model \eqref{eq:lm1}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).
Illingworth et al. supplementary movie 2
Estimation of the streamwise velocity perturbation at $z^+=297$ using the linear model \eqref{eq:lm1}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).
Illingworth et al. supplementary movie 3
Estimation of the streamwise velocity perturbation at $z^+=101$ using the linear model \eqref{eq:lm2}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).
Illingworth et al. supplementary movie 4
Estimation of the streamwise velocity perturbation at $z^+=297$ using the linear model \eqref{eq:lm2}: (\textit{a}) DNS data; and (\textit{b}) linear estimate using measurements at $z^+=197$; (\textit{c}) time history at $x=\pi/2$, $y=\pi/2$ for the DNS data (---) and for the linear estimate (-\,-). Sixty-five contour levels are shown from $u=-3.5$ (blue) to $u=+3.5$ (red).
- 89
- Cited by


