Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tritschler, V. K.
Olson, B. J.
Lele, S. K.
Hickel, S.
Hu, X. Y.
and
Adams, N. A.
2014.
On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface.
Journal of Fluid Mechanics,
Vol. 755,
Issue. ,
p.
429.
Weber, Christopher R.
Haehn, Nicholas S.
Oakley, Jason G.
Rothamer, David A.
and
Bonazza, Riccardo
2014.
An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability.
Journal of Fluid Mechanics,
Vol. 748,
Issue. ,
p.
457.
Zhai, Zhigang
Wang, Minghu
Si, Ting
and
Luo, Xisheng
2014.
On the interaction of a planar shock with a light polygonal interface.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
800.
McFarland, Jacob A.
Reilly, David
Black, Wolfgang
Greenough, Jeffrey A.
and
Ranjan, Devesh
2015.
Modal interactions between a large-wavelength inclined interface and small-wavelength multimode perturbations in a Richtmyer-Meshkov instability.
Physical Review E,
Vol. 92,
Issue. 1,
Gerashchenko, S.
and
Prestridge, K.
2015.
Density and velocity statistics in variable density turbulent mixing.
Journal of Turbulence,
Vol. 16,
Issue. 11,
p.
1011.
Nelson, Nicholas J.
and
Grinstein, Fernando F.
2015.
Effects of initial condition spectral content on shock-driven turbulent mixing.
Physical Review E,
Vol. 92,
Issue. 1,
Orlicz, G. C.
Balasubramanian, Sridhar
Vorobieff, P.
and
Prestridge, K. P.
2015.
Mixing transition in a shocked variable-density flow.
Physics of Fluids,
Vol. 27,
Issue. 11,
Luo, Xisheng
Wang, Minghu
Si, Ting
and
Zhai, Zhigang
2015.
On the interaction of a planar shock with an polygon.
Journal of Fluid Mechanics,
Vol. 773,
Issue. ,
p.
366.
Zou, Liyong
Liao, Shenfei
Liu, Cangli
Wang, Yanping
and
Zhai, Zhigang
2016.
Aspect ratio effect on shock-accelerated elliptic gas cylinders.
Physics of Fluids,
Vol. 28,
Issue. 3,
Luo, Xisheng
Dong, Ping
Si, Ting
and
Zhai, Zhigang
2016.
The Richtmyer–Meshkov instability of a ‘V’ shaped air/ interface.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
186.
Zhai, Zhigang
Dong, Ping
Si, Ting
and
Luo, Xisheng
2016.
The Richtmyer-Meshkov instability of a “V” shaped air/helium interface subjected to a weak shock.
Physics of Fluids,
Vol. 28,
Issue. 8,
Black, Wolfgang J.
Denissen, Nicholas A.
and
McFarland, Jacob A.
2017.
Evaporation Effects in Shock-Driven Multiphase Instabilities.
Journal of Fluids Engineering,
Vol. 139,
Issue. 7,
Gao, Fujie
Zhang, Yousheng
He, Zhiwei
Li, Li
and
Tian, Baolin
2017.
Characteristics of turbulent mixing at late stage of the Richtmyer-Meshkov instability.
AIP Advances,
Vol. 7,
Issue. 7,
Ding, Juchun
Si, Ting
Chen, Mojun
Zhai, Zhigang
Lu, Xiyun
and
Luo, Xisheng
2017.
On the interaction of a planar shock with a three-dimensional light gas cylinder.
Journal of Fluid Mechanics,
Vol. 828,
Issue. ,
p.
289.
Zhou, Ye
2017.
Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II.
Physics Reports,
Vol. 723-725,
Issue. ,
p.
1.
Wang, Tao
Tao, Gang
Bai, Jingsong
Li, Ping
Wang, Bing
Du, Lei
and
Xiao, Jiaxin
2017.
Dynamical behavior of the Richtmyer–Meshkov instability-induced turbulent mixing under multiple shock interactions.
Canadian Journal of Physics,
Vol. 95,
Issue. 8,
p.
671.
Mohaghar, Mohammad
Carter, John
Musci, Benjamin
Reilly, David
McFarland, Jacob
and
Ranjan, Devesh
2017.
Evaluation of turbulent mixing transition in a shock-driven variable-density flow.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
779.
Zeng, Wei-Gang
Pan, Jian-Hua
Sun, Yu-Tao
and
Ren, Yu-Xin
2018.
Turbulent mixing and energy transfer of reshocked heavy gas curtain.
Physics of Fluids,
Vol. 30,
Issue. 6,
Ding, Juchun
Liang, Yu
Chen, Mojun
Zhai, Zhigang
Si, Ting
and
Luo, Xisheng
2018.
Interaction of planar shock wave with three-dimensional heavy cylindrical bubble.
Physics of Fluids,
Vol. 30,
Issue. 10,
Prestridge, Kathy
2018.
Experimental adventures in variable-density mixing.
Physical Review Fluids,
Vol. 3,
Issue. 11,
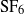 ${\mathrm{SF} }_{6} $ –air) fluid layer subjected to a shock (Mach 1.20) and a reshock (Mach 1.14) is investigated using ensemble statistics obtained from simultaneous velocity–density measurements. The mixing is driven by an unstable array of initially symmetric vortices that induce rapid material mixing and create smaller-scale vortices. After reshock the flow appears to transition to a turbulent (likely three-dimensional) state, at which time our planar measurements are used to probe the developing flow field. The density self-correlation
${\mathrm{SF} }_{6} $ –air) fluid layer subjected to a shock (Mach 1.20) and a reshock (Mach 1.14) is investigated using ensemble statistics obtained from simultaneous velocity–density measurements. The mixing is driven by an unstable array of initially symmetric vortices that induce rapid material mixing and create smaller-scale vortices. After reshock the flow appears to transition to a turbulent (likely three-dimensional) state, at which time our planar measurements are used to probe the developing flow field. The density self-correlation 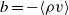 $b= - \langle \rho v\rangle $ (where
$b= - \langle \rho v\rangle $ (where 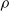 $\rho $ and
$\rho $ and  $v$ are the fluctuating density and specific volume, respectively) and terms in its evolution equation are directly measured experimentally for the first time. Amongst other things, it is found that production terms in the
$v$ are the fluctuating density and specific volume, respectively) and terms in its evolution equation are directly measured experimentally for the first time. Amongst other things, it is found that production terms in the 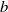 $b$ equation are balanced by the dissipation terms, suggesting a form of equilibrium in
$b$ equation are balanced by the dissipation terms, suggesting a form of equilibrium in 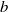 $b$ . Simultaneous velocity measurements are used to probe the state of the incipient turbulence. A length-scale analysis suggests that an inertial range is beginning to form, consistent with the onset of a mixing transition. The developing turbulence is observed to reduce non-Boussinesq effects in the flow, which are found to be small over much of the layer after reshock. Second-order two-point structure functions of the density field exhibit a power-law behaviour with a steeper exponent than the standard
$b$ . Simultaneous velocity measurements are used to probe the state of the incipient turbulence. A length-scale analysis suggests that an inertial range is beginning to form, consistent with the onset of a mixing transition. The developing turbulence is observed to reduce non-Boussinesq effects in the flow, which are found to be small over much of the layer after reshock. Second-order two-point structure functions of the density field exhibit a power-law behaviour with a steeper exponent than the standard 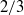 $2/ 3$ power found in canonical turbulence. The absence of a significant
$2/ 3$ power found in canonical turbulence. The absence of a significant 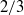 $2/ 3$ region is observed to be consistent with the state of the flow, and the emergence of the steeper power-law region is discussed.
$2/ 3$ region is observed to be consistent with the state of the flow, and the emergence of the steeper power-law region is discussed.
