Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Wu, H.
Moreau, S.
and
Sandberg, R. D.
2019.
Effects of pressure gradient on the evolution of velocity-gradient tensor invariant dynamics on a controlled-diffusion aerofoil at .
Journal of Fluid Mechanics,
Vol. 868,
Issue. ,
p.
584.
Yu, Jia-Long
and
Lu, Xi-Yun
2019.
Topological evolution near the turbulent/non-turbulent interface in turbulent mixing layer.
Journal of Turbulence,
Vol. 20,
Issue. 5,
p.
300.
Tian, Yifeng
Jaberi, Farhad A.
and
Livescu, Daniel
2019.
Density effects on post-shock turbulence structure and dynamics.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
935.
Sharma, S.
Shadloo, M.S.
and
Hadjadj, A.
2019.
Turbulent flow topology in supersonic boundary layer with wall heat transfer.
International Journal of Heat and Fluid Flow,
Vol. 78,
Issue. ,
p.
108430.
Parashar, Nishant
Sinha, Sawan Suman
and
Srinivasan, Balaji
2019.
Lagrangian investigations of velocity gradients in compressible turbulence: lifetime of flow-field topologies.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
492.
Wang, Jianchun
Wan, Minping
Chen, Song
Xie, Chenyue
Zheng, Qinmin
Wang, Lian-Ping
and
Chen, Shiyi
2020.
Effect of flow topology on the kinetic energy flux in compressible isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 883,
Issue. ,
Das, Rishita
and
Girimaji, Sharath S.
2020.
Characterization of velocity-gradient dynamics in incompressible turbulence using local streamline geometry.
Journal of Fluid Mechanics,
Vol. 895,
Issue. ,
Yu, Jia-Long
and
Lu, Xi-Yun
2020.
Subgrid effects on the filtered velocity gradient dynamics in compressible turbulence.
Journal of Fluid Mechanics,
Vol. 892,
Issue. ,
Tian, Yifeng
Livescu, Daniel
and
Chertkov, Michael
2021.
Physics-informed machine learning of the Lagrangian dynamics of velocity gradient tensor.
Physical Review Fluids,
Vol. 6,
Issue. 9,
Yu, Jia-Long
Zhao, Zhiye
and
Lu, Xi-Yun
2021.
Non-normal effect of the velocity gradient tensor and the relevant subgrid-scale model in compressible turbulent boundary layer.
Physics of Fluids,
Vol. 33,
Issue. 2,
Xu, Dehao
Wang, Jianchun
Yu, Changping
Li, Xinliang
and
Chen, Shiyi
2022.
Effect of compressibility on the small-scale structures in hypersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 5,
Das, Rishita
and
Girimaji, Sharath S.
2022.
The effect of large-scale forcing on small-scale dynamics of incompressible turbulence.
Journal of Fluid Mechanics,
Vol. 941,
Issue. ,
Xu, Dehao
Wang, Jianchun
Yu, Changping
Li, Xinliang
and
Chen, Shiyi
2022.
Contribution of flow topology to the kinetic energy flux in hypersonic turbulent boundary layer.
Physics of Fluids,
Vol. 34,
Issue. 4,
Tang, Jiu-Peng
Wan, Zhen-Hua
Liu, Nan-Sheng
and
Lu, Xi-Yun
2022.
Statistical properties of pressure-Hessian tensor in a turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Wu, Geyi
and
Xu, Chunxiao
2024.
Characterization and evolution of local streamline geometry in an incompressible turbulent channel flow.
Physics of Fluids,
Vol. 36,
Issue. 2,
Baj, Pawel
2024.
The topology-conditioned turbulence kinetic energy budget.
Physics of Fluids,
Vol. 36,
Issue. 9,
Onofre Ramos, Marcos M.
Bouali, Zakaria
and
Mura, Arnaud
2024.
Turbulence topology evolution in weakly turbulent two-phase flows.
Physics of Fluids,
Vol. 36,
Issue. 1,
Lilly, Jonathan M.
Feske, Joel
Fox-Kemper, Baylor
and
Early, Jeffrey J.
2024.
Integral theorems for the gradient of a vector field, with a fluid dynamical application.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 480,
Issue. 2293,
Zhao, Zhiye
Fu, Lin
and
Lu, Xi-Yun
2025.
Principal invariants of acceleration gradient tensor and their statistics in compressible channel flow.
Physical Review Fluids,
Vol. 10,
Issue. 6,
Bilbao-Ludena, Juan Carlos
and
Papadakis, George
2025.
Non-normality and small-scale statistics in a three-dimensional, separated shear flow.
Journal of Fluid Mechanics,
Vol. 1010,
Issue. ,
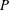 $P$ ,
$P$ , 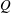 $Q$ and
$Q$ and 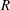 $R$ of the velocity gradient tensor have been derived. The mean evolution of characteristic turbulent structure types in the
$R$ of the velocity gradient tensor have been derived. The mean evolution of characteristic turbulent structure types in the 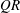 $QR$ -space were studied and compared at different wall-normal locations of a compressible turbulent boundary layer. The evolution of these structure types is fundamental to the physics that needs to be captured by turbulence models. Significant variations of the mean evolution are found across the boundary layer. The key features of the changes of the mean trajectories in the invariant phase space are highlighted and the consequences of the changes are discussed. Further, the individual elements of the overall evolution are studied separately to identify the causes that lead to the evolution varying with the distance to the wall. Significant impact of the wall-normal location on the coupling between the pressure-Hessian tensor and the velocity gradient tensor was found. The highlighted features are crucial for the development of more universal future turbulence models.
$QR$ -space were studied and compared at different wall-normal locations of a compressible turbulent boundary layer. The evolution of these structure types is fundamental to the physics that needs to be captured by turbulence models. Significant variations of the mean evolution are found across the boundary layer. The key features of the changes of the mean trajectories in the invariant phase space are highlighted and the consequences of the changes are discussed. Further, the individual elements of the overall evolution are studied separately to identify the causes that lead to the evolution varying with the distance to the wall. Significant impact of the wall-normal location on the coupling between the pressure-Hessian tensor and the velocity gradient tensor was found. The highlighted features are crucial for the development of more universal future turbulence models.

